|
|
|
Après avoir rappelé la lente progression à travers l’histoire des connaissances de la chimie et de son aboutissement à la théorie atomique on peut maintenant mieux comprendre et aborder l’application concrète de cette dernière. Parce qu’historiquement, l’étude du comportement des gaz (comportement physique) a participé à la compréhension de la matière et donc à l’affinement de la théorie atomique, il est normal d’aborder l’étude de la matière par l’étude des gaz. On verra aussi que le milieu gazeux permet une théorisation relativement poussée de ses comportements. Quelles sont donc les lois qui gouvernent ou rendent compte du comportement des gaz ? Pour commencer on abordera les comportements des gaz dits idéaux, repoussant au chapitre suivant l’étude des gaz réels. Objectif: connaître les lois qui gouvernent le comportements des systèmes gazeux dans une situation simple, ou mieux idéale.
|
1.1. La loi de BOYLE-MARIOTTE
D’une manière générale, le volume d’un gaz dépend de plusieurs paramètres au nombre desquels on peut identifier la quantité qu’on traduira par le nombre de mole n, la température T et la pression P. Historiquement, le baromètre à mercure a été inventé par Evangelista TORRICELLI en 1643. Il remarquât que la pression atmosphérique variait de quelques centimètres d’un jour à l’autre. On sait maintenant que dans des conditions dites standards qui seront précisées ultérieurement, 1 atmosphère est égal à 101 325 N/m2. On utilise aussi le bar qui est égal à 105 N/m2, donc un tout petit moins qu’un atmosphère. À basse pression on utilise souvent le mm de Hg (mmHg) qui fut aussi appelé le «torr» en l’honneur de TORRICELLI. Il vaut 1/760e d’une atmosphère.
En 1660, Boyle publia le résultats de ses observations. Il avait construit une pompe à vide. Notons au passage qu’en ces moments où la notion de vide faisait son apparition, certains philosophes prétendaient démontrer que le vide ne pouvait exister : « Le vide est rien et ce qui est rien ne peut exister ». En modifiant quelque peu son approche expérimentale, en 1662, BOYLE en arrivait à démontrer que le produit Pression ´ Volume est constant : le volume d’un échantillon gazeux est inversement proportionnel à sa pression. En termes mathématiques, P µ 1 / V, ce qu’exprime la figure 2.1 :
2.1 P V = Constante
|
|
Figure
2.1. Relation pression – volume pour un gaz idéal.
n1 et n2 sont des quantités différentes de
gaz.
Remarquons que la courbe P = f(V) est analytiquement une hyperbole (Fig. 2.1). Expérimentalement, il n’est pas évident, à la simple observation de la courbe, que c’est une hyperbole. Le tracé des courbes correspondantes P = f(1/V) (Fig. 2.2), ou encore celui de PV = f(P) (Fig. 2.3), est plus éloquent quant à la réelle relation entre la pression P et le volume V.
|
|
Figure 2.2. Relation pression – inverse du volume pour un gaz idéal.
|
|
Figure 2.3. Relation entre le produit PV et la pression pour un gaz idéal.
Notons que si l’on change de pression, on aura toujours :
P1 V1
= P2 V2
= P3 V3
= …
= PN VN
BOYLE avait aussi noté que le changement de température avait aussi un effet sur le produit PV. Il n’alla cependant pas plus loin dans ses observations. C’est en 1676 que MARIOTTE compléta la loi de BOYLE en ajoutant à température constante. D’où la loi de BOYLE MARIOTTE.
1.2.
La loi de GAY-LUSSAC
GAY-LUSSAC devait montrer que pour un volume fixe contenant une quantité elle aussi fixe de gaz, la pression du gaz est proportionnelle à la température de ce gaz (Fig. 2.4). De plus ce coefficient k est le même pour tous les gaz :
P = k T
k est un coefficient de proportionnalité.
|
|
Figure 2.4. Relation pression – température pour un gaz idéal.
Notons que si la température tend vers zéro, le volume tend aussi vers zéro. Cette observation est à la base de la mesure de la température du zéro absolu. En introduisant une certaine quantité de gaz dans un ballon et en le refroidissant on mesure le volume à diverses températures. Par extrapolation vers le volume nul, on obtient cette valeur du zéro absolu : -273,15 °C.
1.3.
La loi de CHARLES
En fait, CHARLES découvrit à peu près la même chose quinze ans plutôt mais ne publia pas ses résultats. Il montrait qu’à pression constante le volume d’une quantité déterminée de gaz est proportionnel à la température exprimée en kelvin (Fig. 2.5) :
V = k' T
Dans cette équation, k' est un coefficient de proportionnalité.
|
|
Figure 2.5. Relation pression – température pour un gaz idéal.
1.4. La Loi de CHARLES et GAY-LUSSAC
L’augmentation de volume d’un gaz en fonction de la température est donnée par la relation :
V = V0 (1 + a t)
V est le volume d’une quantité de gaz à pression constante ; V0 est le volume de cette même quantité de gaz à la température de 0 ºC ; t est la température en ºC et a une constante.
1.5. La combinaison de ces lois
Pour un échantillon gazeux, la combinaison des différentes lois ci-haut présentées s’écrit sous la forme suivante :
| 2.2 |
|
Pour un échantillon gazeux contenant un nombre n moles, le rapport PV/T est constant quelles que soient les valeurs de la pression, du volume et de la température. En d’autres termes, si l’on fixe arbitrairement 2 de ces trois paramètres, le troisième prend automatiquement la valeur appropriée pour satisfaire l’équation.
Comme, par ailleurs, la nature du gaz
n’intervient pas dans aucune des relations précédentes, la relation 2.2 est
vraie pourvu que n garde la même valeur.
2. Définition
Avant d’essayer d’établir théoriquement certaines propriétés d’un gaz, on doit définir les éléments de base de ce qu’est un gaz idéal. Afin de minimiser les complications de toutes sortes, on établira les propriétés de base d’un gaz idéal de la manière suivante :
1- Le volume des molécules est négligeable devant le volume total du réacteur ;
2- Ces molécules sont des sphères rigides infiniment petites ;
3- Elles ont une masse m ;
4- Il n’existe aucune attraction, répulsion, de manière générale aucune interaction, entre les molécules autrement que les collisions qui peuvent survenir ;
5- Il en est de même des interactions entre les molécules et les parois du réacteur qui les contiennent.
6- On suppose que ces molécules sont en mouvement, mouvement pour le moment désordonné, appelé mouvement brownien.
3. La théorie cinétique des gaz
Soit un contenant cubique de côté a. La vitesse c d’une molécule peut être décomposée sur chacun des trois Ox, Oy et Oz du trièdre trirectangle, de telle sorte que :
| 2.3 |
|
En utilisant le théorème de PYTHAGORE, le carré de la vitesse est égal à la somme des carrés des composantes de la vitesse sur chacun des trois axes :
2.4
c2
= cx2
+ cy2
+ cz
3.1.
Calcul de la pression exercée sur les parois du réacteur
Les molécules en mouvement frappent les parois du réacteur et sont ainsi la cause de la pression du contenu sur le contenant. Supposons que les chocs sur ces parois sont élastiques. C’est-à-dire que l’angle d’incidence de la collision est égal à l’angle de réflexion. La vitesse change de sens mais non de grandeur. Seule la quantité de mouvement change de signe (Fig. 2.6).
| 2.5
|
|
|
|
Figure 2.6. Collision d’une molécule sur les parois d’un réacteur.
Le nombre de collision par unité de temps (sur la surface perpendiculaire à la direction Ox) est égal à cx / a. Ainsi la variation de la quantité de mouvement par unité de temps est alors :
2.6 2 m cx ( cx / a ) = 2 m cx2 / a
Il faut en effet remarquer qu’à chaque collision avec la paroi, la variation de la quantité de mouvement est égale à 2 m cx. S’il y a N molécules, la variation de la quantité de mouvement par unité de temps est donnée par la relation :
| 2.7 |
|
Dans cette expression le carré de la vitesse selon l’axe
des Ox, surmonté d’un trait horizontal, représente la moyenne du carré
des vitesses de N particules. On ne
peut en effet supposer que toutes les N molécules se déplacent à la même
vitesse. En accordant la vitesse cxi
à la ie particule, l’équation 2.5 peut se réécrire :
| 2.8 |
|
Ainsi :
| 2.9 |
|
Il apparaît
ainsi que M, le changement de la de la quantité de mouvement par unité de
temps (la vitesse de changement de la quantité de mouvement) est la seule force
exercée sur les parois du contenant perpendiculaires à la direction Ox
et dont la surface est égale à 2 a2.
En se souvenant
que le rapport d’une quantité de mouvement divisé par une surface est égal
à une pression, on obtient :
|
2.10 |
|
Dans cette équation V est le volume du réacteur. Comme on ne peut distinguer cx2 de cy2 et de cz2, on peut généraliser l’équation 2.8 :
| 2.11 |
|
avec,
| 2.12 |
|
Note : On
définira un peu plus tard la vitesse quadratique moyenne qui est différente de
la moyenne du carré de la vitesse tout juste exprimée.
3.2.
Calcul de l’énergie cinétique des particules
L’énergie de translation ET des molécules est :
2.13
ET =
1/2 m
(c12 + c22 + c32 + … +
ci2
+ …
cN2)
| 2.14 |
|
Or d’après
l’équation 2.11,
| 2.15 |
|
Cette énergie est constante, inchangée par les collisions sur les parois. En effet, si à l’échelle moléculaire il y a échange d’énergie avec les molécules (hypothèse de collisions non élastiques), à l’échelle macroscopique, à température constante, l’énergie de l’ensemble des molécules demeure constante. Cette équation 2.15 est équivalente à la loi de BOYLE – MARIOTTE.
3.3. Énergie cinétique et température
La température d’un échantillon gazeux est une fonction de l’énergie de translation seule :
T =
f(ET)
De plus cette
fonction doit avoir la forme suivante :
| 2.16 |
|
de
telle sorte que
l’équation 2.15 soit en accord avec l’équation P V
= n R T. Ainsi la température T est proportionnelle à l’énergie
de translation des molécules. À zéro
kelvin, toutes les molécules seront fixes, c’est-à-dire sans énergie de
translation. Si l’énergie totale
est égale à l’énergie de translation, alors :
2.17 E = ET = (3/2) n R T
Définissons la
capacité calorifique molaire à volume constant : elle correspond à la
quantité d’énergie essentiellement sous forme cinétique que la mole de gaz est capable d’emmagasiner
lorsque la température du gaz augmente de 1 º.
En termes mathématiques, la capacité calorifique d’un gaz correspond
à la dérivée de l’énergie de translation sans changement de volume.
| 2.18 |
|
Ainsi, on
montrera ultérieurement que cela est bien le cas pour l’hélium et l’argon.
Si la capacité calorifique molaire à volume constant observée est
supérieure à celle calculée à l’aide de la relation 2.18, il faudra
admettre que la molécule peut absorber de l’énergie sous d’autres formes
que la seule énergie de translation.
L’énergie de
translation peut-être distribuée dans les trois directions possibles du trièdre
trirectangle. Ainsi, en écrivant
le nombre d’AVOGADRO par
N, et en combinant les équations
2.12 et 2.14, on
obtient :
| 2.19
|
|
Avec la relation 2.17 :
| 2.20 |
|
Comme les trois
axes du trièdre trirectangle sont indiscernables, pour chacun des trois degrés
de liberté de translation, on obtient :
| 2.21 |
|
par degré de liberté |
3.4. Vitesses moléculaires
La relation 2.15 peut s’écrire :
| 2.22 |
|
Le rapport Nm
/ V est identique à une densité (masse/volume) : c’est la densité r
du gaz.
| 2.23 |
|
En combinant ce résultat avec les équations 2.17 et 2.19, cette équation devient :
| 2.24 |
|
(pour trois degrés de liberté) |
Si M est la masse molaire du gaz, le produit A m est égal à M :
| 2.25 |
|
On obtient
ainsi la racine carrée de la moyenne du carré de la vitesse :
| 2.26 |
|
Cette
expression est appelée la vitesse quadratique moyenne.
On verra plus tard que la moyenne de la vitesse est différente :
| 2.27 |
|
Comme le
rapport 8/p est inférieur à 3,
| Þ |
|
Tableau
2.1. Exemples de moyennes de
vitesses et de vitesses quadratiques moyennes
à la température de 300 K
| Gaz |
|
|
Gaz |
|
|
| H2 |
1785 |
1940 |
He | 1259 |
1368 |
| D2 |
1259 |
1368 |
CH4 | 638 |
693 |
| N2 |
478 |
520 |
H2O |
590 |
641 |
| O2 |
446 |
485 |
iso-C4H8 | 335 |
364 |
3.5. Collisions entre molécules
Soit une molécule, une sphère rigide, de diamètre d animée d’une vitesse c. Il y aura collision lorsque le centre d’une autre molécule sera aussi proche d’une distance d d’une autre molécule. Toutes les molécules qui se trouvent dans le cylindre de révolution situé autour du vecteur c seront frappées par cette molécule (Fig. 2.7). Puisqu’il y a N molécules / cm3, le nombre de collisions Z1 engendrées par cette molécule est donné par :
![]()
|
|
Figure 2.7. Collision d’une molécule en mouvement avec les autres particules du gaz.
Un calcul plus exact faisant intervenir les vitesses relatives des molécules conduit à :
![]()
Ce nombre correspond au nombre de collision d’une molécule avec les autres par unité de temps. Si l’on calcule l’ensemble de des collisions engendrées par toutes les molécules, il faut multiplier ce nombre par N en n’oubliant pas de diviser par deux puisqu’une collision de A avec B est identique à la collision de B avec A.
| 2.28 |
|
Rappelons que
la vitesse moyenne dépend de la racine carrée de la température ; équation
2.27. Il en est donc de même de la
vitesse de collision.
3.6.
Le libre parcours moyen
Le libre parcours moyen l est la distance moyenne parcourue par une molécule entre deux collisions
|
|
|
Ce qui en combinant les équations 2.27 et 2.28 conduit à :
| 2.30 |
|
Il est donc essentiel de connaître le diamètre moyen des molécules. On verra dans les prochains chapitres au moins une méthode de détermination de ce diamètre moléculaire moyen à travers la loi de VAN DER WAALS. La diffraction des rayons X et la spectroscopie micro-onde sont aussi des méthodes très puissantes (voir un cours de cristallographie par exemple) ou un cours de spectroscopie approprié (chapitre 3 du cours de chimie théorique). Les équations de diffusion des gaz et la viscosimétrie permettent aussi d’obtenir des valeurs très appropriées. Inutile de rappeler qu’un bon chimiste doit pouvoir se servir d’un Handbook de chimie et qu’il trouvera là beaucoup d’informations.
3.7.
La loi de BOLTZMANN - La
distribution de BOLTZMANN
Si N0 est le nombre de molécules (particules) dans un état donné, le Nombre Ni dont l’énergie potentielle est ei est donné par la relation :
Ni
= N0
e-ei/kT
Notons que si ei = 0, Ni = N0. Cette relation n’est valable que si tous les niveaux sont distincts et donc d’énergie différente. Si, au contraire, certains niveaux sont ki fois dégénérés (ont la même énergie), la formule précédente s’écrit :
Ni = ki N0 e-ei/kT
La loi de BOLTZMANN indique la fraction de molécules (particules) dans un état donné. Le nombre total de particules N est tel que :
2.31 N = N0 Si ki e-ei/kT
Ainsi N = S Ni, ce qui bien entendu va de soi et :
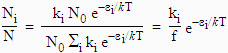
La grandeur f est simplement égal à Si ki e-ei/kT : c’est la fonction de partition (voir un cours de chimie théorique).
4. D'autres lois
En 1811, AVOGADRO a proposé son hypothèse :
Deux volumes égaux de gaz, s’ils sont à la même température et pression, contiennent le même nombre de molécules. En effet, la relation 2.15 permet d’écrire :
![]()
2.32
P =
2/3 Ec
N/V
Dans
cette relation Ec
est l’énergie cinétique des molécules.
Dans deux systèmes gazeux A et B tels que les pressions PA et
PB sont égales et où les volumes VA et VB
sont égaux, on peut écrire :
PA
= 2/3
EcA NA/VA
et PB
= 2/3
EcB NB/VB
Puisque la température
TA est identique à TB,
les énergies cinétiques sont aussi égales :
2.33
EcA =
EcB
Ce qui entraîne
que NA = NB.
4.2 La loi généralisée
des gaz parfaits
La relation 2.31 peut se réécrire sous la forme :
P
V =
2/3 Ec
N
En combinant cette équation avec la relation reliant l’énergie cinétique à la température pour chaque molécule (équation 2.17), en remplaçant le nombre N par le nombre de moles n, on obtient :
Ec
= 3/2 n R T
2.34
PV = n R T
C’est la loi généralisée des gaz parfaits.
Avant de parler de cette loi, il convient de faire une différence entre l’effusion et la diffusion. À l’aide de deux figures on comprendra la différence. La figure 2.8 montre le cas de l’effusion. Un gaz est enfermé dans une chambre sous une pression P. Les molécules de ce gaz peuvent traverser dans une autre chambre maintenue sous vide à travers un orifice dont le diamètre est un peu plus grand que le diamètre des molécules. Dans le compartiment sous pression, les molécules sont soumises à leur mouvement brownien et ce n’est que lorsque leur trajectoire les amènera directement dans l’orifice que ces molécules pourront traverser vers le volume vide. Sans entrer dans le détail, on montre que cette vitesse d’effusion est directement proportionnelle à la vitesse des molécules en phase gazeuse. Lorsque la température est la même pour deux gaz A et B, ce qui est le cas lorsqu’ils sont mélangés dans un même réacteur, on peut écrire (équation 2.32) :
EcA = EcB ou encore, 1/2 mA cA2 = 1/2 mB cB2
|
|
Figure 2.8. Effusion d’un gaz.
Ce qui entraîne
que :
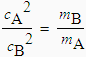
ou encore :
| 2.35 |
|
La vitesse
d’effusion d’un gaz à travers un orifice est inversement proportionnelle à
la racine carrée de sa masse moléculaire. Cette loi
est à la base du processus de séparation des isotopes 235U et 238U
sous la forme d’hexafluorure d’uranium pour l’enrichissement de
l’uranium pour les fins de son utilisation dans certains réacteurs nucléaires.
Le cas de la
diffusion est différent. La figure
2.9 montre deux récipients chacun contenant un gaz différent séparés par une
paroi poreuse. Les molécules du
gaz A du compartiment de gauche tendent à se déplacer vers le compartiment de
droite et inversement pour les molécules B du compartiment de droite.
La diffusion est contrôlée par les quantités de mouvement qui sont
transmises aux parois au moment de la diffusion.
À nouveau sans entrer dans le détail, on montre que la vitesse de
diffusion obéit à la même loi que celle de l’effusion.
Cela explique que les deux phénomènes sont très souvent confondus.
|
|
Figure 2.9. Diffusion d’un gaz.
5. Les mélanges de gaz idéaux
Qu’arrive-t-il lors du mélange de deux gaz idéaux ? Soient deux gaz A et B qui sont dans des volumes égaux V : l’un est à la pression PA, l’autre à la pression PB. Supposons que ces deux gaz sont mélangés et introduits dans un récipient lui aussi de volume V. La loi de DALTON dit que la pression du mélange est égale à somme des pressions PA et PB. On dit aussi que les pressions partielles des ces deux gaz sont respectivement PA et PB.
Ptotale = PA + PB.
Cette relation peut être généralisée à un nombre N de gaz :
2.36 Ptotale = PA + PB + … + Pi … + PN
De la même manière, la loi d’AMAGAT stipule que si N gaz à la même pression P occupent des volumes différents, s’ils sont mélangés et introduits dans un récipient lui aussi soumis à la même pression P, ils occuperont un volume égal à la somme de chacun des volumes individuels :
2.37 Vtotal = VA + VB + … + Vi … + VN
|
Les lois applicables aux gaz parfaits participent pleinement à la théorie atomique. La définition de la mole donnée au chapitre 1 prend également toute sa valeur. Les lois de BOYLE-MARIOTTE, de CHARLES, de GAY-LUSSAC, la théorie cinétique des gaz, y inclus la loi de GRAHAM sont des conséquences directes de la théorie atomique. De plus la vitesse des molécules gazeuses est intimement liée à la température absolue du gaz. En d’autres termes, le gaz absorbe de l’énergie principalement sous la forme d’énergie cinétique (déplacement des atomes ou des molécules qui le constituent). Il faut cependant ajouter que ces lois sont valides et largement observables dans la mesure où le gaz est dit idéal : les molécules sont dans des situations où elles n’interfèrent pas les unes avec les autres.
|
Liens utiles
sur le Web :
Le lecteur trouvera de nombreux sites sur le Web tant en français qu’en anglais. On en indique seulement quelques uns ici et ceux retenus ici ne découlent pas d’un quelconque classement basé sur des critères pédagogiques ou autres. Au lecteur de faire ses choix.
Dans le texte, les noms propres avec hyperliens réfèrent à des sites portant surtout sur la biographie du scientifique identifié.
On trouvera en plus quelques sites davantage orientés sur des éléments de concepts aux adresses suivantes.
- La distribution de vitesse de MAXWELL :
http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/kintem.html#c3
http://www.wikipedia.org/wiki/Maxwell-Boltzmann_distribution
- L’énergie cinétique moléculaire :
http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/molke.html
- Une animation sur la loi de CHARLES et GAY-LUSSAC :
http://www.grc.nasa.gov/WWW/K-12/airplane/aglussac.html
- Des animations en français
De nombreuses informations et des biographies sont accessibles dans le Dictionnaire interactif des sciences et techniques. Il faut s'inscrire et le site n'est pas gratuit. Cliquez sur http://www.sciences-en-ligne.com/comm/ et aussi ailleurs.
Problème N° 1
L’étude de l’oxygène à basse pression et à 0 °C a donné les résultats qui suivent :
| P (atm) | Volume (litre / g) |
| 1,000 | 0,699 81 |
| 0,750 | 0,933 28 |
| 0,500 | 1,400 27 |
| 0,250 | 2,801 20 |
P est la pression. Déterminez si, dans ces conditions, l’oxygène suit la loi de BOYLE – MARIOTTE.
Problème N° 2
Un baromètre fonctionnant mal (vide imparfait) indique une pression de 755 mm de mercure, la pression atmosphérique réelle est de 765 mmHg. La partie évacuée (soit disant vide) du tube barométrique est longue de 25 mm. Calculez la véritable pression atmosphérique lorsque la lecture du baromètre indique une pression de 745 mm.
Réponse
: P
= 752,14 mmHg
Problème N° 3
Par une méthode expérimentale appropriée on détermine que 1,3882 g de substance occupent un volume de 0,420 litre à 220 °C et cela sous une pression de 747 mmHg. Quel est le poids moléculaire de la substance ? Par ailleurs, l’analyse élémentaire de la substance révèle qu’elle contient 70,6 % de carbone, 5,88 % d’hydrogène et 23,52 % d’oxygène. Quelle est la formule moléculaire de la substance ?
Réponse : La formule molaire de la substance recherchée est : C8H8O2.
Problème N° 4
Des
gaz de combustion ont la composition suivante (pourcentage en volume) :
CO2 :
10,5 %; CO : 1,1 %; O2 : 7,7 % et N2 : 80,7
%.
En
supposant que les gaz agissent comme des gaz parfaits, calculez :
1-
le pourcentage en masse des composants ;
2-
le volume d’un kg de gaz sous une pression de 740 mmHg et à la
température de 80 °C
;
Réponse : d = 1,008 kg/ m3
Problème N°
5
Dernière mise à jour: 2021-07-02.
x x x x x x x x x x x x