|
|
|
Le chapitre précédent a montré comment les lois qui gouvernent le comportement des gaz idéaux s’insèrent bien dans le sillage de la théorie atomique. Les gaz ne sont cependant pas tous dans des situations idéales. Il va donc de soi d’étudier le comportement des gaz non idéaux, ou encore des gaz réels. Note : cette expression gaz réel est boiteuse puisqu’elle donne à penser que plusieurs gaz idéaux comme ceux observés à basse pression ou à haute température ne le sont pas ; ce qui est évidemment faux. Tout d’abord comment défini-t-on un gaz réel ou mieux non idéal ? Quelles sont les lois qui les gouvernent ?
|
1. Déviation d’un gaz réel
par
rapport au gaz idéal
On a vu dans le chapitre précédent le comportement théorique appréhendé d’un gaz idéal. On peut aborder le gaz réel d’au moins deux manières. Une première manière consiste à reprendre les éléments théoriques introduits dans ce chapitre 1 et à les modifier en tenant compte de la nature réelle des molécules. Cette entreprise bien que possible est hors des limites de ce premier cours relatif à la matière.
Une deuxième manière consiste à voir si les lois macroscopiques établies dans ce premier chapitre sont conservées ou si elles doivent être altérées, modifiées pour tenir compte de la réalité physique des molécules. C’est cette approche plus descriptive que déductive que nous retiendrons.
2. La déviation
par rapport à la loi de BOYLE-MARIOTTE
On a vu qu’à une température fixe, le produit pression ´ volume d’une quantité de gaz est constant. Ainsi, à température élevée, par exemple vers 200 °C, le produit PV devrait être indépendant de la pression. Cela est vrai tant et aussi longtemps que cette pression demeure relativement peu importante. Pour un gaz donné ce domaine de pression pourra s’étendre jusqu’à des pressions de 200 bar (» 200 atmosphères). Ce n’est cependant plus vrai lorsque la pression P dépasse cette valeur. Le produit P V tend à croître au fur et à mesure que la pression croît (Fig. 3.1). On se rappellera que sur cette figure, la loi de BOYLE-MARIOTTE est représentée par les lignes pointillées.
|
|
Figure 3.1. Variation du produit PV en fonction de la pression dans le cas d’un gaz réel.
Si le précédent échantillon est refroidit au voisinage de la température du laboratoire, 20 °C par exemple, la déviation du produit PV tant à augmenter. Ce produit diminue quelque peu jusque vers 200 bar, puis s’accroît rapidement au-dessus de cette pression. À une température plus basse les variations du produit PV sont maintenant beaucoup plus importantes et le comportement de ce produit s’éloigne définitivement de la constance prévue par la loi de BOYLE-MARIOTTE (Fig. 3.1).
En généralisant quelque peu, on dira que la déviation par rapport à la loi de MARIOTTE croît soit avec l’augmentation de la pression, soit avec la diminution de la température.
En changeant le gaz sous expérimentation, on observe que ces écarts à l’idéalité dépendent de la nature du gaz. On verra plus tard, même si on peut déjà le soupçonner, que plus la molécule gazeuse est complexe et plus ces écarts sont importants (Fig. 3.2).
|
|
Figure 3.2. Variation du produit PV en fonction de la pression dans le cas de l’hydrogène et de l’azote.
2.1. L’effet
de covolume
Afin d’expliquer les écarts précédemment observés, on peut raisonnablement proposer une première correction à la loi de BOYLE-MARIOTTE. En effet, si V est le volume du réacteur dans lequel est confiné l’échantillon, le volume réellement disponible dans lequel se meuvent les molécules doit être corrigé pour l’espace occupé par les molécules elles-mêmes. Le volume disponible devient égale à V – b, b étant le volume réel des molécules, ce que l’on nomme aussi le covolume. Le produit PV devient donc :
P (V – b) = n R T
n est le nombre de moles contenues dans l’échantillon gazeux, R est la constante des gaz parfaits et T la température en kelvin. Si la quantité de gaz est justement celle d’une mole, on écrit :
![]()
2.2. Les interactions intermoléculaires
Une deuxième correction peut facilement être apportée. En effet, les molécules réelles ne sont pas sans interférer les unes avec les autres. Cela est d’autant plus évident que ces molécules portent des moments dipolaires. Sans porter de charges électriques, elles sont alors formées de régions plus fortement chargées positivement et d’autres plus fortement chargées négativement. Ces régions vont s’attirer ou au contraire se repousser mutuellement. Sans entrer dans le détail, si r est la distance entre les molécule, l’énergie potentielle attractive Eattr est de la forme :
Eattr = - b / r6
L’énergie répulsive Erép est de la forme :
Erép = a / r12
L’énergie potentielle d’interaction Einteraction est donc :
3.1 Einteraction = a / r12 - b / r6
Ce potentiel est appelé potentiel de LENNARD-JONES. La figure 3.3 montre le cas de l’interaction entre les atomes d’hélium en phase gazeuse. La courbe relative à l’interaction entre deux atomes d’hélium dans leur état fondamental ne montre pas de minimum. Seul le potentiel répulsif a une constante a finie : b est voisin de zéro. Ce potentiel de répulsion devient vite négligeable avec l’augmentation de la distance r. Dans le cas d’une paire d’atome d’hélium, dont l’un est dans le premier état électronique excité, il existe un potentiel attractif non nul, de telle sorte que b (He*-He) est différent de zéro.
|
|
Figure 3.3. Forme des courbes de potentiel de LENNARD-JONES dans le cas de deux atomes d’hélium.
Dans le cas général, les courbes de potentiel attractives et répulsives sont bien caractéristiques. L’énergie du système est égale à la somme des deux énergies potentielles. Il existe une distance r0 où elles sont égales, déterminant ainsi une position d’équilibre entre les atomes ou les molécules (Fig. 3.4). Cela n’implique pas que les atomes ou les molécules vont ainsi demeurer à une distance fixe les uns des autres. Sous l’effet de l’énergie thermique disponible (essentiellement sous forme d’énergie cinétique), les atomes et molécules vont se mouvoir les uns par rapport aux autres.
|
|
Figure 3.4. Forme générale des courbes de potentiel de LENNARD-JONES dans le cas de deux molécules.
Pour tenir compte de ces interactions entre les molécules gazeuses, VAN DER WAALS a introduit une correction au terme P de l’équation de BOYLE-MARIOTTE sous la forme
P + a / V2
Le terme en V2 qui se trouve au dénominateur permet de traduire que, pour une quantité fixe de gaz, plus le volume est grand et plus les molécules sont éloignées les unes des autres. Il en résulte que cette correction est d’autant plus faible que le volume est grand.
En résumé, les deux précédentes corrections transforment la loi de BOYLE-MARIOTTE sous la forme de la loi de VAN DER WAALS :
3.2
(P + a /V2) (V -
b) =
n R T
Pour une mole, la loi devient :
| 3.2' |
|
= R T |
|
|
Une première conséquence, si le volume V devient très grand, les termes correctifs apportés à la pression P et au volume V deviennent négligeables : le facteur (V – b) tend vers la valeur de V et le rapport a/V2 tend vers zéro. On retrouve la loi de BOYLE-MARIOTTE : cette loi constitue la loi limite de la loi de VAN DER WAALS lorsque le volume devient très grand, voire infini.
Les
paramètres a et b sont des caractéristiques de chacun des gaz.
Le tableau 3.1. donne quelques valeurs de ces paramètres.
Tableau 3.1. Valeurs des paramètres de l’équation de VAN DER WAALS
| Gaz |
a (bar litre2 mol-2) | b (litre mol-1) | Gaz | a (bar litre2 mol-2) | b (litre mol-1) |
| He | 0,034 | 0,0237 | NH3 | 4,17 | 0,0305 |
| Ar | 1,35 | 0,0322 | H2O | 5,46 | 0,0318 |
| Ne | 0,211 | 0,0171 | CO2 | 3,59 | 0,0427 |
| H2 | 0,244 | 0,0266 | CH4 | 2,25 | 0,0428 |
| O2 | 1,36 | 0,0318 | SO2 | 6,71 | 0,0564 |
| N2 | 1,39 | 0,0391 | C2H4 | 4,47 | 0,0571 |
| CO | 1,49 | 0,0399 | C2H6 | 5,49 | 0,0638 |
| HCl | 3,67 | 0,0408 | CHCl3 | 15,17 | 0,1022 |
| HBr | 4,45 | 0,0443 | CCl4 | 20,39 | 0,1383 |
| Unités : 1 bar litre2 mol-2 = 0,101 N m4 mol-2 | |||||
L’équation d’état de VAN DER WAALS rend mieux compte que celle de BOYLE-MARIOTTE de la pression d’un gaz à basse température et à pression relativement élevée. Elle n’est cependant pas parfaite. D’autres équations d’état se proposent d’améliorer cette réalité (voir plus bas).
Le tableau 3.2 montre la comparaison entre les lois de BOYLE-MARIOTTE et de VAN DER WAALS dans deux cas particuliers.
Tableau
3.2. Comparaison entre les lois de
BOYLE-MARIOTTE et de VAN DER WAALS
(T = - 100 °C)
| Pression
observée (bar*) |
Pression idéale : loi de MARIOTTE | Pression de VAN DER WAALS |
|
hydrogène |
||
| 50 | 48,7 | 50,2 |
| 75 | 72,3 | 75,7 |
| 100 | 95,0 | 100,8 |
|
gaz carbonique |
||
| 50 | 57,0 |
49,5 |
| 75 | 92,3 |
73,3 |
| 100 | 133,5 |
95,8 |
| *
: 1 bar = 105 Pa s =
101 080 Nm-2
»
1 atm. |
||
3.1.
L’équation de VAN DER WAALS
Soit donc cette relation :
(P + a/V2) (V - b) = n R T
Cette relation se traduit sur un plan analytique P,V selon ce qui apparaît sur la figure 3.5. La courbe P = f(V) se décompose en trois parties selon que V < 0, 0 £ V £ b, ou que V > b. Bien évidemment, le volume des molécules ne peut pas être négatif (région A de la figure 3.5). La condition pour laquelle le volume V est compris entre 0 et la valeur b est tout autant physiquement inacceptable (région B de la figure 3.5) puisque les molécules occupent le volume b. Seule la partie C du graphe présente donc un intérêt physique et sera donc étudiée.
|
|
Figure 3.5. Tracé de la courbe de VAN DER WAALS dans le plan pression – volume.
Soit donc la condition V > b. Voyons comment se comporte la fonction P = f(V) lorsque la température T varie. On remarque que si la température est très grande la courbe ressemble à une portion d’hyperbole. En fait, comme on l’a dit plus haut, la courbe de VAN DER WAALS rejoint celle de BOYLE-MARIOTTE (région C de la figure 3.5).
Au fur et à mesure que la température décroît, cette portion d’hyperbole se déforme peu à peu (Fig. 3.6). Il apparaît progressivement une sorte de bosse qui fait place à un point d’inflexion horizontal à la température T = Tc. À température plus basse il se forme une déformation en forme de S qui devient de plus en plus importante avec un abaissement de plus en plus important de la température.
|
|
Figure 3.6. Courbe de liquéfaction dans le plan pression – température.
3.2. Les coordonnées du point critique
Les coordonnées du point d’inflexion correspondent aux coordonnées du point critique : Pc, Vc et Tc. On remarque que quelles que soient les conditions expérimentales, pourvu que la température soit supérieure à la valeur de la température critique Tc, il est impossible de liquéfier le gaz. Par contre si T < Tc, on observe la liquéfaction.
Pour obtenir les coordonnées du point triple, le point d’inflexion observé à la température Tc, il suffit d’écrire qu’en ce point, non seulement la dérivée première, mais également la dérivée seconde de la fonction P = f(V), sont égales à zéro. Faisons ces calculs sur l’équation d’état correspondant à une mole.
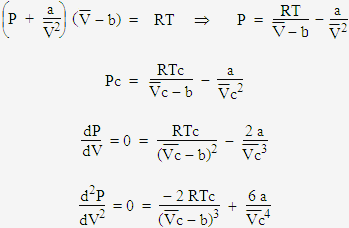
On
a trois équations à trois inconnues. Ce
système permet donc d’obtenir les valeurs des coordonnées du point critique
en fonction des paramètres a et b. On
obtient ainsi :
| 3.3a |
|
3.3b
Þ
a = (27/8)
R Tc b = 27 Pc b2
R
Tc / 8 =
Pc b =
Pc Vc / 3
3.4
Pc Vc =
3/8 R Tc
On
voit ainsi, qu’au point critique, la loi de BOYLE-MARIOTTE est quelque peu
modifiée.
Tableau 3.3. Valeurs critiques pour quelques gaz
|
Gaz |
Tc (K) |
Pc (bar) |
Vc |
Gaz |
Tc
(K) |
Pc (bar) |
Vc |
|
He |
5,2 |
2,2740 |
57,47 |
NH3 |
405,4 |
113 |
|
|
Ar |
150,86 |
48,979 |
74 |
H2O |
647
±
2 |
220,64 |
55,95 |
|
Kr |
209,46 |
55,20 |
91,28 |
CO2 |
304,18 |
73,80 |
94,34 |
|
H2 |
33,3 |
12,8 |
|
CH4 |
190,6 |
46,1
±
0,3 |
99,0 |
|
O2 |
154,58 |
50,43 |
73,52 |
C2H2 |
308,3
±
0,1 |
61,38
±
0,1 |
112,2 |
|
N2 |
126,19 |
33,978 |
89,47 |
C2H4 |
282,5
±
0,5 |
50,6
±
0,5 |
131,1 |
|
CO |
134,45 |
34,9875 |
90,06 |
C2H6 |
305,3
±
0,3 |
49
±
1 |
147 |
|
HCl |
324,68 |
82,56 |
|
CHCl3 |
537
±
2 |
53,287 |
243 |
|
Cl2 |
416,96 |
79,91 |
122,93 |
CCl4 |
556,36 |
44,93 |
276 |
|
SO2 |
430,4 |
|
|
benzène |
562,0
± 0,8 |
48,9
± 0,4 |
250
± 30 |
3.3.
Propriétés du point critique
On a déjà mentionné qu’au delà de sa température critique on ne peut plus liquéfier le gaz. Sur le diagramme pression – température la courbe de liquéfaction délimitant la région des phases gazeuse et liquide se termine abruptement à la température critique (Fig. 3.8).
Cette brutale coupure dans la courbe de liquéfaction doit se retrouver dans les propriétés comparées des deux phases. Par exemple, si l’on examine la densité des deux phases, à pression constante, on se rend compte que la densité du liquide et la densité du gaz se rapprochent l’une de l’autre lorsque la température du système se rapproche de la température critique. À cette température, les deux densités sont égales. Ainsi, les propriétés physiques des deux phases se confondent à la température critique de telle sorte que l’observateur extérieur ne peut plus différencier une phase de l’autre (Fig. 3.7).
|
|
Figure 3.7. Expérience du point critique.
Imaginons en effet un observateur situé sur le plan Pression – Température au voisinage du point critique d’un gaz. Supposons qu’il est situé sur l’un des sommets du quadrilatère ABCD, plus précisément au point A. Il est donc situé au sein de la phase gazeuse. Imaginons que l’on augmente la pression, ou mieux, que l’observateur se déplace sur le côté AB (en direction de B) de ce quadrilatère. Il traverse la courbe de liquéfaction et se trouve donc maintenant dans la phase liquide. Il a pu observer une variation importante des propriétés physiques du milieu lors de son passage de la phase gazeuse à celle liquide.
En ce point B augmentons la température sans changer la pression, l’observateur se déplace vers le point C. En C, diminuons la pression sans changement de température : l’observateur parvient au point D. Diminuons maintenant la température sans modifier la pression. L’observateur se déplace vers et parvient au point A. Hors, depuis son séjour au point B, alors qu’il était en phase liquide, l’observateur n’a observé aucun changement de phase. Il est donc amené à penser qu’il se trouve encore en phase liquide, alors qu’il se trouve bien dans la phase gazeuse. Que s’est-il passé ?
En réalité on montre qu’en approchant de la température critique, les propriétés physique du liquide et celle du gaz convergent vers des valeurs identiques : le gaz et le liquide se confondent au point critique. La figure 3.8 illustre les valeurs comparées de la densité des phases liquide et gazeuse de l’anhydride sulfureux au voisinage de son point critique.
|
|
Figure 3.8. Variation de la densité des deux phases liquide et gazeuse au voisinage du point critique : cas du SO2.
3.4.
Isotherme réduit
L’équation
de VAN DER WAALS change donc avec chaque gaz.
Il existe une forme réduite de cette équation valide pour n’importe
quelle substance gazeuse. En remplaçant
les constantes a et b par les valeurs obtenues en fonction des conditions
critiques, l’équation de VAN DER WAALS devient :

Divisons chaque membre de cette équation par Pc et Vc (en fait la première parenthèse par Pc et la seconde par Vc), il vient :
|
|
|
En
utilisant la relation 3.4, on obtient :
![]()
Posons
en effet P
= P/Pc,
J
= V/Vc
et
Q
= T/Tc; P, J
et Q
sont appelées les variables réduites.
L’équation précédente devient :
| 3.6 |
|
L’équation
réduite est la même pour tous les gaz. Deux
fluides sont dits dans des états correspondants si leurs variables réduites
sont les mêmes.
En
1881, VAN DER WAALS avait remarqué la relation 3.6 constituait une relation
convenable pour n’importe quel gaz dans des conditions modérées de pression.
Si cette suggestion est réelle, alors le produit ( Pc Vc / n R Tc )
devrait être le même pour tous les gaz. Les données incluses dans le tableau
3.3 permettent de vérifier la suggestion en calculant le produit Pc Vc / Tc = 23,48
(s = 0,85). Ce
calcul ne tient pas compte de la valeur obtenue pour l’eau : Pc Vc / Tc
(eau) = 19,08. Les valeurs
individuelles s’étalent entre 21,75 pour le benzène et 25,13 pour l’hydrogène.
Une
manière intéressante est d’introduire le facteur de compression z tel que :
P V
= z n R T
Les
ingénieurs chimistes qui travaillent souvent avec des gaz sous pression ont préparé
des graphes qui montrent la variation de z avec P et T.
Ils ont ainsi montré que, même à hautes pressions, z est une
fonction universelle des variables réduites P et Q.
La figure 3.9 illustre la
valeur de la fonction z pour différentes valeur de Q.
Les valeurs réelles obtenues pour plusieurs gaz se trouvent à moins de
1 % des courbes.
|
|
Figure
3.9. Facteur de compression z en
fonction des variables réduite P
et Q.
4.
Relations P – V – T entre les phases liquide et gazeuse
4.1. Les phases liquide et gazeuse
Revenons
sur les courbes de VAN DER WAALS, et plus spécifiquement lorsque la température
du gaz est inférieure à la température critique. Supposons que l’échantillon, du gaz carbonique par
exemple, est sous une pression de
plus de 80 atmosphères à la température de 20 °C. Il
est donc gazeux. Si la pression
diminue, le gaz prend de l’expansion : il augmente de volume. L’échantillon parcourt le segment curviligne du point a
vers le point b (Fig. 3.10). En
b, l’échantillon entre dans la région en forme de S
couché de la courbe de VAN DER WAALS.
Au lieu de suivre le segment curviligne bcd, il suit le segment
rectiligne bd : l’échantillon est entièrement liquide : le
volume augmente et la pression demeure constante (»
64 atm). Parvenu en d, une
diminution subséquente de la pression, entraîne la vaporisation de l’échantillon
et une augmentation de volume. L’échantillon
progresse vers le point e.
|
|
Figure 3.10. Courbe de liquéfaction dans le plan pression – température du gaz carbonique.
Note
complémentaire : on montre que les deux triangles curvilignes situés de
part et d’autre du segment bd ont des surfaces égales.
On vient de voir que pour un gaz, il existe un lien une relation entre la pression, la température et le volume. Si la pression et la température sont choisis comme variable, alors :
![]()
Dans le cas du gaz idéal,
P V = n R T
4.2. Les coefficients de dilatation thermique
4.2.1. Cas des transformations isobares
Si la pression P est fixée, est constante, cette dernière relation montre que si la température croît le volume croît. On définit le coefficient de dilatation thermique à pression constante a de la manière suivante : c’est l’augmentation ¶V de volume pour une augmentation ¶T de la température relativement à un volume V sans changement de la pression.
| 3.7 |
|
L’unité de a est l’inverse d’une température : [a] = [T]-1.
Déjà en 1847, REGNAULT avait observé la dilatation thermique des gaz et avait mesuré une augmentation de volume de 1/273 pour une augmentation de 1 °C. Le volume V d’un gaz à une température quelconque q °C et son V0, à une température de référence à 0 °C, sont reliés par la relation :
V = V0 (1 + a0 q) avec a0 = 1/273
Considérons l’équation d’état de MARIOTTE :
P V = n R T ou encore V = n R T / P
Le volume V est donc proportionnel à la température T : V = a T. Pour deux températures T1 et T2, on obtient :
V1 = a T1 et V2 = a T2
V1 - V2 = a (T1 - T2)
En utilisant les grandeurs molaires la même relation devient :
|
|
= (R/P) (T1 - T2) |
Pour une différence de 1 °C,
|
|
= (R / P) |
Sous
la pression d'une atmosphère, P =
101 325 Pa ou encore 101 325 N /
m2. Le volume
d’une mole à 0 °C est de 22,4 litres.
Remplaçons R et P de cette dernière relation par leur valeur en SI, on obtient :
|
|
= 8,314
41 J/(mol · K) /101 325 P
= 8,314 41 N · m /(mol · K) /101 325 N / m2 = 8,205 68 10-5 m3 /(mol · K) |
Ramenons
le volume à celui d’une mole dans les conditions normales :
|
|
|
|
|
= 1/273 K-1 |
La valeur maintenant admise est :
3.8 1/a = 273,15 ± 0,02 K
4.2.2. Cas des transformations isothermes
Si au contraire c’est la température qui est fixée, on définit un coefficient de dilatation volumique b à température constante tel que : c’est l’augmentation ¶V de volume pour une augmentation ¶P de la pression relativement à un volume V sans changement de température.
| 3.9 |
|
On conçoit que l’augmentation de pression a l’effet de diminuer le volume : cela justifie l’introduction du signe négatif dans l’équation 3.9. L’unité de b est l’inverse d’une pression : [a] = [P]-1.
4.3. Relations entre a et b
Puisque la fonction V dépend de la température et de la pression, V = f(T, P), on peut écrire :
![]()
D’où en remplaçant par les définitions précédentes des coefficients de dilatation à pression et à volume constants :
| 3.10 |
dV = a V dT - b V dP |
En réarrangeant cette équation 3.10 avec la précédente, on obtient :
![]()
Considérons la fonction P
= f(V, T), on peut écrire
aussi :
![]()
| Donc |
 |
| et 3.11 |
Dans un système fermé la variation de pression engendrée par une variation de température à volume constant est donnée par la relation 3.11.
Autre relation
| Considérons le produit |
| On peut écrire : (Voir 3.7 et 3.11) |
 |
| Comme |
|
on peut écrire les dérivées partielles suivantes : |
| Cela entraîne que |  |
On montrera que pour un gaz parfait ou idéal, la différence (voir chapitre 1 du Cours de thermodynamique)
![]()
| Par conséquent, pour un gaz idéal : |
5.1. Le viriel
On peut donc soupçonner que la loi de VAN DER WAALS est parfois trop simple pour bien traduire le comportement des gaz en particulier lorsqu’ils sont fortement comprimés et à basse température. Cette loi peut se mettre sous la forme d’un développement en série dont on reconnaîtra aisément la loi de MARIOTTE dans le premier terme et la correction de VAN DER WAALS dans le second.
| 3.12 |
|
Les coefficients A, B, C, D, … sont connus sous le nom du 1er, du 2nd, du 3e , … coefficient du viriel. Ces coefficients sont de plus en plus petits au fur et à mesure que l’on passe de A, à B, puis à C, … Par exemple, pour l’argon, le second coefficient se fait sentir à des pressions supérieures à 100 bar. Le tableau 3.4 donne quelques valeurs du premier coefficient du viriel pour deux gaz.
Tableau 3.4. Quelques valeurs du 1er coefficient du viriel
| T (°C) | Volume
molaire (litre / mole) |
Azote A (litre/mole) |
Oxyde
de carbone |
| - 50 |
18,312 |
- 2,879 | - 3,688 |
| 0 | 22,414 |
- 1,051 | - 1,482 |
| 100 | 30,619 |
0,666 |
0,404 |
| 200 | 38,324 | 1,476 | 1,316 |
On
trouvera d’autres valeurs des
coefficients A, B, C,… dans la
littérature. Par exemple :
-
Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, 4e
édition, The MacMillan Company, New York (1965);
-
Moore, W. J., Basic Physical Chemistry, Prentice-Hall, inc., Englewood
Cliffs, New Jersey (1982).
Il est intéressant de constater que le premier coefficient du viriel est tantôt négatif et tantôt positif. Il existe donc une température pour laquelle il devient nul. Cette température est appelée la température de BOYLE. À cette température, la loi de MARIOTTE (ou de BOYLE-MARIOTTE pour les anglophones), est valide sur un large domaine de pression.
La température de BOYLE peut être déterminée à partir de l’équation de VAN DER WAALS. En effet, l’équation 3.2 peut-être réécrite sous la forme (équation 3.2') :
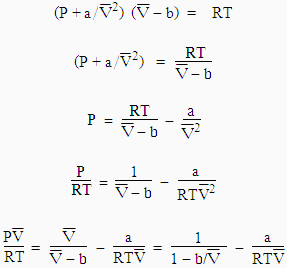
En
reconnaissant que le covolume b est beaucoup plus petit que le volume molaire,
tout au moins dans des limites de pressions raisonnables, le premier terme du
dernier membre de cette équation peut être développé en série.
Posons

puisque
x
<< 1 car b <<
![]()
Remplaçons la fraction par son développement en série dans l’équation d’état. On obtient :

Le premier coefficient de cette équation est évidemment nul lorsque :
a = b R T
En remplaçant les valeurs a et de b par les valeurs critiques obtenues plus haut, on obtient la température de BOYLE TB :
a
= b R TB
=
(27/8) R Tc b
3.13 TB = (27/8) Tc
Il existe d’autres équations d’état comme, par exemple, celle de KAMERLINGH ONNES (1901) :
| 3.14 |
|
= A + B P
+ C P2
+ D P3
+ … |
5.2. L’équation d’état de BEATTIE-BRIDGEMAN
Elle est de la forme :
| 3.15 |
|
![]()
Les coefficients b, g et d ont les valeurs suivantes :
b = R T B0 - A0 + R c / T2
g = - R T B0 b + A0 a - R c B0 / T2
d = R B0 b c / T2
Tandis que A0, B0, a, b et c sont des constantes caractéristiques pour chaque gaz.
Tableau
3.5. Coefficients de l’équation
d’état de BEATTIE-BRIDGEMAN
pour quelques gaz
| Gaz | A0 | a | B0 | b | c |
| He | 0,0216 | 0,059
84 |
0,014 00 | 0 | 0,004
104 |
| Ne | 0,2125 |
0,2196 |
0,020 60 | 0 | 0,101
104 |
| Ar | 1,2907 |
0,023
28 |
0,039 31 | 0 | 5,99
104 |
| H2 |
0,1975 |
-0,005 06 |
0,020
96 |
-0,043 59 |
0,050
104 |
| N2 |
1,3445 | 0,02617 |
0,050 46 | -0,006 91 | 4,20
104 |
| O2 |
1,4911 | 0,025
62 |
0,046
24 |
0,004
208 |
4,80
104 |
| CO2 |
5,0065 |
0,071
32 |
0,104 76 | 0,072
35 |
66,0
104 |
| CH4 |
2,2769 |
0,01855 | 0,055 87 | -0,015 87 | 12,83
104 |
| Note
: P = 1 bar; volume (litre/mole). |
|||||
5.3. Une autre équation
On connaît aussi l’équation d’état de BERTHELOT. Celle-ci s’obtient en dérivant la relation d’état de VAN DER WAALS par rapport au volume :
|
|
|
On introduit les conditions critiques pour le gaz considéré : Pc, Vc, et Tc. On a déjà vu la signification exacte de ces valeurs critiques. On montre en effet que, dans le plan P = f(V), les coordonnées du point critique peuvent être déterminées à partir des dérivées première et seconde :
| 3.17 |
|
L’équation 3.6 et les deux équations 3.7 permettent d’obtenir les coordonnées Pc, Vc et Tc sous la forme Pc = f1(A,B), Vc = f2(A,B) et Tc = f3(A,B), ou encore A = f1'(Pc, Vc, Tc) et B = f2'(Pc, Vc, Tc). Finalement, on obtient la relation suivante :
| 3.18 |
|
En utilisant les grandeurs molaires,
![]()
5.4. Également l’équation d’état de DIETERICI
Cette dernière est de la forme :
| 3.19 |
|
|
Le gaz non idéal résulte des interactions intermoléculaires tel que cela peut être observé à basse température et à haute pression au moins pour plusieurs gaz. En introduisant des paramètres convenables pour tenir compte de ces interactions, les lois qui gouvernent les comportements de ces gaz sont un peu plus complexes que celles observés dans le cas des gaz parfaits. Par exemple, la loi de VAN DER WAALS est évidemment plus complexe.
|
Le Handbook of Chemistry and Physics, CRC Press, contient une grande variété et quantité d’informations très utile au chimiste. Ainsi, on trouve dans la 70e édition, 1989-1990, les tables suivantes :
| Nom
de la table |
Description
sommaire |
pages |
| Coefficients
de VAN DER WAALS |
Valeurs pour une centaine de gaz | D-190 |
Liens intéressants :
On trouvera une animation simple de la loi de BOYLE-MARIOTTE à l’adresse suivante :
http://www.grc.nasa.gov/WWW/K-12/airplane/aboyle.html (visité le 2019-02-12).
Problème Nº 1
La loi de VAN DER WAALS indique que le volume physique (le covolume) d’une mole d’éthane est de 0,0638 litre/mol. À partir de cette valeur, calculez :
a- le diamètre moyen des molécules et le libre parcours moyen (conditions TPN);
b- la vitesse moyenne et la vitesse quadratique moyenne des molécules (conditions TPN);
c- le nombre de collisions par seconde.
Réponse
: Z
= 1,95 1010
collisions par seconde
Les coefficients a et b de l’équation de VAN DER WAALS pour l’éthane, C2H6, sont respectivement 5,41 l2·atm·mol-2 et de 0,064 06 l·mol-1. Calculez le diamètre moyen des molécules d’éthane.
Réponse
: r
= 0,134 nm
Problème
Nº 4
Un échantillon de gaz carbonique contient n molécules à une pression de 120 atm et une température de 70 ºC. Calculez en fonction de n le produit P V dans le système litre-atmosphère, en calories et dans le système international
a- par la formule de BOYLE-MARIOTTE et
b- par la formule de BERTHELOT
Problème Nº 5
La densité de l’éthanol gazeux est donnée en fonction de la température. Déterminez graphiquement la température critique de l’éthanol. Essayez d’en déduire la densité critique de ce composé.
| T (°C) | 100 | 150 | 200 | 220 | 240 |
| rliq | 0,716 | 0,649 | 0,557 | 0,496 | 0,382 |
| rvap | 0,0035 | 0,019 | 0,051 | 0,085 | 0,172 |
Réponses : TC = 246 ± 1 °C et rC = 0,27 ± 0,01.
Problème Nº 6
Sachant que la pression critique et la température critique du butane normal sont respectivement 37,5 atm et 152 °C, calculez les constantes de VAN DER WAALS de ce gaz.
Réponse : a = 15,31 litre2 atm mol-2.
On donne les constantes critiques du monoxyde de carbone, CO :
Tc
= 134,4 K, Pc 35,1 atm et Vc = 90,0 cm3 mol-1
a- Calculez les constantes de l’équation de VAN DER WAALS dans le système litre-atmosphère et en SI.
b- En déduire le diamètre moyen des molécules d’oxyde de carbone.
a- Les coefficients de l’équation de KAMERLINGH ONNES pour le monoxyde de carbone sont à 0 °C (la pression P est exprimée en atmosphère et les volumes le sont en litre mol-1) :
A = 22,414 ; B = - 1,4825 10-2 ; C = 9,823 10-5 ; D = 7,721 10-8 et E = 1,947 10-11
Calculez la densité de CO à 0 °C et sous une pression de 100 atm.
b- Calculez la même densité en utilisant la loi de MARIOTTE dans les mêmes conditions expérimentales.
Réponse : d = 124,97 g/litre
Faire le même calcul en utilisant l’équation de VAN DER WAALS. Les valeurs des coefficients de cette équation ont été calculés dans le problème précédent.
Dernière mise à jour : 2019-02-12.
x x x x x x x x x x x x