|
|
CHAPITRE VII
DIFFUSION DE LA LUMIÈRE - EFFET RAMAN
|
La diffusion de la lumière par une molécule
diatomique obéit aussi à des lois bien précises. On distingue plusieurs processus de
diffusion. Parmi ceux-ci, on retrouve l’effet RAMAN qui met en cause des transitions entre divers
niveaux d’énergie de rotation et de vibration. Quelles sont les lois
qui décrivent l’effet RAMAN ? Quel est
l’intérêt de cet effet pour la connaissance des molécules ? |
L’effet RAMAN résulte d’un processus de diffusion de la lumière par les molécules. Nous commencerons donc par étudier le phénomène de diffusion normale avant de passer à l’effet RAMAN. Notons dès maintenant que le processus de diffusion de la lumière par des molécules se distingue aussi des phénomènes étudiés en spectroscopie micro-onde (Chapitre 3)et en spectroscopie infrarouge (Chapitre 4). Dans ces derniers phénomènes, il y avait soit absorption, soit émission de lumière, à l’échelle de la molécule on dira qu’il y avait soit absorption, soit émission de photon. Dans le cas de la diffusion, comme le laisse supposer le mot, la lumière est déviée de sa trajectoire au moment où elle passe dans le champ moléculaire. Sans entrer davantage dans les détails de ce mécanisme d’interaction molécule-photon, la diffusion est le résultat d’une interaction de nature différente de celle observée et étudiée en spectroscopie : voir les modules relatifs à la rotation, à la vibration et à la rotation-vibration.
7.2 Diffusion de la lumière
Nous étudierons d’abord la diffusion de la lumière par un milieu trouble (un milieu transparent contenant des particules) ce que l’on nomme l’effet Tyndall. Nous verrons ensuite, le même phénomène lorsque ces particules sont des molécules et nous considérerons la propriété de polarisation de la lumière.
a. Diffusion par un milieu trouble - effet TYNDALL
Le dispositif de l’observation expérimentale de la diffusion est simple (Fig. 7.1). Un faisceau de lumière incidente est introduit dans une cellule contenant l’échantillon à étudier. Un système de fentes permet de recueillir un mince faisceau qui est ensuite envoyé à travers un système dispersif. Ce système est constitué d’un prisme ou mieux d’un réseau. Un système d’analyse de la lumière diffusée complète l’appareillage. Ce peut être un écran convenable, un système d’enregistrement photographique, ou un équipement électronique plus élaboré permettant une analyse beaucoup plus fine des observations avec un enregistrement de l’intensité diffusée en relation avec la longueur d’onde.
|
|
Figure 7.1. Dispositif schématique pour l’observation de la diffusion de la lumière.
L’observation ultramicroscopique de fines particules (quelques nanomètres) est permise parce que chaque particule diffracte dans toutes les directions une partie de la lumière qui provient de l’éclairage latéral. Si le nombre de particules augmente, l’observation individuelle des particules n’est plus possible, mais en même temps la quantité de lumière diffractée augmente; on dit alors que le milieu diffuse la lumière.
Cette diffusion, appelée effet TYNDALL, a été découverte par John TYNDALL, en 1859, mais surtout étudiée par Lord RAYLEIGH qui a proposé une loi reliant l’intensité I de la lumière diffusée et la longueur d’onde l de la lumière incidente :
| (7.1) |
I = k / l 4 |
Autrement dit, les courtes longueurs d’onde sont diffusées de façon beaucoup plus intenses que les grandes comme on peut l'observer, par exemple, sur un précipité fin de chlorure d’argent. Cette loi n’est valable que si la dimension des particules est petite par rapport à la longueur d’onde. Si la dimension des particules devient plus grande que la longueur d'onde, la réflexion normale devient le phénomène prépondérant et la loi de RAYLEIGH ne s’applique plus. La lumière émanant du milieu est alors de couleur blanche.
b. Diffusion moléculaire
Les molécules étant de petites particules, elles diffusent la lumière. Le bleu du ciel est un exemple d’observation facile. Comme le ciel est d’autant plus bleu qu’il est pur, on est bien obligé d’admettre que ce sont réellement les molécules d’air qui diffusent la lumière. Les liquides diffusent également avec une intensité beaucoup plus grande que l’air, par suite du plus grand nombre de molécules par unité de volume.
Des relations mathématiques lient également l’intensité de lumière diffusée, à la masse moléculaire des particules. Ces relations sont à la base de la mesure des masses moléculaires des macromolécules.
Par ailleurs, d’autres propriétés de la lumière sont modifiées lors des phénomènes de diffusion de la lumière. Il convient de rappeler certaines propriétés associées à un faisceau lumineux. En général, une lampe quelconque produit un faisceau de lumière couvrant une région du spectre électromagnétique : le visible, par exemple. On qualifie ce faisceau de lumière blanche. À l’aide d’un système dispersif comme celui rapidement esquissé dans la figure 1, on peut sélectionner une longueur d’onde et rendre le faisceau monochromatique. À ce faisceau de lumière monochromatique est associé un vecteur vibrant de manière aléatoire dans diverses directions perpendiculaires à la direction de propagation du faisceau.
On peut polariser ce faisceau en intercalant sur son parcours un cristal polarisant qui ne laisse passer que les vecteurs vibrant dans une seule direction (Fig. 7.2). Ce cristal, prisme de Nicol, jadis un spath d’Islande et aussi appelé un Nicol polariseur, est convenablement taillé pour permettre cette polarisation. La lumière qui sort de ce cristal est dite polarisée : le vecteur vibrant est orienté dans une seule direction.
Pour observer cette polarisation, on ajoute sur le parcours du faisceau un second Nicol dit analyseur. Ce cristal est tout à fait identique au précédent sauf qu’il est installé sur une bague qui permet de le faire tourner autour de l’axe de propagation de la lumière. Lorsque le plan de polarisation de ce second Nicol est parallèle à celui du Nicol polariseur, le vecteur vibrant du faisceau lumineux passe à travers ce second cristal.
|
|
Figure 7.2. Formation et observation de la lumière polarisée.
Si, par contre, on le fait tourner pour amener son plan de polarisation à 90° du premier Nicol, le vecteur vibrant n'a plus la possibilité de traverser ce second Nicol. On observe alors une extinction de lumière. En poursuivant la rotation de ce Nicol jusqu'à 180° l'observateur retrouvera l'intensité lumineuse.
Si maintenant en on fait tourner ce second Nicol (C dans la figure 7.3) pour amener son plan de polarisation à un angle a par rapport au premier (B sur la même figure 7.3), le vecteur vibrant n’a plus la possibilité de traverser entièrement ce second Nicol. Seule la projection de ce vecteur m'n', identifié par le segment pq (Fig. 7.3) sur le plan de polarisation du second Nicol, traverse ce dernier. On observe une extinction partielle de lumière : la grandeur du vecteur est alors donnée par le produit mn cos a, soit la longueur du segment pq. En poursuivant la rotation de ce Nicol, on observe une extinction complète du faisceau à un angle a de 90° suivie d’une récupération complète de son intensité lorsque l’angle atteint 180°, donc lorsque les plans de polarisation des deux prismes de Nicol seront de nouveau parallèles, pour un angle a quelconque, l'intensité de la lumière, proportionnelle au carré de la longueur du vecteur, varie comme cos2a. Ce système constitue la base du principe de fonctionnement du polarimètre.
|
|
Figure 7.3. Effet de la rotation du Nicol analyseur sur l’intensité de la lumière transmise.
c. Polarisation de la lumière diffusée - particules sphériques ou isotropes
De manière quasi automatique la lumière diffusée par des particules sphériques ou isotropes est complètement polarisée si la lumière incidente est polarisée. En d’autres termes, un système quel qu’il soit ne peut dépolariser une lumière polarisée. Si la lumière incidente est polarisée, la lumière diffusée l’est aussi.
Par contre, si la lumière incidente est de la lumière naturelle, c’est-à-dire non polarisée, la lumière diffusée est partiellement polarisée. Le plan de polarisation étant défini par la direction des rayons incidents et la direction d’observation, appelons H et V l’intensité de la lumière polarisée perpendiculairement et parallèlement au plan d’observation. Le rapport H/V est appelé facteur de dépolarisation. On peut montrer que ce facteur varie comme cos2q si q est l’angle entre la direction des rayons incidents et la direction d’observation. À angle droit du faisceau incident la polarisation est donc complète puisque cos q = 0 donc H = 0. Dans la direction du rayon incident cos2q = 1 et H = V; la lumière est donc naturelle. Entre les deux directions elle est partiellement polarisée (Fig. 7.4).
|
|
Figure 7.4. Observation de la diffusion de la lumière.
d. Polarisation de la lumière diffusée: particules anisotropes
La diffusion par particules anisotropes conduit à une relation entre le facteur de dépolarisation et q qui n’est plus aussi simple que la précédente. Cette relation inclut les caractéristiques géométriques de la particule. On peut donc déterminer le degré d’anisotropie d'une molécule en mesurant le facteur de dépolarisation. Cette propriété est utilisée dans le cas où l’on observe des molécules de géométries particulières comme, par exemple, des molécules polymériques en forme de bâtonnet. Ces applications sont évidemment bien de l’objet de ce module et on ne décrira pas ici les phénomènes et les propriétés qui leur sont associées.
7.3 Effet RAMAN - observation expérimentale
Ce phénomène a été prédit par Adolf SMEKAL en 1923, et théoriquement décrit par les fondateurs de la mécanique quantique (HEISENBERG en 1925, SCHRÖDINGER en 1926, DIRAC en 1927). Il a été observé expérimentalement par le savant hindou Sir Venkata Raman en 1928. Deux chercheurs russes, Grigori Landsberg et Leonid Mandelstam ont aussi observé indépendamment et presque simultanément cet effet. Malencontreusement, l’histoire n’a pas retenu que le nom de ces derniers. Cet effet, au contraire de la diffusion normale, fait intervenir les propriétés internes de la molécule. Examinons de plus près les phénomènes observables.
On éclaire une substance (diatomique ou poly atomique, mais pour le moment, nous ne traiterons ici que le cas de la molécule diatomique) latéralement au moyen d’une raie monochromatique très intense. On analyse au spectrographe la lumière diffusée perpendiculairement à la direction d’éclairement. En général, on utilise l’une ou l’autre des raies intenses visibles et ultraviolettes émises par l’arc au mercure : 253,7 nm, 404,7 nm ou 435,8 nm isolées au moyen d’un filtre approprié. On utilise aussi de plus en plus des raies émises par des lasers éclairant dans le visible, qui émettent une radiation beaucoup plus monochromatique (par exemple un laser à argon émettant à 514,5 nm).
Dans la lumière analysée, on trouve une raie dont la longueur d’onde est la même que celle de la radiation incidente. Cette raie est due à la diffusion normale dont il a été question plus haut.
En plus de cette raie, on en observe une autre beaucoup moins intense, décalée vers les grandes longueurs d’onde (Fig. 7.5). Si la raie excitatrice est très intense, et si on prend beaucoup de précautions pour diminuer l’intensité de la raie due à la diffusion normale, on observe de part et d’autre de celle-ci une série de raies très faibles approximativement équidistantes.
|
|
Dans le cas de HCl, l’intervalle de fréquence,
D![]() ,
entre la
raie décalée et la raie excitatrice est 2 886,0 cm-1.
Par ailleurs, les
raies équidistantes sont séparées par 41,6 cm-1 en moyenne. Remarquons tout de suite que si
l’on reprend les
constantes a, b et c qui entrent dans les formules expérimentales
des spectres de rotation et de vibration on constate pour HCl :
,
entre la
raie décalée et la raie excitatrice est 2 886,0 cm-1.
Par ailleurs, les
raies équidistantes sont séparées par 41,6 cm-1 en moyenne. Remarquons tout de suite que si
l’on reprend les
constantes a, b et c qui entrent dans les formules expérimentales
des spectres de rotation et de vibration on constate pour HCl :
2 a = 2 ´ 20,60 = 41,20 cm-1
D![]() = b -
c
= 2 937,30 -
51,60 = 2 885,70 cm-1
= b -
c
= 2 937,30 -
51,60 = 2 885,70 cm-1
Ces nombres sont si voisins des nombres tirés de l’effet RAMAN que l’on peut dire dès maintenant que la raie éloignée est certainement liée à la vibration de la molécule, les autres raies étant liées à la rotation.
Nous sommes donc en présence d’un effet de diffusion de la lumière dans lequel, il y a interaction entre la lumière incidente et la molécule. Puisqu’il y a variation de fréquence de la lumière diffusée, il y a échange d’énergie entre la radiation électromagnétique et la molécule. Au contraire, la diffusion normale se fait sans échange d’énergie.
On peut comparer ces deux phénomènes à une collision élastique et à une collision inélastique. En général, lors d’une collision élastique entre deux molécules, l’énergie cinétique totale est conservée. Dans la collision inélastique, il y a variation de l’énergie cinétique. Cette variation se fait au détriment (ou à l’avantage) d’autres formes d’énergie (par exemple, rotationnelle, vibrationnelle, potentielle). Nous verrons qu’il en est de même dans le cas de l’effet RAMAN.
7.4 Théorie de l’effet RAMAN
Considérons une onde
électromagnétique incidente de fréquence n donc porteuse d’énergie hc![]() .
L’onde peut céder une partie de cette énergie à la molécule; cette partie cédée peut être employée à faire passer la molécule de son
niveau fondamental vers l’un des niveaux excités. Si h c D
.
L’onde peut céder une partie de cette énergie à la molécule; cette partie cédée peut être employée à faire passer la molécule de son
niveau fondamental vers l’un des niveaux excités. Si h c D![]() est
l’énergie nécessaire, on aura une lumière diffusée d’énergie E, exprimée en cm-1, telle que :
est
l’énergie nécessaire, on aura une lumière diffusée d’énergie E, exprimée en cm-1, telle que :
(7.2)
E = ![]() -
D
-
D![]()
Comme D![]() ne peut prendre que des valeurs bien définies correspondant
aux sauts entre les niveaux d’énergie de la molécule, la lumière diffusée sera formée
de raies.
ne peut prendre que des valeurs bien définies correspondant
aux sauts entre les niveaux d’énergie de la molécule, la lumière diffusée sera formée
de raies.
Si la molécule passe du niveau de vibration u = 0 au niveau u = 1, l’énergie qu’il lui faut est :
| (7.3) | 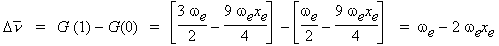 |
Cas de HCl : D![]() = we
-
2 wexe = 2 988,9
-
2
× 51,6 = 2 885,7 cm-1
= we
-
2 wexe = 2 988,9
-
2
× 51,6 = 2 885,7 cm-1
On retrouve la valeur du déplacement de la raie éloignée. Cette raie est donc bien due à un échange d’énergie avec transition de vibration. D’autre part, il y a diminution d’énergie de la radiation initiale, donc diminution de la fréquence, ce qui entraîne un déplacement vers les grandes longueurs d’onde.
La règle de sélection Du = ± 1 interdit pratiquement les sauts à des niveaux plus élevés que 1 à partir du niveau fondamental.
On peut se demander pourquoi on ne pourrait observer le processus inverse, processus qui serait une cession d’énergie de la molécule par exemple dans l’état u = 1 et passage de cette dernière à l’état u = 0. On devrait dans ce cas observer une raie vers les courtes longueurs d’onde, symétrique de la première. Cette raie n’est pas observable parce que la population du niveau u = 1 est très faible à la température ordinaire (Chapitre 6).
En effet, on peut montrer qu’à la température normale, le nombre de molécules diatomiques qui se trouvent avec une énergie correspondant au niveau de vibration u = 1 est de plusieurs ordres de grandeurs plus petits que le nombre situés sur le niveau u = 0. Pour trouver une population significative du niveau u = 1, il faut que l’énergie nécessaire pour atteindre ce niveau soit comparable à l’énergie disponible à la température de la molécule. On retrouve ce type de conditions, par exemple, dans le cas de la molécule d’iode I2 ainsi que dans certaines molécules plus complexes. Dans ces cas les 2 raies sont observables, la raie décalée vers les petites longueurs d’onde (ou vers des énergies plus élevées) est appelée raie anti-STOKES. Elle est toujours moins intense que la première qui a reçu le nom de raie STOKES (Fig. 7.6).
|
|
Figures 7.6. Transitions RAMAN de vibration et spectre schématique.
De son côté, le spectre de raies équidistantes (Fig. 7.6) est dû à des transitions avec échange d’énergie entre les niveaux de rotation. Comme plusieurs niveaux de ces sont peuplés à la température ordinaire, on observe des raies de chaque côté de la raie excitatrice.
|
|
Figures 7.7. Transitions RAMAN de rotation.
L’intervalle des raies est double de l’intervalle observé dans le spectre infrarouge car la règle de sélection est différente :
(7.4) DJ = 0, ± 2
En ignorant l’effet de la distorsion centrifuge ou encore en posant D = 0, l’énergie d’une raie quelconque est
F(J+2) - F (J) = B(J+2) (J+3) - B J(J+1)
(7.5) D(J+2,J) = F(J+2) - F(J) = 2 B(2J+3)
De la même manière, la différence d'énergie entre les niveaux J + 3 et J + 1 est :
D(J+3, J+1) = B(J+3) (J+4) - B(J+1) (J+2)
D(J+3, J+1) = 4 B J + 10 B = 2B(2J+5)
et l’intervalle entre deux raies successives est
(7.6) D(J+3, J+1) - D(J+2, J) = 2 B[(2J+5) - (2J+3)] = 4 B.
Cette relation permet d’obtenir la valeur de la constante de rotation B et donc de calculer les distances internucléaires (voir le tableau 3.2 du chapitre 3). De plus, avec un appareil de grande dispersion, en introduisant les paramètres relatifs à la distorsion centrifuge, les formules sont plus compliquées (Chapitre 5.4), on peut aussi obtenir théoriquement les valeurs des constantes de distorsion centrifuge D (Tableau 7.1).
Tableau 7.1. Quelques
caractéristiques physiques de molécules diatomiques homonucléaires
Molécule |
B
|
re |
D (cm-1) |
D / B |
H2 |
60,853 |
0,074 144 |
0,0471 |
7,74 10-4 |
14N2 |
1,998 24 |
0,109 768 |
5,76 10-6 |
2,882 10-6 |
14N º15N |
1,9238 |
|
|
|
| 15N º15N | 1,8577 | |||
16O2 (u = 0) |
1,437 68 |
0,120 752 |
4,839 10-6 |
3,366 10-6 |
|
16O2 (u = 1)* |
1,4219 |
4,623 10-6 | 4,623 10-6 | |
| 16O=17O | 1,3953 | 4,303 10-6 | 4,303 10-6 | |
| 16O=18O | 1,3579 | 4,965 10-6 | 4,965 10-6 | |
16O2 (a1Dg)** |
1,4264 |
0,121 563 |
4,86 10-6 |
3,40 10-6 |
| Cl-Cl | 0,244 | 0,198 79 | 1,86 10-7 | 0,762 10-6 |
35Cl-37Cl |
0,2365 |
|
|
|
* : état vibrationnel; ** : état électronique excité.
Ce tableau confirme bien qu’en général la constante de distorsion centrifuge est négligeable devant la constante de rotation B.
7.5 Polarisation des raies RAMAN
Comme dans le cas de la diffusion RAYLEIGH, la lumière diffusée par les molécules due à l’effet RAMAN peut être polarisée. Dans ce cas, la polarisation est liée non pas à l’anisotropie de la molécule elle-même, mais à l’anisotropie de la vibration. Si la vibration possède la symétrie sphérique la raie de vibration n’est pas polarisée. Elle l’est si la vibration n’est pas symétrique. Les vibrations de molécules diatomiques étant toujours symétriques, les raies ne sont pas polarisées. Nous reverrons ce problème dans le cas des molécules polyatomiques.
7.6 Condition nécessaire à l’obtention de raies RAMAN - polarisabilité d’une molécule
La variation de moment dipolaire de la molécule est une condition nécessaire pour qu’un saut puisse se faire entre deux niveaux par absorption ou émission spontanée, que ce soit en rotation (Chapitre 3) ou en vibration (Chapitre 4).
Mais dans le cas de l’effet RAMAN, ce qui est requis est une variation, non pas du moment dipolaire, mais plutôt de la polarisabilité de la molécule
Si on soumet cette molécule à un champ électrique, on va assister à une déformation du nuage électronique due à l’action du champ. Cette déformation entraîne l’apparition d’un moment dipolaire (moment dipolaire induit). Une radiation électromagnétique possède un champ électrique et produit donc l’effet précédent; ce dernier est proportionnel à la polarisabilité de la molécule.
Or, le nuage électronique n’a pas la exactement la même forme pour différents niveaux de vibration. On peut imaginer que sa tendance à se déformer sera également différente. C'est le phénomène qui constitue une variation de polarisabilité de la molécule.
En raison de leur symétrie, les molécules diatomiques homo nucléaires ont un moment dipolaire nul. Cependant leur polarisabilité varie avec le niveau d’énergie de vibration. Bien qu'elles n’absorbent pas dans l'infrarouge, ces molécules présentent un spectre Raman, tout comme les molécules hétéro nucléaires.
7.7 Spectre RAMAN et spectre d’absorption infrarouge
On pourrait croire qu’on obtient les mêmes informations à l’aide des bandes d’absorption de vibration pure et des raies RAMAN de vibration. C’est partiellement vrai pour les molécules poly atomiques. Pratiquement, le spectre de rotation RAMAN étant difficile à observer, il est peu utilisé et le spectre de rotation pure ou de rotation-vibration reste la meilleure source d’informations. L’effet RAMAN constitue cependant un complément non négligeable dans l’étude des structures puisque certaines transitions ne sont pas actives en absorption infrarouge (molécules diatomiques homo nucléaires par exemple) et qu’elles le sont en Raman. L’inverse est aussi vrai : certaines transitions actives en spectroscopie infrarouge ne le sont pas en Raman. Le cas des molécules poly atomiques sera repris dans un module ultérieur.
Pour les molécules diatomiques et hétéro nucléaires, la détermination des fréquences de vibration peut se faire par l’une ou l’autre des deux méthodes, complémentaires, la spectroscopie RAMAN présentant des avantages et des inconvénients par rapport à la spectroscopie infrarouge.
a. Avantages du spectre RAMAN sur le spectre d’absorption infrarouge
- Certaines vibrations sont inactives dans l’infrarouge et actives en RAMAN (cas des molécules homo nucléaires diatomiques).
- Le spectre RAMAN se trouve dans une région spectrale (le visible ou l’ultraviolet) plus facile à étudier. En fait, on peut le placer dans la région spectrale que l’on veut.
- L’appareillage est moins coûteux, bien que l’introduction, là aussi de l’informatique, a atténué cet avantage.
b. Inconvénients du spectre RAMAN
- A priori, toutes les molécules sont susceptibles d’effet RAMAN. Toutefois, les limites de la sensibilité (liées à la dispersion des spectrographes utilisés dans le visible) et dans la précision des observations reliées à cet effet entraînent un nombre d'applications plus restreint.
- Expérimentalement, on observe de grandes difficultés dans la mesure d’intensité des raies. Comme celles-ci donnent accès à des informations sur la concentration des espèces, on conçoit que l’effet Raman ne constitue pas une approche généralisée ayant cet objectif.
- Structure de rotation difficile à obtenir, ceci étant du à la présence d’une forte diffusion RAYLEIGH et aux caractéristiques des sources lumineuses utilisées, bien que l’introduction de sources lasers monochromatiques a permis d’accroître sensiblement les performances des appareils RAMAN, à ce chapitre. Cependant, l’introduction de l’informatique a entraîné, de manière concomitante, une augmentation des coûts.
|
L’effet
Raman, un processus de
diffusion de la lumière par les molécules, obéit à des exigences et donc
des lois, différentes de celles qui s’appliquent en absorption ou en émission. C’est la
variation de polarisabilité de la molécule qui gouverne ce processus. Les règles de
sélection sont modifiées et l’on a accès dans certains cas à des informations non disponibles en
spectroscopie infrarouge. |
1. Les intervalles entre les niveaux d’énergie de vibration de H2, HD et D2 peuvent être estimés à partir des spectres de diffusion Raman. Ils mesurent respectivement 4 401,2, 3 813,1 et 3 115,5 cm-1. Calculez la constante de force dans les systèmes CGS et SI du ressort physique équivalant pour les trois espèces isotopiques mentionnées de l’hydrogène.
Rép. : k = 570,9 N•m-1 pour la molécule H2.
2. Lorsque l’acétylène est irradié à 435,83 nm une raie RAMAN attribuée à l’élongation longitudinale symétrique est observée à 476,85 nm. Calculez la fréquence fondamentale, en Hz et l’énergie en cm-1 de cette vibration.
Rép. : l Raman = 273,68 nm.
3. Lorsque HCl est irradié avec la raie du mercure située à 253,65 nm, indiquez en nm où l’on doit retrouver la raie Stokes correspondant à la transition de vibration pure, u = 0 ® u = 1? On donne pour HCl : we = 2 990,9 cm-1 et wexe = 52,8 cm-1 .
Pour en savoir plus
Sur le web :
En complément à ces notes de cours, visitez un site (module 4) : http://benhur.teluq.uquebec.ca/~mcouture/Fodar99/modules.htm. Malheureusement, avec les changements technologiques sensées améliorer les TIs, les animations ne sont plus accessibles (2020-11-16)..
On trouve aussi un site interactif préparé par le professeur Marc Couture, de la TÉLUQ (Montréal), site qui permet de mettre en relief divers modes de rotation et de vibration de 24 molécules allant de molécules biatomiques jusqu'au méthane : http://benhur.teluq.uquebec.ca/~mcouture/Fodar99/Hzdemo.htm (visité le 25 février 2019).
Une série de biographies dont celle de Sir C. V. Raman : http://biography-of.com/c-v-raman (visité le 2021-06-02).
Rappel: on peut toujours consulter les biographies disponibles sur Wikipedia...
Un site général en physique qui contient beaucoup d’information sur de nombreux phénomènes physiques. On trouvera en particulier à l’adresse indiquée des présentations sur la diffusion RAYLEIGH, ou «Pourquoi le ciel est bleu ?»
Contact : Carl R. (Rod) Nave, Dept of Physics and Astronomy, Georgia State University, Atlanta, Georgia, 30303-3083 :http://hyperphysics.phy-astr.gsu.edu/hbase/atmos/blusky.html (visité le 2021-06-02).
Il faut ajouter que ce site peut être avantageusement utilisé comme glossaire, en anglais bien sûr.
Dernière mise à jour : 2021-07-02.
x x x x x x x x x x x