 |
LES ISOTOPES
|
Puisqu’un noyau portant un nombre précis de protons peut avoir un nombre variable de neutrons (les isotopes), il a plusieurs questions qui demandent des réponse. Question : Objectifs: |
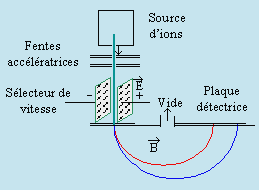
La découverte des isotopes résulte de l’analyse des rayons canaux par la méthode de déflexion électrique et magnétique. Par la méthode de la parabole, J. J. THOMSON (1913) fut le premier à mettre en évidence ce nouveau phénomène. ASTON perfectionna cette méthode et il peut être considéré comme l’inventeur du spectrographe de masse. La source d’ions est toujours constituée par les rayons canaux, mais les champs électriques et magnétiques sont placés de telle sorte que les ions de même valeur e/m sont focalisés sur une courte raie quelle que soit leur vitesse (d’où le nom de spectrographe).
Les spectrographes modernes utilisent différentes sources d’ions. Les plus anciennes et encore les plus nombreuses sont constituées d’un faisceau d’électrons croisant à angle droit le faisceau atomique ou moléculaire. L’ionisation se produit par choc: c’est de l’ionisation électronique. Dans ce cas on peut contrôler l’énergie des électrons en contrôlant leur vitesse. De façon standard, le potentiel d’accélération de ces électrons est fixé à 70 eV, bien que sur les appareils plus sophistiqués on peut aussi contrôler et ajuster à volonté ce potentiel. Dans le cas d’un faisceau atomique, puisque les divers atomes n’ont pas la même énergie d’ionisation , on pourra les différencier à la fois par le potentiel d’apparition des ions et leur valeur e/m. On trouve aussi maintenant des faisceaux constitués d’ions positifs tels que H3+, CH5+, tert-C4H9+, etc. Dans ces cas, la fragmentation des ions moléculaires est en général beaucoup moins importante. En effet, les ions résultent plutôt du transfert d’un proton et non d’un choc entre un électron accéléré. Les énergies ainsi libérées en ionisation chimique sont moins grandes. Ainsi, le spectre de masse est susceptible de contenir un signal plus important correspondant à la masse moléculaire augmentée d’une unité :
RH+ + M ® R + MH+
Dans le cas de molécules ayant la même masse moléculaire, comme par exemple l’oxyde de carbone, l’azote et l’éthylène à la masse 28, on fait appel à des appareils capables de très haute résolution. (Voir plus loin, les masses exactes des noyaux).
 |
Spectrographe de BAINBRIDGE
|
|
Spectrographe d’ASTON
Figure 14.1. Spectrographes de masse.
2. La règle du nombre entier
Les valeurs des différentes masses des atomes sont comparées à celle de l’isotope 12 de l’atome de carbone. La précision des mesures d’ASTON était de 1 pour 1 000. Il découvrit que le néon, de poids atomique chimique 20,20, mesuré par des méthodes chimiques moins subtiles, était en fait composé de trois isotopes de poids atomiques 20,00, 21,00 et 22,00. Les intensités des raies correspondantes étaient 9 pour l’élément 20, 1 pour l’élément 22 et pratiquement 0 pour l’élément 21. Il put donc montrer que le poids atomique chimique correspondait bien au mélange dans la proportion 9 pour 1 des néons 20 et 22.
ASTON a pu faire la même démonstration pour d’autres éléments dont les poids atomiques chimiques n’étaient pas entiers. Il trouva des nombres d’isotopes élevés pour certains éléments : 10 pour l’étain, 9 pour le xénon,... Il montra également que les éléments dont le poids atomique chimique est un nombre entier ne possèdent pas d’isotope : c’est le cas du fluor, du sodium, de l’aluminium,... ou bien possèdent des isotopes très rares comme dans le cas de l’hélium. Actuellement, on connaît environ 300 isotopes stables. Le nombre d’isotopes instables - voir plus loin le chapitre sur la radioactivité- est encore plus grand.
La règle du nombre entier qui conclut ces expériences exprime que tout élément dont le poids atomique chimique diffère d’un nombre entier, résulte d’un mélange d’isotopes, chacun d’eux ayant un poids atomique mesuré par un nombre entier.
Dès 1815, PROUST nota que les poids atomiques avaient une préférence marquée pour les valeurs entières. Il émit l’hypothèse que les atomes de tous les éléments sont construits avec la même particule fondamentale, probablement l’hydrogène, le plus léger de tous les atomes. À mesure que les masses atomiques furent connues de façon plus précise cette hypothèse devint insoutenable puisque les valeurs entières sont des exceptions.
L’expérience et les conclusions d’ASTON donnèrent une vie nouvelle à l’hypothèse de PROUST. Mais le problème de la détermination de la particule élémentaire se heurta à une autre difficulté: les écarts à la règle du nombre entier. On verra comment plus tard expliquer ces écarts.
La précision des spectrographes de masse s’est améliorée de façon telle qu’il est possible de déterminer les masses avec cinq chiffres significatifs. Cette précision est si élevée que l’on peut séparer 2H et 1H2 (l’atome de deutérium et la molécule d’hydrogène) qui ne diffèrent que par une différence de masse infime. En prenant arbitrairement pour poids atomique de référence l’atome de carbone 12, (12C), les masses des éléments les plus légers de la classification périodique apparaissent au tableau 14.2.
Le choix de la référence
On aurait pu penser créer une table des masses atomiques des éléments chimiques à partir de l’atome d’hydrogène. Cet élément chimique moléculaire à l’état naturel, n’était guère d’usage facile. Pour leur part, les gaz rares, justement à cause de leur rareté, ne constituaient pas non plus une référence appropriée. L’oxygène, bien que moléculaire, constituant stable, généreusement distribué et donc accessible fut rapidement utilisé par les chimistes de tous les pays et cela jusque en 1961. Avec cette référence, l’hydrogène atomique avait une masse de 1,008. L’oxygène est formé de trois isotopes stables :
- 16O (8 neutrons, 8 protons) 99,759 %
- 17O (9 neutrons, 8 protons) 0,037 %, et
- 18O (10 neutrons, 8 protons) 0,204%.
Les physiciens proposaient de donner la masse 16 non pas à l’oxygène naturel mais bien plutôt à l’oxygène16. Il y avait donc une différence importante entre l’échelle des chimistes et celle des physiciens (tableau 14.1a). On chercha à se mettre d’accord. En 1957, ORLANDER et NIER proposèrent plutôt d’utiliser le carbone12 comme référence. En effet, la séparation de cet élément était devenu plus facile que celle de l’oxygène16, le carbone étant en outre un constituant universel d’une famille sans limite de composés. Ce choix fut ratifié en 1960 à Ottawa par l’Union internationale de physique et en 1961 à Montréal par l’Union internationale de chimie pure et appliquée (IUPAC).
Tableau 14.1. Échelles comparées des références pour les masses atomiques
| Élément | Échelle des chimistes |
Échelle des physiciens |
Nouvelle échelle commune (1961) |
| Onat | 16,000 00 | 16,004 4 | 15,999 4 |
| 16O | 15,995 | 15,994 91 | 15,994 91 |
| Cnat | 12,010 | 12,015 0 | 12,011 15 |
| 12C | 12,000 52 | 12,003 82 | 12,000 00 |
| Hnat | 1,008 0 | 1,008 28 | 1,007 97 |
| 1H | 1,008 0 | 1,008 131 | 1,007 796 |
| Tiré de Denis-Papin, M. et J. Castellan, Métrologie générale, tome II, Dunod, Paris (1971). | |||
Tableau 14.1a. Masse des isotopes naturels légers stables
| Noyau | Masse | Noyau | Masse | Noyau | Masse |
| 1n | 1,008 665 | 11B | 11,009 305 | 19F | 18,998 405 |
| 1H | 1,007 825 | 12C | 12,000 000 | 20Ne | 19,992 436 |
| 2H | 2,014 102 | 13C | 13,003 355 | 21Ne | 20,993 843 |
| 3He | 3,016 029 | 14N | 14,003 074 | 22Ne | 21,991 383 |
| 4He | 4,002 603 | 15N | 15,000 109 | 23Na | 22,989 768 |
| 7Li | 7,016 003 | 16O | 15,994 915 | 24Mg | 24,985 042 |
| 9Be | 9,012 186 | 17O | 16,999 131 | 25Mg | 24,985 837 |
| 10B | 10,012 937 | 18O | 17,999 160 | 26Mg | 25,982 594 |
| http://www.webelements.com/ | |||||
Les poids atomiques chimiques sont aussi nettement reproductibles que la précision des mesures, à tel point qu’avant la découverte des isotopes ces nombres étaient considérés comme des constantes fondamentales. Maintenant, nous savons que le principal facteur déterminant le poids atomique chimique est l’abondance relative des divers isotopes (Tableau 14.1b). La mesure de l’abondance relative combinée avec les poids atomiques physiques des isotopes fournit une détermination extrêmement précise des poids atomiques chimiques. Ces faits montrent que l’abondance relative est une constante rigoureusement suivie par la Nature. Les analyses de météorites montrent que cette constance n’est pas uniquement terrestre mais universelle et donc qu’elle est liée au processus de création du monde : voir Fig. 14. 2.
Tableau 14.1b. Abondance des isotopes naturels légers stables
| Noyau | % | Noyau | % | Noyau | % |
| 1H | 99,9885 | 12C | 98,93 | 20Ne | 90,48 |
| 2H | 0,0115 | 13C | 1,07 | 21Ne | 0,27 |
| 3He | 0,000 137 | 14N | 99,632 | 22Ne | 9,25 |
| 4He | 99,999 863 | 15N | 0,368 | 23Na | 100 |
| 7Li | 92,41 | 16O | 99,757 | 24Mg | 78,99 |
| 9Be | 100 | 17O | 0,038 | 25Mg | 10,00 |
| 10B | 19,9 | 18O | 0,205 | 26Mg | 11,01 |
| 11B | 80,1 | 19F | 100 | ||
| http://www.webelements.com/ | |||||
|
|
Figure 14.2a. Isotopes naturels de quelques corps simples.
|
|
Figure 14.2b. Isotopes naturels de quelques corps simples.
Il y a cependant quelques exceptions à cette loi. Par exemple, on observe également une légère variation dans le rapport D/H (2H/1H) de l’eau entre les eaux de surface des océans et le fond des fosses océaniques. Il existe un léger gradient de concentration en atomes lourds lorsque ce rapport est mesuré à des profondeurs de plus en plus grandes. Dans les synthèses biologiques, il apparaît de fines différences dans les rapports isotopiques. Cette propriété est parfois utilisée pour identifier l’origine de certains produits dont on doute de la provenance. Par exemple, l’origine d’artefacts industriels de l’époque gréco romaine et mis à jour par les archéologues, peut être certifiée en mesurant les rapports isotopiques du plomb. Des échantillons de plomb provenant de lieux différents présentent des abondances isotopiques différentes. Le plomb est l’élément terminal des séries radioactives naturelles et l’abondance relative de ses isotopes dépend de la nature du minerai radioactif primaire (voir le chapitre suivant, 15.9). Ainsi, les objets fabriqués dans différentes contrées ou îles de la région méditerranéenne ont des rapports 207Pb/206Pb, 206Pb/204Pb et 207Pb/206Pb qui varient avec l’origine du minerai, source du métal (Fig. 14.3).
|
|
Figure 14.3. Rapports isotopiques du plomb dans différents minerais situés en Méditerranée centrale.
(Grèce continentale : Othrys, Essimi, Lavrion; Îles grecques : Kythnos, Thasos, Chypre).
Certains isotopes sont très rares (en termes de concentration): 2H : 0,02 %, 13C : 1,1 %, 15N : 0,4 %, 17O : 0,04 %, 18O : 0,20 %, 46Ca : 0,003 %, 235U : 0,7 %, ...
Le cas du rapport isotopique 13C/12C
Des analyses en spectrométrie de masse de très haute précision permettent d’observer et de mesurer des différences extrêmement fines dans le rapport isotopique 13C/12C des composés organiques. Ce rapport en effet varie en fonction des divers paramètres tels que le mode de synthèse du produit selon son origine animale, végétale, marine,... La figure 14.4 montre que si ce rapport est inférieur à 1,085 pour les combustibles fossiles, il se situe plutôt entre 1,094 et 1,111 pour les carbonates terrestres. Détails fort intéressants ou intrigants, il semble que le CO2 de la respiration humaine soit plus riche en 13C chez les américains comparativement à celui des européens et le sucre provenant de la betterave à sucre est légèrement plus pauvre 13C que celui extrait de la canne à sucre.
|
|
Figure 14.4. Exemples de déviation naturelle de 13C.
(Tiré de Meier-Augenstei, W.n, LC•GC, 15(3), 244 (mars 1997)).
Cette figure montre aussi certaine de ces variations. Ainsi, le rapport 13C/12C se situe entre 1,055 et 1,111 pour une grande variété de produits. Les variations extrêmes sont donc très faibles, le rapport 13C/12C ne variant tout au plus que de 6 % et à l’intérieur de produits particuliers, la variation est le plus souvent inférieure à 1 %. Dans le cas des plantes terrestres, cette variation est au plus de 0,033 %. C’est donc dire l’extrême sensibilité requise des spectromètres de masse. À cette échelle limitée, on a substitué une notation d 13C [‰] :
![]()
Dans cette égalité, R = 13C/12C. La valeur Rstandard est celle d’un échantillon d’un carbonate de calcium (belemnite) extrait de la formation Pee Dee en Caroline du sud: RPDB = 0,0112372 ± 0,000009, ce qui est équivalent à une abondance de 1,1112328 ‰ en 13C. La figure 14.4 montre combien l’échelle ainsi constituée est plus simple de lecture.
Dans le cas d’un composé organique, le principe de la méthode de mesure de ce rapport consiste tout d’abord à transformer le carbone en CO2 puis d’injecter ce CO2 dans le port d’entrée d’un spectromètre de masse et de calculer les rapports en mesurant les pics observés aux masses 44 et 45. Le couplage chromatographe à gaz - spectromètre de masse isotopique (CG/SMI) est une méthode très puissante d’analyse des mélanges complexes. Par exemple, à la sortie d’un chromatographe à gaz, les produits sont acheminés sur un micro-four contenant un mélange oxyde de nickel + palladium ou le précédent mélange enrichi d’oxyde de cuivre chauffé vers 900 ºC.
La valeur du rapport 13C/12C renseigne sur les différents processus biochimiques et physiologiques que génère la photosynthèse des plantes. Si le mécanisme de fixation du CO2 est le même pour toutes les plantes, celui de son extraction de l’atmosphère se déroule selon trois processus :
Dans chaque cas les teneurs en 12C et 13C sont différentes. Le cycle de Calvin produit des déviations isotopiques d13C allant de – 23 à – 30 °/°° et pour le cycle de Hatch Slack allant de –9 à –13 °/°° . On peut donc, par exemple, détecter aisément l’ajout de sucre de canne dans les jus de fruits. L’analyse isotopique de l’hydrogène et de l’oxygène permet de reconnaître le cycle de l’eau.
D’autres extensions ont été faites vers les isotopes de l’hydrogène, de l’oxygène,...
Les teneurs en isotopes de l’oxygène et de l’hydrogène sont exprimées en ‰ par rapport à la référence SMOW (Standard Mean Ocean Water).
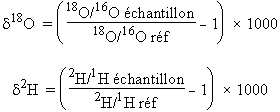
La valeur de la référence du standard international est telle que : 18O/16O = 0,200 52 % et 2H/1H = 155,76 ppm.
Le rapport isotopique 18O/166O mesurés dans du matériel végétal est particulièrement sensible aux conditions climatiques qui ont prévalu pendant la croissance de la plante. Par exemple la déviation isotopique mesurée dans le vin peut varier de –1,9 (écart type 0,2) à + 2,0 (écart type 0,5) entre deux années successives pour la production du même vin dans la même propriété. On voit donc qu’il est pratiquement possible de distinguer non seulement la région de production mais aussi l’année de production.
Le cas du rapport isotopique 15N/14N
L’appareillage a été quelque peu modifié pour mesurer le rapport isotopique des masses 14N et 15N. Dans ce cas le four contient un fil de cuivre chauffé à 600 ºC. Les oxydes d’azote sont alors réduits en azote. Pour éviter les interférences des ions CO+ à la masse 28 et 13C16O+ à la masse 29, l’effluent gazeux passe sur un piège refroidi à l’azote liquide pour piéger le gaz carbonique avant d’être acheminé vers le spectromètre de masse. La valeur de la référence du standard international est telle que : 15N/14N = 0,367 65 %.
Les premières applications ont été effectuées sur des substances pures isolées. Le couplage du spectromètre de masse à la chromatographie gazeuse a notablement facilité et amélioré les mesures de déviations isotopiques. La mise en œuvre des techniques multiplie les possibilités et les performances.
Exemple d’application Cas de la vanilline
À cause du prix élevé de la vanilline (Fig. 14.5), son adultération avec une vanilline de synthèse pose de sérieux problèmes pour le commerce de ce produit. La vanilline peut être synthétisée à partir de la lignine, de l’eugénol, du guaïacol; dans ces trois cas la valeur d13C est inférieure à –26 ‰ alors qu’il est compris entre -16 et –21 ‰ pour la vanilline naturelle. L’adultération de la vanilline peut être réalisée par :
- ajout de vanilline de synthèse,
- ajout de vanilline de synthèse enrichie en [méthyle-13C] ou [carbonyle-13C].
Le couplage permet de déjouer ces contrefaçons (Tableaux 14.2 et 14.3).
|
|
Figure 14.5. La vanilline.
Tableau 14.2. Analyse isotopique (13C) de la vanilline naturelle, synthétique et "simulée naturelle"
| Échantillon | d 13CPDB (total) | d13CPDB* (méthyle) |
| vanilline de vanille (Madagascar) | -21,4* | -23,3 à -24,3, moyenne : -24,0 |
| vanilline (synthétique) de lignine | -27,3 | -28,2 à -28,8, moyenne : -28,4 |
| * 4 échantillons. | ||
Tableau 14.3. Analyse isotopique de la fonction carbonyle
de la vanilline
de différents extraits de vanille
| Échantillon | d13Ccarbonyle | Remarques |
| lignine | -37,7 ± 1,4 | vanilline de lignine connue |
| lignine altérée | +22,0 ± 0,6 | vanilline de lignine avec addition de [carbonyle-13C] vanilline |
| Bourbon* | -23,2 à -29,9 | vanilline naturelle connue |
| commercial | -42,8 à -43,1 | d13CMéthyle = +16,0 adultéré en méthyle-13C |
| commercial | -24,5 | Probablement naturel |
| commercial | + 67,1 | d13CTotal = -15,6 adultéré en carbonyle-13C |
| * 5 échantillons. Tiré de Chalchat, J. Cl. et R. Ph. Garry, Actes du colloque "Produits naturels d’origine végétale", 211, 18-24 octobre 1995, Saint-Jean-sur-Richelieu, Québec. | ||
Les éléments tels le carbone et
l’azote sont aisément analysables par les techniques de spectrométrie de
masse. Les molécules sont oxydées en gaz carbonique ou en oxydes
d’azote respectivement. Les
oxydes d’azote sont ensuite réduits en diazote. On
mesure donc les rapports 13CO2/12CO2
et 15N14N/14N14N.
On obtient donc les rapports isotopiques
13C/12C
et 15N/14N
de l’ensemble de la molécule. La
mesure isotopique du rapport 2H/1H
s’obtient directement sans transformation de la molécule par résonance magnétique
nucléaire. On peut donc mesurer
dans ce dernier cas le rapport isotopique non pas de la molécule entière mais
de parties de la molécule (Fig. 14.6). Les
techniques de mesure de résonance magnétique du carbone-13 permettent aussi
ce genre de mesures.
|
|
Figure 14.6. Abondances isotopiques de la vanilline naturelle mesurées par RMN-2H et exprimées en ppm..
4. Spectres atomiques des isotopes
On a vu (Chapitre 5.5) que la constante de RYDBERG dépend de la masse du noyau. Ceci est vérifié expérimentalement pour H, He+, Li++, Be+++ dont les spectres sont analogues à ceux de l’hydrogène, mais dont la position des raies est légèrement différente. De même, les spectres de 1H et 2H sont légèrement différents. Ce sont d’ailleurs les satellites observés au voisinage des raies de la série de BALMER qui ont amené la découverte du deutérium. Les valeurs calculées et mesurées des fréquences des raies des deux éléments sont en excellent accord et confirment les hypothèses de BOHR (Tableau 14.4).
L’effet isotopique sur les raies existe également pour les atomes plus compliqués. Il est difficilement calculable et il est même difficile à mettre en évidence car la séparation des raies est très petite.
Tableau 14.4. Décalage entre les raies émises par les atomes d’hydrogène et de deutérium
| Ha | Hb | Hg | Hd | |
| Séparation mesurée (cm-1) | 1,79 | 1,33 | 1,19 | 1,12 |
| Séparation calculée | 1,787 | 1,323 | 1,182 | 1,117 |
5. Séparation des isotopes
a) Spectrographie de masse
La séparation est complète, mais de petites quantités seulement peuvent être obtenues. La première bombe atomique a cependant été fabriquée à partir d’uranium 235 séparé par cette méthode.
b) Distillation fractionnée
Selon la théorie une molécule légère doit s’évaporer plus vite qu’une molécule lourde. ASTON essaya en vain de séparer les isotopes du néon par distillation fractionnée à partir du charbon actif refroidi à la température de l’azote liquide. UREY obtint pour la première fois du deutérium par distillation de l’hydrogène liquide. Cette méthode est lente et ne peut conduire à une séparation complète.
La distillation cryogénique du CO à –192 °C est une technique très utilisée pour obtenir le carbone-13.
c) Électrolyse
UREY montra (1934) que les échantillons d’eau prélevés dans les cellules électrolytiques étaient plus riches en eau lourde que les échantillons naturels. Cette observation a été à la base de la fabrication industrielle de l’eau lourde et du deutérium. Plusieurs électrolyses successives sont nécessaires pour atteindre une séparation à peu près complète. On utilise l’eau contenant NaOH (0,5 N) entre électrodes de nickel. À chaque étape d’électrolyse, on neutralise NaOH par le CO2 et on enlève le carbonate. On mélange ensuite l’eau obtenue avec la solution fraîche pour ramener la concentration de NaOH à une valeur convenable. Le tableau 14.5 résume les étapes successives. Bien que quelques essais aient été tentés avec succès pour séparer d’autres isotopes avec cette méthode, elle est pratiquement limitée à la séparation de l’eau lourde.
d) Diffusion thermique
Si un mélange gazeux est placé dans un récipient, le processus habituel de diffusion tend à uniformiser le mélange. Si, dans le récipient on produit un gradient de température, le constituant le plus léger se concentrera dans les zones les plus chaudes et le constituant le plus lourd dans les zones les plus froides. Un équilibre est atteint lorsque la séparation par unité de temps produite par le gradient thermique est égale au mélange produit par diffusion ordinaire. On opère dans des colonnes cylindriques longues et minces avec un fil chaud central en régime continu. On a pu atteindre une séparation de 99,4 % de H37Cl dans le HCl ordinaire avec une série de cinq colonnes de 6 mètres de longueur et de 8 mm de diamètre.
Tableau 14.5. Préparation de l’eau lourde par électrolyse de l’eau naturelle
| Étapes | Volumes
(L) de solution électrolysée |
Densité | Concentration en deutérium du résidu |
| 1 2 3 4 5 6 7 |
2 300 340 52 10 2 0,42 0,08 |
0,998 0,999 1,001 1,007 1,031 1,098 1,104 |
0,1 % 0,5 2,5 8,0 30,0 93,0 99,0 |
e) Diffusion à travers une paroi poreuse
La vitesse de diffusion d’un gaz à travers une paroi poreuse est donnée par la loi de GRAHAM. Elle est proportionnelle à l’inverse de la racine carrée de sa masse moléculaire. Les pores de la paroi doivent être petits comparés au libre parcours moyen des particules. Les particules légères qui ont une vitesse plus rapide, donc rencontrent plus fréquemment les trous, s’échappent plus rapidement. Cette méthode est actuellement la plus utilisée pour la séparation de l’uranium 235 à l’état d’hexafluorure UF6. On démontre cette loi de GRAHAM de façon simple. La théorie cinétique des gaz montre que pour un nombre n1 de molécules d’un gaz 1 et de masse m1, le produit PV est tel que :
PV = 1/3 n1 m1 u12
Dans cette équation u1 est la vitesse moyenne quadratique des molécules. Pour deux molécules qui ne diffèrent que par leur masse, on peut écrire :
PV = 1/3 n1 m1 u12 = 1/3 n2 m2 u22

Si n1 = n2, le rapport de diffusion est proportionnel à l’inverse de la racine carrée des rapports des masses individuelles des atomes ou des molécules diffusant à travers un orifice, il est aussi proportionnel à l’inverse de la racine carrée des masses molaires.
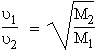
|
|
Figure 14.7. Préparation photochimique de l’eau lourde.
f) Photochimie infrarouge
En 1985, une équipe de chercheur du C.N.R.C., à Ottawa, a mis au point une méthode photochimique infrarouge compétitive sur le plan économique (Fig. 14.7). Cette méthode concerne la production de deutérium. Le réacteur CANDU demande une quantité importante d’eau lourde D2O. Cela concerne environ 90-95 % du coût d’immobilisation et environ 16 % du coût total. Le principe de la séparation est simple : il est basé sur la grande spécificité des spectres infrarouges de CF3D et CF3H vers 10,2 mm. Dans un premier réacteur l’eau naturelle est mélangée avec du trifluorométhane pauvre en deutérium. Il se forme un mélange de CF3D et CF3H. Ce mélange est acheminé vers un photoréacteur où un laser à CO2 provoque la décomposition sélective du CF3D :
(a) CF3H + HDO ® CF3D + H2O
(b) CF3D + 28 hn ® DF + :CF2
réaction suivie de (c) 2 :CF2 ® C2F4.
Le mélange de DF, de tétrafluoroéthylène et de trifluorométhane qui n’a pas réagi, est acheminé vers une chambre de séparation chimique. En présence de fluorure de sodium le DF est complexé sous forme de NaDF2. Plus tard, par voie thermique le DF est récupéré et acheminé vers la préparation de l’eau lourde. Quant au trifluorométhane appauvri en sa composante deutériée, il est retourné au réacteur initial et le cycle recommence. La réaction d’échange isotopique (a) est lente et est catalysée par de la soude, NaOH, et de diméthylsulfoxyde.
Comparativement à la méthode utilisant l’électrolyse de l’eau, le procédé photochimique présente des avantages certains. La méthode électrolytique repose sur le fait que l’électrolyse de H2O est plus rapide que celle de HDO. On récupère le reliquat qui n’a pas été électrolysé. Le tableau 14.5 montre que l’on a du électrolyser quelque 30 tonnes d’eau pour obtenir 1 kg d’eau lourde. En photochimie, on a plutôt décomposé le CF3D (donc indirectement HDO) pour obtenir l’eau lourde. En théorie, on photolyse 1 kg d’eau lourde HDO pour obtenir 1 kg de HDO. Bien sûr le rendement énergétique de la photochimie (l’usage du laser à CO2) est beaucoup moins élevé que celui de l’électrolyse. On traite cependant des quantités beaucoup moins importantes d’eau naturelle en procédé photochimique.
g) Réaction chimique
La
vitesse des réactions chimiques est affectée par la masse des particules,
groupes d’atomes,… qui sont transférées d’un réactif à un autre.
Par exemple, le transfert d’un proton en résonance dans la réaction
suivante est plus rapide que le même transfert d’un deutéron :
| (CH3)2(CD 3)C+ + CH2=C(CH3)2 | CH2=C(CH3) (CD3) + (CH3) 3C+ | |
| (CH3)2(CD 3)C+ + CH2=C(CH3)2 | CD2=C(CH3)2 + (CH3)2(CH2D) C+ |
En plus du facteur statistique (6 atomes d’hydrogène pour 3 atomes de deutérium), le deutéron étant deux fois plus lourd que celui d’hydrogène, le transfert du proton H+ est plus rapide que celui du deutéron D+ (voir par exemple le cours de «Cinétique chimique», chapitre II, équation 2.5). Par ailleurs, la liaison C-H n’a pas exactement la même constante de force que celle de la liaison C-D. Ces différences sont rassemblées sous l’expression «effet isotopique». Globalement, la vitesse de réaction mettant en jeu l’espèce isotopique la plus lourde est tout au plus de quelques pour cents plus petite que celle mettant en cause l’espèce isotopique la plus légère.
Des systèmes réactionnels ont été mis à profit pour enrichir et séparer une espèce isotopique particulière. C’est le cas de la préparation de l’azote 15 par échange isotopique entre le monoxyde d’azote NO, le dioxyde d’azote NO2 et l’acide nitrique sous pression.
| (15NO, 15NO2 ) gaz + H14NO3 liq | (14NO, 14NO2 ) gaz + H15NO3 liq |
Le procédé d’échange chimique a été étendu dans certains cas à la chromatographie échangeuse d’ions. Un récent procédé de préparation du lithium 7 fait appel à cette technique :
|
R- 7Li+ + 6Li+X- solution |
|
R- 6Li+ + 7Li+X- solution |
R- est un site échangeur de cations de la résine et X- un anion quelconque.
La spectrométrie de masse est l’outil idéal pour observer, mesurer certaines caractéristiques des isotopes. Chaque élément comporte un nombre connu d’isotopes en proportions très variables d’un élément à un autre. Certains ont des propriétés particulièrement intéressantes qui justifient des séparations industrielles quantitativement importantes comme cela est le cas pour l’industrie nucléaire (deutérium et uranium). D’autres servent de références analytiques en chimie alimentaire, en médecine, ...
|
| 6.1 | Au cours d’une réaction d’enrichissement isotopique à travers un système réactionnel mettant en jeu des atomes de chlore 35 et 37, on obtient du chlore moléculaire dont la masse molaire apparente est de 36,2 g. Calculez la proportion de chacun des deux isotopes dans le produit final. |
Réponse : 40 % de chlore-35 et de 60 % de chlore-37.
| 6.2 | Un élément est formé de deux isotopes A et B. La concentration de B dans A est de 0,025 %. On utilise un système de réactions chimiques qui produit un enrichissement de B de 1,7% à chaque étape. Établissez le nombre d’étapes nécessaires pour produire un mélange A et de B (90-10). |
Réponse : 451 étapes.
| 6.3 | Un minerai d’uranium naturel contient 0,75 % d’isotope 235 et le complément en isotope 238. Le procédé d’enrichissement isotopique utilise un système de diffusion gazeuse de l’hexafluorure d’uranium basé sur la loi de GRAHAM. Calculez le facteur d’enrichissement isotopique en admettant qu’il est égal au rapport des vitesses de diffusion. En déduire le nombre d’étages de diffusion nécessaires afin d’obtenir un hexafluorure contenant 10 % d’uranium 238. |
Lectures pour en savoir plus
Mark Pollard, A. et Carl. Heron, Archaeological Chemistry, The Royal Society of Chemistry, London, England, 1996.
Lambert, J. B., Traces of the Past - Unraveling the Secrets of Archaeology through Chemistry, Addison-Wesley, New York, Toronto, 1997.
Un numéro spécial de «L’Actualité chimique», août-septembre 2003, édité par la Société française de chimie, et intitulé «Les isotopes stables» contient plusieurs éléments intéressants relativement à l’analyse et aux usages des isotopes.
On trouvera
également dans la revue Elements, vol. 11, N° 4, année 2015, entre autres deux textes
sur l'usage de l'analyse isotopique:
1- J. R.
Ehlinger et al., Stable isotopes trace the truth: from adulterated food to crime
scenes, pages 259-264:
2- F. Albarède, Metal stable
isotopes in the human body: a tribute of geochemistry to medicine, pages 265-269.
Wikipedia demeure toujours une bonne source de références générales.
Des Prix Nobel :
J. J. THOMSON :
https://www.nobelprize.org/prizes/physics/1906/thomson/facts/ (visité le
2019-02-19)
UREY :https://www.nobelprize.org/prizes/chemistry/1934/urey/biographical/ (visité le 2019-02-19)
Dernière mise à jour: 2021-07-26.
XXXXXXXXXXXXXXX