CHAPITRE IV
ONDE ÉLECTROMAGNÉTIQUE - PHOTON
|
Pour compléter l’étude de l’électron, il est tout naturel de connaître les propriétés de l’assemblage des électrons dans un atome, autour d’un noyau. On sait, depuis l’expérience de RUTHERFORD, que cet assemblage ressemble au système solaire, les électrons faisant office de planètes tournant autour du noyau central. Questions :
|
1. Étendue du domaine des radiations électromagnétiques
Les échanges d’énergie entre l’atome (et la molécule) et le milieu extérieur, se font essentiellement par l’intermédiaire d’ondes électromagnétiques. Il est donc nécessaire d’étudier la nature et les propriétés de ces ondes. Des rayons g aux ondes de radio, on connaît tout un ensemble de phénomènes analogues aux phénomènes lumineux, dont la seule différence est la fréquence. Suivant le domaine d’étude des divers expérimentateurs, ces ondes ont été caractérisées, soit par la fréquence (inverse d’un temps), soit par la longueur d’onde (longueur), soit par le nombre d’onde (inverse d’une longueur).
On connaît la relation classique issue des phénomènes vibratoires mécaniques (cordes vibrantes par exemple) entre la longueur d’onde l, la vitesse de déplacement c de l’onde et la fréquence n :
l = c / n
Toutes les ondes électromagnétiques se propagent dans le vide (et en première approximation dans l’air) avec la même vitesse : la vitesse de la lumière c. En désignant par n la fréquence :
| 4.1 | l = c / n = c T |
Dans cette dernière
équation, T est la période. Les spectroscopistes de la
région visible et infrarouge caractérisent l’onde par le nombre d’onde que nous
désignerons conventionnellement par la lettre grecque "nu" srmontée d'une barre ![]() .
.
| 4.2 |
L’unité la plus couramment utilisée est le cm-1. Cette nouvelle notation a deux buts :
Nous verrons que la grandeur essentielle, celle qui a une signification physique, est la fréquence.
|
|
Figure 4.1. Caractéristiques du spectre électromagnétique.
La figure 4.1 donne la position des divers phénomènes dans ce qui constitue le spectre électromagnétique, ainsi que les unités utilisées dans les diverses régions.
2. Nature de l’onde électromagnétique
La théorie primitive de FRESNEL (1820) de la lumière visible considérait ce phénomène comme une onde mécanique.
Une onde mécanique est essentiellement le phénomène qui accompagne le déplacement d’une variation périodique sinusoïdale d’une grandeur qui caractérise le milieu. Cette grandeur est l’allongement d’un élément d’une corde vibrante, la variation de pression de l’air dans le cas du son ou la déformation d’un élément de volume, dans le cas des vibrations d’un solide. Cette théorie avait l’avantage d’expliquer complètement les phénomènes d’interférence déjà observés à propos des vibrations mécaniques. À l’époque, on ne savait rien de la grandeur physique variable, et FRESNEL la représenta par un vecteur vibrant.
La théorie électromagnétique de MAXWELL constitua un progrès important, puisqu’elle donna à ce vecteur vibrant une réalité physique. MAXWELL arriva à la conclusion que le vecteur vibrant était un vecteur champ électrique.
À ce vecteur champ électrique variable est associé un vecteur champ magnétique variable perpendiculaire. Cette théorie a le grand mérite d’interpréter les phénomènes de réflexion et de réfraction et de lier la constante diélectrique à la vitesse de l’onde dans le milieu. Les ondes radio ont apporté une brillante confirmation à cette théorie, puisque le champ électrique et le champ magnétique ont pu être directement mesurés (résonateurs de HERTZ). Des systèmes d’ondes stationnaires peuvent être également établis et l’intervalle entre les nœuds et les ventres mesurés avec précision. Enfin, la jonction entre les ondes hertziennes et les ondes de l’infrarouge lointain a été réalisée, c’est-à-dire qu’une radiation de même fréquence a été produite par des moyens électriques et par des phénomènes moléculaires. Les propriétés des ondes ainsi produites ont été expérimentalement reconnues identiques.
3. Condition nécessaire à l’émission d’onde électromagnétique
Notre ignorance des phénomènes élémentaires ne nous permet pas d’expliquer, mais seulement de constater que la variation périodique du moment dipolaire électrique d’un système est une condition nécessaire à l’émission d’onde électromagnétique.
Un exemple simple de cette condition est l’antenne de radio. L’oscillation applique à l’antenne un champ électrique alternatif. Ce champ a pour effet de séparer les charges positives et négatives du métal formant l’antenne qui prend ainsi un moment dipolaire. Ce moment dipolaire change de sens à la fréquence du champ. Une onde électromagnétique de même fréquence est rayonnée par l’antenne. L’amplitude de variation du moment dipolaire est en relation directe avec l’intensité de l’onde. Nous verrons que cette variation de moment dipolaire est fondamentale et s’étend également aux émetteurs atomiques et moléculaires.
Réciproquement, l’absorption de rayonnement électromagnétique crée une variation du moment dipolaire; c’est ce qui se passe dans l’antenne de réception. Mais ce moment dipolaire n’est induit que si la matière de l’antenne est polarisable. L’absorption de rayonnement par les atomes ou molécules crée également un moment dipolaire induit. Cette absorption est aussi liée à la polarisabilité de la matière.
4. Limitations à la théorie électromagnétique - la théorie quantique
NEWTON (1675) avait déjà postulé une théorie corpusculaire de la lumière, mais le succès de la théorie ondulatoire de FRESNEL avait relégué cette vieille idée au second plan. HERTZ lui-même, par une étrange coïncidence, devait découvrir l’effet :photoélectrique qui se révéla incompatible avec la théorie électromagnétique. À peu près à la même époque (1900), PLANCK introduisit également une théorie particulaire de l’énergie électromagnétique, pour expliquer les propriétés des radiations émises par le corps noir. Des confirmations supplémentaires sont ensuite venues de la photochimie et de l’effet COMPTON.
5. L'effet photoélectrique
HERTZ découvrit qu’une décharge électrique s’amorce plus facilement lorsque les électrodes sont exposées à la lumière ultraviolette. Cette constatation conduisit à étudier le comportement des métaux exposés à la lumière.
L’expérience fondamentale (Fig. 4.2) est faite dans une ampoule évacuée où se trouvent une plaque du métal à étudier et une plaque collectrice en regard. Les deux plaques étant reliées par l’intermédiaire d’un galvanomètre sensible, un courant est décelé lorsque le métal est illuminé. Le sens du courant indique que des particules chargées négativement s’échappent du métal. Les méthodes de déflexion électrique et magnétique combinées montrèrent que ces particules sont des électrons.
|
|
Figure 4.2. Dispositif expérimental pour étudier l’effet photoélectrique.
Une différence de potentiel introduite dans le circuit, s’oppose ou favorise le passage des électrons selon son signe. L’étude du courant photoélectrique montre que l’on peut s’opposer complètement au passage des électrons par un potentiel convenable ou potentiel d’arrêt Va. La loi de conservation de l’énergie, montre que ce potentiel est en relation avec l’énergie cinétique maximale Em des électrons.
Em = 1/2 m u2 = e Va
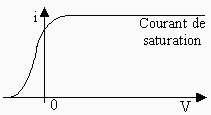 Courant i = f(tension). |
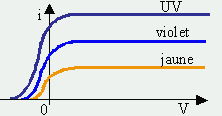 Effet de la longueur d’onde. |
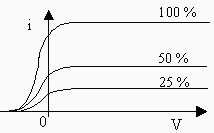 Effet de l’intensité lumineuse. |
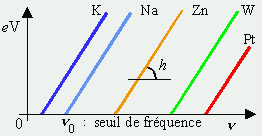 Effet de la tension d’accélération. |
Figures 4.3. Effet photoélectrique.
Note : L’intensité du courant
photoélectrique n’est pas liée à la longueur d’onde de la lumière incidente.
On peut donc déduire E de la mesure de V. Si on illumine un même métal avec des fréquences différentes, on constate la relation expérimentale :
|
4.3 |
Em = hn - E0 Þ Em - E0 = hn |
L’équation 4.3 traduit simplement le principe de la conservation de l’énergie suivant :
énergie cinétique de l’électron = énergie d’un quantum de lumière - énergie nécessaire à l’extraction de l’électron |
Si on utilise des métaux différents, h ne varie pas mais E0 dépend du métal. L’intensité de la lumière est sans aucune influence sur la valeur de Em. EINSTEIN donna la théorie de ce phénomène. La lumière apparaît comme formée de particules transportant l’énergie hn. S’il en est ainsi, on ne doit plus observer d’effet photoélectrique si on diminue n de telle manière que :
hn < E0 .
Cette conséquence est expérimentalement observée et définit le seuil photoélectrique du métal:
|
4.4 |
n 0 = E0 / h |
La constante h avait déjà été introduite à l’époque par la théorie de PLANCK du rayonnement du corps noir.
Tableau 4.1.
Travail de sortie d'un électron d'une plaque métallique
|
Métal |
Cs |
K |
Mg |
Zn |
Fe |
Ni |
|
Potentiel
de sortie en volts |
2,1 |
2,4 |
2,4 |
3,4 |
4,8 |
5,0 |
6. Le rayonnement du corps noir
Ce rayonnement, analysé au spectrographe, couvre un large domaine de fréquences. À chaque température, la répartition de l’énergie émise par le corps noir en fonction de la fréquence n’est pas la même. Le maximum d’émission se déplace vers les grandes fréquences, lorsque la température croît. De plus, les faibles fréquences sont beaucoup mieux représentées dans le spectre que les grandes fréquences (Fig. 4.4).
Bien que les détails de la théorie ne puissent être présentés de façon simple, il est important d’en connaître les principes. Considérons un corps noir en équilibre thermique (Fig. 4.4A). Il est constitué par un grand nombre de molécules ou atomes qui sont mis en vibration par l’énergie thermique fournie par le milieu extérieur. Ces atomes ou molécules émettent de l’énergie électromagnétique dans tout le domaine spectral par leurs mouvements de vibration (Fig. 4.4B). Ces vibrations de masses chargées, entraînent des variations locales de moment dipolaire et chaque molécule se comporte comme un poste émetteur. Ce raisonnement est la stricte conséquence de la théorie électromagnétique. On peut ensuite traduire le fait que l’équilibre thermique est atteint en appliquant le principe d’équipartition de l’énergie qui déclare que dans ces conditions, l’énergie moyenne de vibration de chaque molécule est la même (égale à R T / N = kT). La fréquence de vibration des atomes peut varier dans un domaine très large (Fig. 4.4C).
A 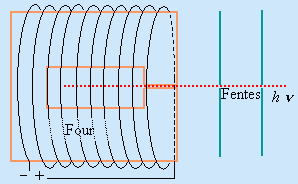 |
Four
B |
réseau cristallin
|
C |
Figures 4.4. Rayonnement du corps noir.
Il est possible de calculer ensuite la répartition de l’énergie émise en fonction de la fréquence. On trouve que l’intensité de radiation devrait décroître avec l’augmentation de la fréquence (nombre d’oscillateurs est proportionnel à l-4 dans un intervalle dl), ce qui est observé dans la région des courtes longueurs d’onde (grandes fréquences). Cependant, ce résultat est en contradiction formelle avec l’expérience, puisque du côté de l’infrarouge, le rayonnement du corps noir tend rapidement vers zéro.
Dans le but d’éviter ce désaccord, PLANCK (1900) observa que le principe d’équipartition de l’énergie appliqué aux molécules vibrantes, devait avoir certaines limites. Il postula qu’une molécule vibrant à sa fréquence caractéristique n peut emmagasiner l’énergie sous forme de paquets. Ces paquets, ou quanta, seraient des multiples entiers d’un paquet élémentaire hn ( 0, hn, 2 hn, 3 hn, 4 hn, . . ). La constante h serait une constante universelle valable pour une particule vibrante quelconque. En d’autres termes, cette hypothèse affirme que l’énergie d’une molécule ou atome a une structure quantifiée.
Avec cette hypothèse, la courbe expérimentale peut être interprétée. Les molécules vibrent sous l’action de collisions thermiques mettant en jeu des énergies dont la valeur n’est pas très élevée. Celles dont la fréquence propre est faible, vont pouvoir vibrer puisque le quantum hn est petit. Elles le feront non seulement avec une énergie d’un quantum, mais aussi avec une énergie équivalente à 2, 3, 4,... n quanta, en autant que la valeur nhn soit compatible avec l’énergie disponible kT. Celles dont la fréquence propre n est grande ne vibreront pas car l’énergie thermique sera impuissante à fournir le quantum hn minimum qui leur est nécessaire pour vibrer. Ce fait explique la décroissante rapide du rayonnement pour les fréquences élevées (basses longueurs d’onde). En intégrant :
![]()
Dans cette équation I est l’énergie émise dans une région dl du spectre électromagnétique. On montre que l’énergie totale émise par le corps noir est donnée par la relation suivante :
W = 5,6705 10-8 T4 W · m-2
(loi de STEPHAN-BOLTZMANN). On peut aussi montrer que le maximum est donné par la loi de WIEN :
![]()
Dans cette formule :
h est la constante de Planck
k est la constante de Boltzmann et
c la vitesse de la lumière.
L’hypothèse de PLANCK concerne seulement le contenu énergétique des particules. Elle ne prévoit pas que ce contenu, une fois libéré, traverse l’espace sous forme de l’entité hn. Mais la théorie de PLANCK a introduit pour la première fois le concept nouveau de la théorie quantique des atomes et molécules.
7. Réactions photochimiques
EINSTEIN a proposé la loi fondamentale de la photochimie, en même temps que l’équation de l’effet photoélectrique. En photochimie (étude des réactions induites par la lumière) la réaction se produit en plusieurs étapes successives. L’absorption de lumière provoque d’abord une réaction primaire qui est suivie par les réactions secondaires des atomes ou des radicaux libres produits.
EINSTEIN affirma:
"Chaque quantum de lumière absorbée provoque la réaction primaire dans une molécule".
Cette théorie donne du même coup, l’explication d’un fait connu depuis longtemps : la lumière ultraviolette est beaucoup plus efficace que la lumière visible dans l’initiation des réactions photochimiques. Le changement chimique qui s’opère dans la molécule nécessite un minimum d’énergie qui doit être apportée par le photon. Ce minimum ne sera atteint, c’est-à-dire la réaction n’aura lieu, que si la fréquence a une valeur convenable, de préférence élevée.
La sensation rétinienne semble être reliée à une réaction photochimique, de même que la photosynthèse qui permet aux plantes de construire des chaînes carbonées à partir du CO2 atmosphérique. Un exemple chimique classique est celui de la photodissociation de HI suivant le schéma :
HI + hn ® H + I·
H + HI ® H2 + I·
I· + I· ® I2.
Il faut bien sûr que hn soit au moins égal à l’énergie de dissociation de HI. On observe expérimentalement la production d’une molécule d’hydrogène et d’une molécule d’iode pour chaque photon absorbé.
Les rayons X sont de même nature électromagnétique que la lumière visible. On peut les faire interférer ou diffracter (par exemple par les cristaux). Cependant un phénomène n’est explicable que si l’on fait intervenir l’hypothèse quantique : c’est l’effet COMPTON (Fig. 4.5 et 4.6).
Des rayons X de fréquence soigneusement définie, tombant sur un matériau de poids atomique faible comme le carbone ou la paraffine, présentent un changement de fréquence. Bien que le faisceau diffracté contienne toujours du rayonnement ayant la fréquence initiale, un rayonnement de fréquence plus faible est observé, la différence de fréquences dépendant de l’angle que font le faisceau incident et le faisceau diffracté. La théorie de l’effet COMPTON considère le quantum de lumière X comme une particule qui perd son énergie par collision avec un électron. Le problème est traité par la mécanique classique comme celui d’une collision entre deux boules de billard. Le principe de conservation de la quantité de mouvement et le principe de conservation de l’énergie sont successivement appliqués (figure 4.6).
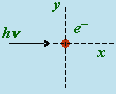 |
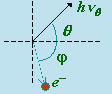 |
| avant | après |
Figure 4.5. Collision entre un photon et une particule (électron).
|
|
Figure 4.6. Effet COMPTON : combinaison vectorielle des quantités de mouvement.
Tableau 4.2. Effet COMPTON : bilans
| Particule | Énergie | Quantité de mouvement |
| photon incident | hno | hno / c |
| photon diffusé | hnq | hnq / c |
| électron au repos | moc2 | 0 |
| électron de recula |
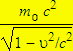 |
|
a) En relativité: changement de vitesse + changement de masse. |
||
L’équation traduisant la conservation de l’énergie est :
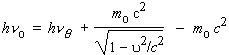
L’équation traduisant la conservation de la quantité de mouvement est (quantités vectorielles):
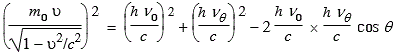
La résolution de ce système de deux équations à deux inconnues (u et q) donne la grandeur que l’on peut mesurer expérimentalement (nq ). Il faut prendre la vitesse relativiste de l’électron car il a une grande vitesse.
| 4.5 | 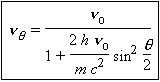 |
La mesure de nq en fonction de l’angle q donne effectivement des résultats concordants avec cette théorie. Une autre façon de présenter le calcul est de calculer la différence de longueur d’onde entre le photon diffracté et le photon incident :
![]() .
.
9. La collision dans un système classique
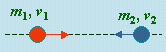
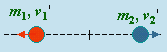
Dans un système où l’on considère la collision de deux particules, m1 et m2, animées chacune de leur vitesse, v1 et v2, on est évidemment intéressé à connaître ce qui se passe après collision. Dans un premier temps admettons que les deux masses ne sont pas ponctuelles, mais occupent une portion sphérique de l’espace si faible soit elle, un peu comme des billes ou des boules sur un jeu de billard. Par souci de simplicité, les masses se déplacent dans le même plan et que leur trajectoire les amèneront à entrer en collision. Premier cas de figure, les trajectoires sont colinéaires : les deux masses m1 et m2 ont une vitesse v1 et v2, (v2 étant négative par rapport à v1 qui, elle, est positive) (Fig. 4.7).
 |
 |
|
| avant collision | après collision |
Figure 4.7. Une collision colinéaire.
Dans ce cas on exprime les règles de conservation de la quantité de mouvement ainsi que celle de l’énergie cinétique. Par ailleurs, supposons qu’il n’y a aucune force extérieure agissant sur le système et que la collision est élastique. On écrit alors :
| 4.6 |
m1 v1 + m2 v2 = m1 v1' + m2 v2' |
|
et |
|
| 4.7 |
1/2 m1 v12 + 1/2 m1 v12 = 1/2 m1 v1'2 + 1/2 m1 v1'2 |
Voilà deux équations à deux inconnues, v1' et v2' , les vitesses des deux masses après collision. Évidemment avec le système matériel décrit (deux trajectoire colinéaires, des boules ou billes sphériques) après collision, les deux masses demeurent sur le même axe. Il n’y a donc pas changement de trajectoire. Les deux équations permettent de préciser, calculer ces deux inconnues.
 |
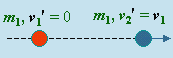 |
|
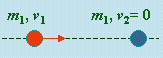
| avant collision | après collision |
Figure 4.8. Le "carreau" au jeu de pétanque.
Un premier cas d’espèce est celui où les deux masses sont identiques, m1 = m2, et où la deuxième masse, par exemple, est sans mouvement avant la collision (Fig. 4.8). Les deux équations deviennent :
| 4.6 devient | m1 v1 = m1 v1' + m2 v2' |
|
Þ |
v1 = v1' + v2' |
| 4.7 devient | 1/2 m1 v12 = 1/2 m1 v1'2 + 1/2 m1 v1'2 |
|
Þ |
v12 = v1'2 + v1'2 |
| 4.8 | v1' = v1 - v2' et v1'2 = v12 - 2 v1 v2' + v1'2 |
|
4.9 Þ |
v12 - v1'2 = v2'2 = v12 - v12 + 2 v1 v2' - v2'2 |
| 2 v2'2 = 2 v1 v2' | |
|
Þ |
v2' = v1 |
| v1' = 0 |
Tout se passe comme si la masse m1 transfère intégralement son énergie cinétique à la masse m2. Cette dernière part après collision avec la vitesse v1 alors que la première masse s’arrête. C’est ce que les joueurs de pétanque appellent "faire un carreau".
Un deuxième cas d’espèce est celui où les deux masses identiques sont animées d’une même vitesse absolue mais de signe opposés. La résolution des deux équations précédentes montrent, qu’après collision, les deux masses repartent sans échange d’énergie cinétique mais en inversant leur signe de vitesse : elles échangent leur quantité de mouvement.
Un cas de figure plus difficile à résoudre est celui de deux masses quelconque animées de vitesse différentes sur deux axes coplanaires mais non colinéaires. Supposons qu’il y ait toujours collision élastique. La trajectoire initiale de la masse m2 se situe à un angle q par rapport à la direction de progression de la masse m1. Plaçons le centre de coordonnées cartésiennes au centre de collision. La quantité de mouvement étant une grandeur vectorielle, on peut décomposer la quantité de mouvement par rapport à chacun des axes Ox et Oy. Ainsi la précédente équation 4.6 se décompose en équations (4.6') et (4.6") :
| 4.6' |
m1 v1,x + m2 v2,x = m1 v1,x' + m2 v2,x' |
|
et |
|
| 4.6'' |
m1 v1,y + m2 v2,y = m1 v1,y' + m2 v2,y' |
Si m1 se meut initialement sur l’axe Ox, la quantité m1v1,y = 0. Par ailleurs, la quantité d’énergie cinétique n’étant pas une grandeur vectorielle, l’équation 4.7 ne peut se décomposer sur chacun des deux axes de référence. On dispose donc de 3 équations pour obtenir 4 inconnues, ces dernières étant v1', v2' et leur direction ou encore v1,x', v1,y', v2,x' et v2,y'.
Le système est indéterminé et la figure de
sortie des deux billes après collision est quelconque. On
verra quelques lignes plus bas que cette décomposition des vecteurs vitesse sur
les deux axes ne constitue pas une bonne approche.
Demeurons un instant encore avec le cas des deux boules sphériques de volume fini (et non de deux masses ponctuelles), il tombe sous le sens que la figure de sortie après collision est influencée, déterminée par les tangentes au point de contact sur collision des deux boules. Les joueurs de billard en savent quelque chose. Dans ce cas les centres de deux boules ne se percutent pas sur le point de concours des deux trajectoires initiales (boules de rayon infiniment petit).
Le centre de masse
Précisons maintenant que les deux masses m1 et m2 sont ponctuelles (donc en quelque sorte immatérielles): elles n’occupent aucun volume. Elles sont en mouvement sur deux axes différents, coplanaires et il y a collision en un point O. Définissons le centre de masse G, aussi et à l’occasion maladroitement appelé centre de masse. À un instant donné, avant collision, la position du centre de masse sera déterminé par la relation (applicable à n corps faisant partie du système considéré) :
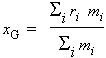
Dans cette équation, ri est la distance de la particule de masse mi au centre de masse. En fait cette relation est vraie quel que soit le nombre de particules considérées. Pour un système ne mettant en jeu que deux particules,
![]()
Regardons de plus près la dérivée de la position du centre de masse par rapport au temps (le système de i particules est en mouvement):
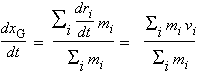
La valeur de Si mi vi n’est rien d’autre que la quantité de mouvement totale du système. Si aucune force extérieure n’agit sur le système de i particules, cette somme reste constante. Donc dxG/dt est aussi une constante. La vitesse du centre de masse n’est aucunement affectée par la collision. Comme la démonstration peut se faire quelle que soit l’orientation de chacun des déplacements (la vitesse et la quantité de mouvement étant des grandeurs vectorielles), en l’absence de force externe, le déplacement du centre de masse est inchangé par la collision.
|
|
Figure 4.9. Collision de deux masses ponctuelles, immatérielles
Revenons au cas d’espèce de deux masses ponctuelles se déplaçant de manière colinéaire, l’une vers l’autre, avec les vitesses v1 et -v-1. La condition se limite à laisser la position du centre de masse inchangé par la collision. Cette fois la solution de sortie est multiple : les particules doivent se séparer de manière opposée, sur le même axe, sans autre définition de l’orientation de cet axe... Rappelons ici que le couplage qui s’exercerait sur les boules au point d’impact n’existe plus. En fait quelles que soient les directions des deux axes de propagation avant collision, il existe une infinité de solutions, la seule condition est que la propagation du centre de masse demeure inchangée.
|
|
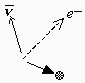 |
| avant émission | après émission |
Figure 4.10. Émission du rayonnement b-.
Un autre cas d’application intéressant est celui de la désintégration radioactive d’un noyau. Par exemple, dans le cas de l’émission d’un rayonnement b-, il y a simultanément émission d’un antineutrino. Là encore, le centre de masse du système (le noyau avant désintégration) poursuit sa trajectoire sans modification (absence de force extérieure) (Fig. 4.10). Après désintégration, la direction de chacune des particules émises est quelconque. Par contre, le centre de masse de ces particules continue sur sa lancée. En fait, la distribution des forces nucléaires au moment de la désintégration a probablement beaucoup à voir sur les trajectoires des éléments de fission: cela est une autre histoire. Bien évidemment, on trouve la même infinité de solutions dans le cas de deux particules ponctuelles, de masse quelconque, qui entrent en collision sur deux trajectoires situées à un angle q l’une par rapport à l’autre.
Autre cas de figure : celui où le système de particules est soumis à une force extérieure. C’est le cas, par exemple, d’un proton projeté vers un noyau (force répulsive de nature électrostatique) ou d’un satellite ou d’une comète qui s’approche d’un astéroïde, d’une planète ou d’un autre corps céleste (force attractive de nature gravitationnelle). Dans ces cas, la quantité de mouvement varie au cours de la collision et dxG/dt n’est plus une constante.
10. Conclusion - La mécanique ondulatoire
Toutes ces évidences en faveur de la théorie quantique ne signifient pas que l’on doive rejeter la théorie électromagnétique, pas plus qu’il ne faut considérer une particule quelconque comme une onde. Aucune de ces deux alternatives ne représente la vérité absolue. Le désir de concilier les deux théories en une théorie mathématique unique a fait naître la mécanique ondulatoire.
Dans cette mécanique, on suppose que les ondes qui se propagent ne transportent pas de l’énergie uniformément répartie sur tout le front d’onde, comme dans le cas des ondes à la surface de l’eau ou des ondes sonores. Au contraire, l’énergie est concentrée en quanta d’énergie hn. Les ondes, ont simplement pour fonction, de décrire la probabilité qu’ont les quanta de se trouver en un point particulier.
La mécanique ondulatoire utilise au départ la mécanique des ondes matérielles sinusoïdales classiques. On démontre que, quel que soit le système mécanique considéré (corde vibrante, son, déformations élastiques des membranes ou des solides), la déformation du milieu U qui est une fonction sinusoïdale du temps satisfait à l’équation différentielle suivante appelée équation générale de propagation des ondes planes.
| 4.10 | 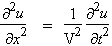 |
x est la coordonnée de position (Ox est la direction de propagation); t le temps; u la vitesse de propagation. MAXWELL a montré que cette équation s’étendait également à la propagation du champ électrique de l’onde électromagnétique. Il est aisé de vérifier que la solution générale de l’équation 4.6 est :
| 4.11 | U = f ( V t - x ) + g ( V t + x ) |
f et g étant deux fonctions dont la forme dépend des conditions aux limites. Prenons l’exemple d’un ébranlement sinusoïdal appliqué à l’origine d’une corde tendue :
![]()
On sait que, en un point x de la corde, on a superposition de deux mouvements :
| l’onde incidente : l’onde réfléchie : |
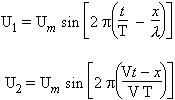 |
le mouvement résultant est bien: U = U1 + U2 qui a la forme 4.7.
Dans le cas d’une onde plane ne se propageant par en ligne droite, l’équation 4.10 généralisée donne :
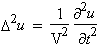
Dans cette équation, D2U est le Laplacien de la fonction u, et x, y, z sont les coordonnées d’un point de l’espace, c’est-à-dire :
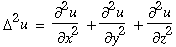
ÉQUATION DE SCHRÖDINGER - Application de la mécanique des ondes matérielles au mouvement des particules.
Cette équation, base de la mécanique quantique des atomes et molécules, résulte de l’application de l’équation générale de propagation des ondes planes au mouvement de l’onde associée à une particule.
Deux hypothèses sont cependant nécessaires à priori. Elles seront vérifiées par la validité des résultats des calculs de mécanique ondulatoire :
a) les ondes de DE BROGLIE sont des ondes planes
b) la perturbation est une fonction sinusoïdale du temps.
Cette dernière hypothèse est très audacieuse puisque en fait, nous ne savons rien sur la nature physique de la perturbation. Nous pouvons seulement introduire une fonction d’onde qui sera l’homologue de la déformation de la corde vibrante ou du champ électrique de la théorie de MAXWELL. Cette fonction des coordonnées doit être sinusoïdale par rapport au temps. Elle peut se décomposer de la manière suivante :
j (x, y, z, t) = y (x, y, z) sin (2 pn t)
La fonction y (x, y, z) est une fonction d’amplitude. Dans ces conditions, l’équation aux dérivés partielle devient en identifiant u et j(x) (problème à une dimension seulement) :
| 4.12 |
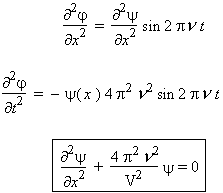 |
C’est l’équation d’onde dans laquelle la variable temps est supprimée. Dans le cas d’un problème à trois dimensions, elle s’écrit :
| 4.13 | Dans cette équation D2u est le laplacien. |
Cette équation donne la valeur de la fonction d’amplitude y en chaque point de l’espace. Pour appliquer cette relation, au cas de l’onde associée à une particule, on fait intervenir la relation de DE BROGLIE de la manière suivante : l’énergie totale E de la particule est la somme de son énergie cinétique mu2 et de son énergie potentielle U :
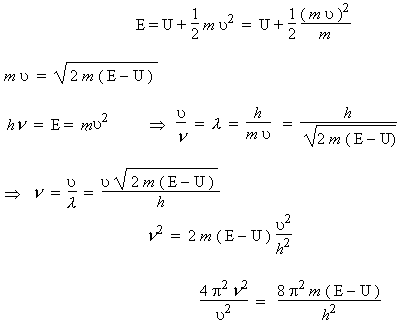
Ce qui conduit à l’équation dite équation de SCHRÖDINGER (en remplaçant la valeur de n2 dans l'équation 4.13) :
| 4.14 | 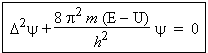 |
Cette équation permet de déterminer E et y lorsqu’on connaît le potentiel U dans lequel se déplace la particule. Elle a pris une importance si grande dans la mécanique de l’atome qu’on traite comme l’équation fondamentale de la mécanique ondulatoire, de même que F = m g est l’équation fondamentale de la mécanique classique.
L'effet photoélectrique et l'effet COMPTON sont entièrement explicables sur la base de la mécanique classique. Par ailleurs l'explication du comportement du corps noir réclame une approche quantique. C'est l'intérêt de la mécanique ondulatoire de pouvoir intégrer ces deux approches et de les unifier. L'équation de SCHROEDINGER permettra éventuellement d'expliquer quantitativement l'ensemble de ces phénomènes.
|
Liens intéressants :
En provenance de l’Université du Tennessee, un site Web consacré à l’Astronomie présente plusieurs éléments intéressants (y inclus une bibliographie de sites web). On y trouvera une présentation du modèle de BOHR, ainsi que la description des séries de BALMER
Modèle de BOHR :
http://csep10.phys.utk.edu/astr162/lect/light/bohr.html
(visité le 2015-01-11)
Série de BALMER, ... :
http://csep10.phys.utk.edu/astr162/lect/light/absorption.html
(idem).
Par ailleurs, le site web de la Georgia State University présente des "diapos" très intéressantes relativement à l’effet COMPTON, à l’effet photoélectrique,... et à beaucoup d’autres choses. Ce site, qui peut aussi être avantageusement utilisé comme glossaire à travers son index, a été construit par Carl R. (Rod) Nave :
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Note : on se servira de l’index pour trouver les éléments rechercher : Compton scaterring, Compton wavelength, Photoelectric effect, Blackbody radiation, ...
Et encore des biographies, site visité le 2015-01-15, dont celles de Whilhelm WIEN, Erwin SCHRÖDINGER, Max PLANCK, Sir Isaac NEWTON et Augustin FRESNEL ainsi que beaucoup d'autres.
COMPTON :
http://nobelprizes.com/nobel/physics/1927a.html
SCHRÖDINGER :
http://nobelprizes.com/nobel/physics/1933a.html
MAXWELL http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Maxwell.html
Une nouveauté: Les constantes de PLANCK et de BOLTZMANN remesurées: J. Kensley, Chem. & Engin. News, page 10 (July 2018); Documents originaux:
http://iopscience.iop.org/article/10.1088/1681-7575/aa7bf2/meta et http://iopscience.iop.org/article/10.1088/1681-7575/aa7b3f
11. Problèmes
| 11.1 | Quelle est l’énergie en cm-1, en joules, des photons émis par la lampe à mercure : l = 253,7 nm ? |
Réponse : E = 7,829 10-19 J.
| 11.2 | En étudiant la photoémission d’électrons à partir du calcium, on trouve les tensions retardatrices, Vo, maximum suivantes : |
| l (nm) | 253,6 | 313,2 | 365,0 | 404,7 |
| Vo (volts) | 1,95 | 0,98 | 0,50 | 0,14 |
Représenter graphiquement ces résultats et en déduire la valeur du travail de sortie, Eo, et celle de la constante de PLANCK.
Rép. Eo = 2,865 volts.
| 11.3 | En étudiant l’effet photoélectrique sur différents métaux, on détermine les longueurs d’onde maximum à partir desquelles aucun courant n’est visible. Ainsi, pour ces métaux, les seuils photoélectriques sont les suivants : Li : 537 nm, Na : 647 nm, K : 700 nm et Cs : 750 nm. Calculez, en eV, l’énergie minimum d’extraction des électrons pour chacun de ces métaux. |
Réponse : Eo(K) = 1,77 eV.
| 11.4 | Le maximum lmax pour le rayonnement solaire se produit à une longueur d’onde voisine de 480 nm. En supposant que le Soleil se comporte comme un corps noir, estimer sa température superficielle. |
Réponse : T = 6 035 K.
| 11.5 | Deux véhicules ponctuels de même masse, M1 = M2, sont situés sur le même axe Ox. Le premier véhicule se déplace avec une vitesse v1 et se dirige vers le second qui est au repos. Calculez la vitesse des deux véhicules après collision, collision que l’on considérera élastique. |
Réponse : Le véhicule 1 transfère toute son énergie au véhicule 2 et prend sa place. Le véhicule 2 s’en éloigne avec une vitesse v1. Au jeu de pétanque, cette transformation s’appelle "faire un carreau".
| 11.6 | Deux véhicules ponctuels, de même masse, M1 = M2, sont situés sur le même axe Ox et se dirigent l’un vers l’autre, le premier avec une vitesse égale à 2 v1, le second avec une vitesse -v1. Calculez la vitesse des deux véhicules après collision, collision que l’on considérera élastique. |
| 11.7 | Un faisceau de rayons X ( l = 0,055 8 nm) est dévié de 45°. Trouver la longueur d’onde des rayons X déviés. |
Réponse : l = 0,0565 nm.
| 11.8 | Le travail de sortie (extraction d’un électron) du tantale est de 4,19 eV. En éclairant une plaque de ce métal avec la raie de résonance du mercure ( l = 253,7 nm), quelle est l’énergie cinétique maximum des électrons extraits en eV ? |
Réponse : Ec = 0,695 volts ou 67,1 kJ / mol.
| 11.9 | Le filament en tungstène d’une lampe fonctionne normalement à 2900 K. En supposant que ce filament fonctionne selon la définition du corps noir, quelle sera la longueur d’onde du maximum du spectre d’émission ? |
Réponse : lmax = 999 nm.
| 11.10 | L’œil humain a une sensibilité maximum située à une longueur d’onde de 550 nm. Quelle est la température optimum d’une ampoule électrique utilisée comme source de lumière ? |
Dernière mise à jour : 2021-07-23.
____________________________