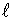 et m. Le tableau suivant résume ces trois nombres et les grandeurs qui
sont quantifiées : n quantifie l’énergie et
et m. Le tableau suivant résume ces trois nombres et les grandeurs qui
sont quantifiées : n quantifie l’énergie et 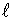 quantifie le moment angulaire orbital. Le
nombre m fixe la projection du moment cinétique sur l’axe Oz par la relation :
quantifie le moment angulaire orbital. Le
nombre m fixe la projection du moment cinétique sur l’axe Oz par la relation :INFLUENCE D'UN CHAMP MAGNÉTIQUE SUR LES NIVEAUX D'ÉNERGIE
QUANTIFICATION SPATIALE
|
On a vu que pour chacun des atomes le moment magnétique de spin vient s’ajouter au moment orbital. Si l’on immerge un atome dans un champ magnétique intense, comment interagit ce champ magnétique avec le moment magnétique de l’atome ? Ce dernier s’oriente-t-il dans le sens du champ uniquement comme le fait l’aiguille d’une boussole dans le champ magnétique terrestre ? Questions : Objectifs :
|
Nous avons vu que, dans le cas des atomes
hydrogénoïdes, la solution de l’équation de SCHRÖDINGER introduit trois nombres
quantiques n, 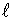 et m. Le tableau suivant résume ces trois nombres et les grandeurs qui
sont quantifiées : n quantifie l’énergie et
et m. Le tableau suivant résume ces trois nombres et les grandeurs qui
sont quantifiées : n quantifie l’énergie et 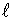 quantifie le moment angulaire orbital. Le
nombre m fixe la projection du moment cinétique sur l’axe Oz par la relation :
quantifie le moment angulaire orbital. Le
nombre m fixe la projection du moment cinétique sur l’axe Oz par la relation :
Pz = m h / ( 2 p ) = m h
Tableau 9.1. Nombres quantiques principaux
| Nombre | Rappel | Grandeur quantifiée (formule) : |
n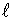 m |
entier, positif, n - 1 ≥ 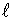 ≥
0
≥
0- 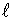 ≤
m ≤
+
≤
m ≤
+ 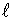 |
Énergie : En
- EI/n2
= 2 n2 m e4 Z2 / (h n)2 |
En l’absence de toute intervention extérieure, les niveaux d’énergie correspondant aux valeurs possibles de m sont dégénérés, c’est-à-dire qu’ils possèdent la même énergie. Nous allons voir qu’il n’en est plus de même lorsque l’atome est placé dans un champ magnétique par suite de l’interaction entre le champ extérieur et les champs internes créés par le mouvement orbital et le spin.
2. Moment magnétique associé au moment orbital
Soit un électron tournant autour du noyau sur une orbite sous l’action de la force centrale de COULOMB. Puisque la force est centrale, le moment cinétique P est constant et on a par définition :
![]()
En valeur absolue, ce vecteur est égal à l’aire du parallélogramme construit sur les vecteurs meu et r (Fig. 9.1).
|
|
Figures 9.1.
Pendant le temps dt, l’électron se déplace de M en M' et MM' peut être considéré comme un vecteur de longueur udt. L’aire dS balayée par le rayon vecteur pendant le temps dt est égale à la moitié de l’aire du parallélogramme construit sur les vecteurs r et u dt. Ce parallélogramme et le parallélogramme précédent ont leurs côtés parallèles et ils ont de plus un côté commun. Leurs aires sont donc dans le rapport des deux autres côtés.
L / 2 dS = me u / u dt
9.1 dS / dt = L / 2 me dS / dt = L / 2 me
dS/dt est la vitesse aréolaire (vitesse avec laquelle le rayon vecteur balaie l’ellipse) et l’équation précédente exprime que la trajectoire est parcourue suivant la loi des aires, propriété générale à tous les moments à force centrale. On peut maintenant trouver une relation entre la vitesse aréolaire et le moment magnétique.
L’électron tournant sur son orbite est l’équivalent
d’un courant électrique dans une spire. On sait qu’un tel courant produit un champ
magnétique à l’intérieur de la spire, donc que le système est identique à un petit
barreau aimanté. Un tel barreau de longueur l
possédant les deux masses magnétiques +m
et -m aurait un moment magnétique égal à m
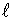 . On
montre que la spire a un moment magnétique :
. On
montre que la spire a un moment magnétique :
M = I S
I étant l’intensité du courant et S la surface de la spire. L’électron de charge -e qui fait n tours par seconde est équivalent à un courant I = - n e donc à un moment :
M = - n e S
La vitesse aréolaire, ds/dt, est l’aire balayée par le rayon vecteur par seconde, soit :
ds/dt = n S
| D’où :
|
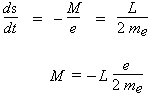 |
À un moment cinétique p de l’électron est associé un moment magnétique dont la valeur est donnée par 9.2. Le raisonnement précédent montre également que M est un vecteur colinéaire au vecteur L mais de sens opposé.
3. Magnéton de BOHR
Il est commode de choisir une unité de moment magnétique à l’échelle atomique, l’unité électromagnétique étant d’un ordre de grandeur beaucoup trop grand. Cette unité avait d’ailleurs été suggérée à BOHR par des considérations expérimentales sur la susceptibilité magnétique (voir plus loin, Chapitre X). Il apparaît tout naturellement, d’après la théorie quantique une unité de moment cinétique: c’est la quantité h/(2 p). Nous avons vu que les moments cinétiques atomiques prennent des valeurs multiples entier (ou demi entier) de cette quantité. On peut associer à cette unité de moment cinétique une unité de moment magnétique appelée magnéton de BOHR dont la valeur absolue est (en SI) :
| 9.3 |
où µB = 0,927 3 ´ 10-23 J/(Wb/m2)
Suivant la valeur du nombre quantique orbital: 0, 1, 2, 3, etc., le moment magnétique associé au mouvement orbital d’un électron sera :
0, µB , 2 µB , 3 µB, etc.
Cette notion se généralise au moment orbital total L par addition vectorielle. L’atome possède le moment magnétique orbital - L µB. On sait que la valeur exacte du moment cinétique est
![]() ´
h/(2 p).
´
h/(2 p).
La valeur exacte du moment magnétique associé est donc :
ML =
- ![]() µB
µB
4. Moment magnétique associé au spin de l’électron
On peut imaginer qu’un moment magnétique est associé à la rotation de l’électron sur lui-même en assimilant ce dernier à une sphère chargée tournant autour d’un de ses diamètres. Cette rotation entraîne un mouvement des charges produisant un moment magnétique colinéaire et opposé au moment cinétique. Il serait absurde d’essayer de calculer le moment magnétique en supposant une certaine distribution de charges sur une sphère puisqu’on ne connaît rien de la nature de l’électron. Aussi étrange que cela puisse paraître, le moment magnétique associé au spin peut être mesuré directement (voir paragraphe suivant).
Au moment cinétique (1/2) (h/2 p) est associé 1 magnéton de BOHR.
Ce résultat n’est qu’en contradiction apparente avec le
résultat précédent, spin et mouvement orbital étant le mouvement de nature
différente. Il en résulte qu’à un spin total S h/(2 p)
correspond le moment magnétique 2 S µB. La valeur exacte du
spin total étant ![]() ´ h/(2
p), la valeur exacte du moment magnétique associé est donc :
´ h/(2
p), la valeur exacte du moment magnétique associé est donc :
![]()
5. Mise en évidence et mesure directe des moments magnétiques atomiques - Expérience de STERN et GERLACH - Quantification spatiale
L’expérience de STERN et GERLACH est fondamentale pour la théorie atomique. Elle permet de mesurer les moments magnétiques atomiques et de mettre en évidence le phénomène de quantification spatiale. Si on place un petit aimant dans le champ magnétique H (direction Oz), on sait que cet aimant va tendre à s’orienter dans le sens du champ si le champ est uniforme car, dans ce cas, l’aimant est soumis à un couple. Si le champ n’est pas uniforme, il s’orientera et se déplacera latéralement sous l’action d’une force Fz. L’énergie de l’aimant dans le champ magnétique est donnée par l’expression générale (q étant l’angle de que font les vecteurs M et H ) :
|
|
Figure 9.2.
W = -
M ![]() =
- M H cos q
=
- M H cos q
9.4 Fz = - dW/dz = - M dH/dz cos q
L’atome possédant le moment magnétique M aura le même comportement. Il va s’orienter (pas nécessairement dans le sens du champ comme nous le verrons plus loin) et se déplacer latéralement. Si on veut observer cette orientation et ce déplacement, il faut faire passer un jet d’atomes dans un champ non uniforme, dont le gradient varie le plus rapidement possible dans une direction. On y parvient en produisant un jet atomique dans le vide entre les pièces polaires d’un électro-aimant taillé de façon convenable.
a) Atomes possédant seulement un moment cinétique de spin S = 1/2
L’expérience a été faite par STERN et GERLACH sur des atomes d’argent dans l’état fondamental 2S1/2. Elle a pu être réalisée depuis avec d’autres atomes dans le même état 2S1/2 : Na, K, H, Li, . . . On constate qu’en l’absence de champ, les atomes d’argent viennent se condenser sur une plaque froide en formant une seule tache; si on applique un champ uniforme cette tache se dédouble en deux taches distinctes symétriques par rapport à la tache initiale correspondant à deux faisceaux distincts d’atomes. Les deux faisceaux proviennent certainement de deux orientations distinctes du moment magnétique de l’atome, c’est-à-dire à deux valeurs de q dans l’équation 9.4. Les deux valeurs q = 0 et q = p viennent immédiatement à l’esprit étant donné l’aspect symétrique des deux taches. Chacune des deux catégories d’atomes est déviée par la force Fz ou - Fz.
L’expérience de STERN et GERLACH montre donc que le moment magnétique de spin peut s’orienter dans deux positions seulement par rapport à un champ magnétique : dans le sens du champ et dans le sens opposé au champ.
Nous comprenons facilement que le moment magnétique s’oriente dans le sens du champ car c’est ce que ferait un petit aimant. Il est plus difficile d’admettre que le moment magnétique s’oriente dans le sens opposé, ce qui correspond à une position d’équilibre instable pour le petit aimant. Il faut cependant croire que cette position est stable pour l’atome puisque l’intensité des deux taches est la même. À l’aide d’un raisonnement calqué sur celui utilisé au chapitre 3 dans le cas de la déflexion électrique des électrons, on peut relier la déviation z du faisceau et la force Fz. La connaissance de Fz entraîne celle de M car dH/dz est connu à partir de la géométrie de l’électroaimant. L’expérience permet donc également de mesurer le moment magnétique associé au spin. On trouve un magnéton de BOHR pour les atomes dans l’état 2S1/2.
b) Atomes dans un état quelconque
Un atome dans un état quelconque a un moment cinétique total donné par la valeur du nombre quantique J. Ce vecteur moment cinétique J total résulte de la composition des vecteurs dus au mouvement orbital, L, et au spin S, . De même, les moments magnétiques associés aux vecteurs L et S vont se composer et donner un moment magnétique total . Finalement, l’atome pourra être considéré comme un petit aimant dont le moment magnétique est M.
Que se passe-t-il si on fait l’expérience de STERN et GERLACH avec un atome dont le moment cinétique total est J ?
L’observation de 2 J + 1 taches concorde avec la théorie quantique de l’atome. En effet, le nombre quantique magnétique m qui s’est introduit dans le calcul de l’atome d’hydrogène définit la valeur de la projection du moment cinétique orbital de l’électron sur un axe et montre que la valeur de cette projection est quantifiée.
Pz = m h/2p ;
m = -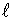 , -
, -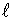 + 1, . . . , l
+ 1, . . . , l
Cette règle procure à l’électron 2 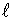 + 1 orbites d’orientation différentes, mais de même énergie. Le résultat de
l’expérience de STERN
et GERLACH montre que ce principe est également applicable au moment cinétique total J
d’un atome. Dans ce cas, J doit s’orienter de telle façon que :
+ 1 orbites d’orientation différentes, mais de même énergie. Le résultat de
l’expérience de STERN
et GERLACH montre que ce principe est également applicable au moment cinétique total J
d’un atome. Dans ce cas, J doit s’orienter de telle façon que :
Pz = M h/2p ; M = -J, - J + 1, . . . , J
Cela donne bien 2 J + 1 orientations possibles de J, donc 2 J + 1 orientations possibles du moment magnétique de l’atome. C’est ce phénomène général qui est appelé quantification spatiale. Le moment cinétique est quantifié, c’est-à-dire varie par quanta h/(2 p), et la projection du moment cinétique sur un axe est également quantifiée. Notons que le moment magnétique lui-même n’est pas quantifié.
c) Calcul du facteur g (facteur de LANDÉ)
Soit un atome dont les moments cinétiques sont déterminés par les nombres quantiques L, S, J. Les moments cinétiques correspondants sont les vecteurs PL, PS et PJ . Les moments magnétiques associés sont :
| 9.5 | 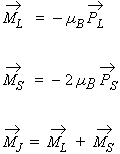 |
Les valeurs absolues des vecteurs PL et PS étant exprimées en unités h/(2 p). Le signe moins indique que les vecteurs sont de sens opposé. |
| 9.6 | ||
| 9.7 |
Par suite de la multiplication des vecteurs PL et PS par deux facteurs différents, le vecteur M n’aura pas l’orientation du vecteur P. C’est qui est orienté par le champ extérieur H. L’atome tournant autour du vecteur PJ, le moment magnétique résultant tourne aussi autour du vecteur PJ. L’atome semble avoir non pas le moment magnétique MJ, mais sa valeur moyenne; le moment µ projection du vecteur MJ sur le vecteur PJ. µ est donc le moment magnétique mesuré dans l’expérience de STERN et GERLACH. Calculons µ. Le théorème des projections donne (Fig. 9.3) :
| 9.7 9.8 |
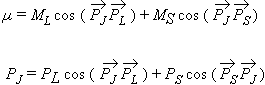 |
Soit en remplaçant ML et MJ par leurs valeurs tirées de 9.5 et 9.6 :
![]()
|
|
Figure 9.3. Calcul du facteur de LANDÉ.
En tenant compte de la valeur de PL tirée de 9.8 :
![]()
Cette expression s’écrit :
| 9.9 | µ = -g µB PJ = -g J µB; en fait µ = - g [J (J + 1)] 1/2 µB |
avec
![]()
La relation géométrique suivante permet de calculer g :
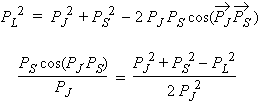
On peut prendre pour PJ , PS et PL soit les valeurs approchées mais commodes :
J h / (2p), S h / (2p) et L h / (2p), soit les valeurs exactes :
|
etc. |
etc. . .
Dans le second cas, on a la valeur exacte de g :
| 9.10 |
|
Cette formule montre que g dépend de J, S et L. Le tableau 9.2 indique plusieurs valeurs calculées du facteur de LANDÉ.
Tableau 9.2. Quelques facteurs de LANDÉ
| spin S | J | État S L = 0 |
P 1 |
D 2 |
F 3 |
G 4 |
| 1/2 | L + 1/2 L - 1/2 |
2 2 |
4/3 2/3 |
6/5 4/5 |
8/7 6/7 |
10/9 8/9 |
| 1 | L + 1 L L - 1 |
2 | 3/2 3/2 0/0 |
4/3 7/6 1/2 |
5/4 13/12 2/3 |
6/5 3/4 3/4 |
| 3/2 | L + 3/2 L + 1/2 L - 1/2 L - 3/2 |
2 | 8/5 26/15 8/3 - |
10/7 48/35 6/5 0 |
4/3 26/21 36/35 2/5 |
14/11 116/99 62/63 4/7 |
| 2 | L + 2 L + 1 L L - 1 L - 2 |
2 | 5/3 11/6 5/2 - - |
3/2 3/2 3/2 3/2 0/0 |
7/5 27/20 5/4 1 0 |
4/3 19/5 23/20 11/12 2/3 |
| 5/2 | L + 5/2 L + 3/2 L + 1/2 L - 1/2 L - 3/2 L - 5/2 |
2 | 12/7 66/35 12/5 - - - |
14/9 100/63 58/35 28/15 10/3 - |
16/11 142/99 88/63 46/35 16/15 -2/3 |
18/13 192/43 14/11 8/7 6/7 0 |
| 3 | L + 3 L + 2 L + 1 L L - 1 L - 2 L - 3 |
2 | 7/4 23/12 7/3 4 - - - |
8/5 33/20 7/4 2 3 - - |
3/2 3/2 3/2 3/2 3/2 3/2 0/0 |
10/7 59/42 41/31 13/10 7/6 5/6 -1/2 |
| En partie d’après Kuhn, H.G., Atomic Spectra, Longmans, Green & Co., Ltd, Londres (1964). | ||||||
Remarques :
1- Si S = 0, on a J = L et g = 1, on retrouve le cas particulier d’un atome possédant seulement un moment orbital dont le moment magnétique est :
ML =
-![]() µB
µB
2- Si L = 0, on a J = S et g = 2, on retrouve le cas particulier d’un atome possédant seulement un moment de spin dont le moment magnétique est :
![]()
3- Si g = 1 + 0/0, on a une indétermination. En réalité, cela survient lorsque la somme vectorielle
![]() =
= ![]() +
+ ![]() = 0
= 0
. Les moments magnétiques s’annulent et l’atome n’a pas de moment magnétique propre.
4- Si g = 0, le niveau correspondant n’est pas subdivisé en sous niveaux en présence de champ magnétique.
Les différentes possibilités d’orientation du moment magnétique atomique sont également observables de manière spectroscopique. Chronologiquement, c’est même la première observation qui en ait été faite. Lorsque l’atome émetteur est placé dans un champ magnétique, on assiste à un dédoublement des raies d’émission en plusieurs composantes dû à un dédoublement des niveaux d’énergie. C’est ce phénomène qui constitue l’effet ZEEMAN. Nous allons d’abord expliquer le dédoublement des niveaux d’énergie dans un cas simple (effet ZEEMAN normal), puis dans un cas plus complexe (effet ZEEMAN anormal).
L’effet normal (qui est cependant le plus rare) est observé lorsque le niveau d’énergie correspond à un spin S = 0, c’est-à-dire lorsqu’il s’agit d’un niveau simple (2 S + 1 = 1). Dans ce cas, le facteur g = 1 (voir l'équation 9.10). Le moment cinétique de l’atome est uniquement son moment orbital L et le moment magnétique a pour valeur :
µL = - µB L
Le signe moins indique que les vecteurs mL et L sont de signes opposés.
L’énergie que possède l’atome lorsqu’il est placé dans le champ magnétique est la somme de deux énergies :
EH = -
µL![]() = - µL H
cos q
= - µL H
cos q
q étant l’angle que fait le moment magnétique et le champ. On peut donc écrire l’énergie totale sous la forme :
E = En - µL H cos q
E = En + µL H cos q
Or, L cosq est la valeur en unité h/(2 p) de la projection du vecteur moment cinétique sur la direction du champ. On sait que cette valeur est quantifiée :
Pz = L (h/2p) cos q = M (h/2p)
d’où: L cos q = M avec M = - L, - L + 1, ...... ,+ L.
Finalement, l’énergie totale est :
| 9.11 | E = En + M µB H |
M pouvant prendre les 2 L + 1 valeurs précédentes (Fig. 9.4 et 9.5).
Le niveau d’énergie En est donc démultiplié en 2 L + 1 niveaux d’énergie différente. Ces 2 L + 1 niveaux sont dégénérés en l’absence de champ (H = 0), c’est-à-dire ont la même énergie. La séparation des niveaux correspondant à deux valeurs consécutives de M est constante :
EM + 1 - EM = µB H
Les niveaux sont donc également espacés selon le schéma donné pour L = 2.
Considérons une raie spectrale émise par transition entre deux niveaux simples EN et EM. Prenons par exemple deux états 1D2 et 1P1 (Fig. 9.6). Dans le champ magnétique, des transitions seront possibles entre les 5 niveaux 1D2 et les 3 niveaux 1P1. Si toutes les transitions étaient possibles, on devrait observer 7 raies différentes. On observe seulement trois raies. Il existe donc des transitions interdites. On peut montrer par un calcul théorique de la variation de moment dipolaire que la règle de sélection est :
DM = 0 ; ± 1 .
Cette règle permet bien d’obtenir les trois raies observées.
|
|
Figures 9.4. Dédoublement d’un niveau dans un champ magnétique.
|
|
Figures 9.5. Effet ZEEMAN normal sur l’atome d’hélium.
|
|
Figures 9.6. Effet ZEEMAN normal sur deux transitions observées dans le cadmium.
|
|
Figures 9.7. Effet ZEEMAN anormal sur le doublet D1 et D2 du sodium.
Dans la plupart des cas, une raie spectrale provenant d’un atome placé dans un champ magnétique est dédoublée en plus de trois composantes. Le nombre de composantes est d’ailleurs variable avec la nature de l’état initial et de l’état final, c’est-à-dire avec les valeurs de S, L et J. Cet effet est dû au facteur de LANDÉ g et a permis la première détermination de ce facteur. Le moment magnétique de l’atome dans un état quelconque est -g J µB. L’énergie de ce petit aimant dans le champ magnétique est donc g J µB H cos q, H et q ayant les mêmes significations que précédemment. L’énergie de l’atome sera donc donnée par :
E = En + g µB H cos q
Le produit cos q représente la valeur [en unité h/(2 p)] du moment cinétique dans la direction du champ de sorte que :
Em = En + M g µB H
M étant le nombre quantique magnétique. Ce nombre M varie par valeur h/2 p entre -J et +J. Le niveau initial En est donc dédoublé en autant de sous niveaux que de valeurs de M. Ces niveaux sont séparés par l’énergie constante :
Em + 1 - En = g µB H
Mais comme g dépend de L, S et J, les divers niveaux ne conduisent pas tous à la même séparation et la règle de sélection :
DM = 0 ; ± 1
toujours valable conduit en général à un nombre de raies possibles plus élevé. Ce nombre M varie par valeur h/2p entre les valeurs -J et +J. L’exemple des raies jaunes du sodium permet de comprendre facilement le mécanisme (Fig. 9.6). L’une des raies du doublet (2P1/2 - 2S1/2) forme un groupe de 4 raies tandis que l’autre (2P3/2 - 2S1/2) forme un groupe de 6 raies.
Tableau 9.3. Notation atomique
| Nombre quantique de moment cinétique |
Notation | Valeurs |
orbital |
L | 0 1 2 3 . . . |
Notation |
X | S P D F . . . |
de spin |
S | 1/2 par électron célibataire |
| Total | J | |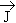 | = | | = |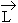 | + |
| + |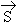 | | |
Multiplicité du niveau 2 s + 1
|
X |
J |
Compositions vectorielles des moments cinétiques (dégénérescence). |
Rappel : la dégénérescence est égale à 2 J + 1 façons de faire la somme vectorielle.
Transitions permises :
Dl = ± 1, DJ = 0 ou ± 1, DS = 0 |
|
Le moment magnétique de l’atome, en présence d’un champ magnétique externe prend des orientations privilégiées de telle manière que le moment magnétique de l’atome est égal à un nombre entier de magnéton de BOHR. La mise en évidence de cette quantification spatiale est observée lors de la déviation subie par un faisceau d’atome de sodium, par exemple, circulant entre les mâchoires d’un électro-aimant développant un champ intense. Le faisceau originel se dédouble en 2J + 1 faisceaux. Par ailleurs, l’effet ZEEMAN normal (et anormal) permet de " voir " ces orientations à travers le dédoublement de raies d’émission résultant d’un saut électronique à l’intérieur du nuage électronique.
|
| 9.1 | L’atome de mercure dispose des termes spectraux suivants : 1S0, 3P0, 3P1, 3P2, 1P1, 3S1, (dans l’ordre croissant de l’énergie). a- Dites quelles sont les transitions permises ? b- En présence de champ magnétique on étudie la transition 1P1 ® 1S0, dites en combien de raies la raie originelle est subdivisée ? Dessiner sur un axe gradué en énergie, la succession des raies.
|
| 9.2 | Le nickel gazeux à 25 °C présente les états électroniques suivants :
a- Dites quelles sont les transitions électroniques observables. b- En présence de champ magnétique intense, on étudie la transition 3F3 ® 3D2 , dites en combien de raies, la raie initiale sera divisée. c- De la même manière, on étudie la transition 3F2 ® 3D3 en présence du champ magnétique. En combien de raies la raie initiale sera-t-elle divisée ? Dans ce cas, sur un axe gradué en énergie, positionnez les raies observées et indiquez les intensités relatives de ces raies. |
| 9.3 | Les niveaux possibles d’énergie pour l’atome de calcium sont les suivants (dans l’ordre croissant d’énergie) : 1S0, 3P2, 3P1, 3P0, 3D3, 3D2, 3D1, 1D2, 1P1,... a- Dites quelles sont les transitions permises et pourquoi elles le sont. b- On étudie la transition 1P1® 1S0 (422,67 nm), dites de combien de raies sera constituée la transition en présence de champ magnétique. c- Même question pour la transition 3D1 ® 3P2. |
| 9.4 | Le zinc a une transition étiquetée 3S1 ® 3P1. Combien de raies seront observées en présence de champ magnétique? Dessinez à l’échelle, sur un axe gradué en énergie, la succession des raies. |
- - - - - - - - - - - - - - - -
Pour en savoir un peu plus
Liens intéressants :
La biographie de Pieter Zeeman ainsi que d’autres éléments sont disponibles sur le site des Prix Nobel :
https://www.nobelprize.org/prizes/physics/1902/zeeman/biographical/ (visité le 2019-02-19).
Par ailleurs, le siteWeb déjà mentionné de la Georgia State University présente des "diapos" intéressantes relativement à l’effet Zeeman, au facteur de Landé et à beaucoup d’autres choses. Ce site, qui peut aussi être avantageusement utilisé comme glossaire à travers son index, a été construit par Carl R. (Rod) Nave :
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html (visité le 2019-02-19).
Note : on se servira de l’index pour trouver les éléments rechercher : Zeeman effects.
Dernière mise à jour : 2021-07-23.
XXXXXXXXXXXXXXXXXX