|
|
et |
|
CHAPITRE I
|
La thermochimie étudie la capacité qu’ont les molécules d’emmagasiner de l’énergie et de l’échanger avec d’autres molécules dans des processus physiques. Elle étudie aussi la production ou l’absorption d’énergie au cours des réactions physiques et chimiques. Avant d’entrer dans des considérations très détaillées, il convient d’établir ce qu’est une capacité calorifique. Quels sont les facteurs qui influencent la capacité de stockage de l’énergie par les molécules ? Comment définit-on ces capacités ?
|
1. Préambule
Les premières mesures thermodynamiques ont commencées par des mesures de capacités calorimétriques. L’idée est de mesurer la capacité calorifique des éléments et des composés chimiques. Le principe de construction du calorimètre et sa disponibilité ont fait que ces mesures sont devenues rapidement accessibles. Ces résultats (les premiers ont près de deux cents ans) deviendront la base expérimentale de la thermodynamique.
2. Les capacités calorifiques
Définition :
La capacité calorifique est la quantité de chaleur qu'il faut fournir pour élever de un degré la température d'une substance.
Bien évidemment, l’accumulation d’énergie par les molécules dépend de plusieurs facteurs dont la température. Une façon commode de suivre cette accumulation d’énergie interne est de mesurer les capacités calorifiques ou encore les chaleurs latentes. On définit deux grandeurs macroscopiques que sont les capacités calorifiques à pression et à volume constant soit respectivement CP et CV. Les grandeurs molaires sont surmontées d’une barre horizontale,
|
|
et |
|
Par définition, dans le vieux système d’unités des chimistes, la calorie était la quantité d’énergie qu’il fallait fournir à un gramme d’eau pour élever sa température de 14,5 à 15,5 ºC. En d’autres termes, la capacité calorifique de l’eau à 15 ºC est de 1 cal/g. Par définition (voir un précédent cours de thermodynamique):
| [1.1] |
ou mieux encore
![]()
La capacité calorifique à pression constante, Cp, est égale à la dérivée partielle de l'enthalpie par rapport à la température à pression constante. De même, La capacité calorifique à volume constant, Cv, est égale à la dérivée partielle de l'énergie interne par rapport à la température à volume constant.
La quantité de chaleur requise pour élever n moles de substances de la température T' à la température T" à pression constante est donc :
| [1.2] | 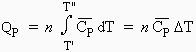
|
si la capacité calorifique molaire à pression constante,
![]()
est indépendante de T (constant) sur l’intervalle de température considéré. De la même manière,
| [1.3] | 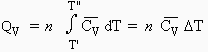
|
si la capacité calorifique molaire à volume constant, la grandeur
![]()
est indépendante de T (constant) sur l’intervalle de température considéré. On sait aussi que :
H = E + PV ou encore E = H - PV
| [1.4] |
|
a- Pour les solides et les liquides, la variation du produit PV avec la température est négligeable. Par conséquent, en phase condensée, les capacités calorifiques à volume et à pression constants ont des valeurs voisines :
CP = CV .
Loi de DULONG (1785-1838) et PETIT (1791-1820) - loi énoncée en 1819 :
La
capacité calorifique molaire des divers éléments à la température normale |
On remarquera que cette valeur est voisine de 3 R. Le tableau 1.1 montre qu’effectivement la loi de DULONG et PETIT s’applique à l’ensemble des solides monoatomiques comme les métaux. On observe cependant que pour le carbone et le bore, la capacité calorifique molaire est plus faible que celle prévue par cette loi.
Tableau 1.1.
Capacités calorifiques molaires à pression
constante de quelques
solides
exprimées en [J/(mol·K)]
Substances |
(300 K) |
(800 K) |
Substances |
(300 K) |
|
Loi de DULONG et PETIT |
Loi de NEUMANN et KOPP |
||||
Carbone (diamant) |
6,0 |
CuO |
46,0 |
54,0 |
|
Bore |
12,0 |
FeO |
50,6 |
54,4 |
|
Calcium |
24,7 |
MgO |
37,7 |
48,1 |
|
Argent |
25,5 |
28,0 |
ZnO |
44,8 |
50,6 |
Aluminium |
24,3 |
30,5 |
PbO |
47,4 |
|
Chrome |
24,3 |
28,9 |
AgCl |
54,4 |
|
Cuivre |
24,3 |
27,6 |
Ag2S |
75,3 |
90,4 |
Fer |
24,7 |
37,2 |
Cu2O |
68,6 |
|
Magnésium |
23,8 |
30,5 |
CuCl2 |
77,75 |
|
Phosphore |
23,8 |
SiO2 |
56,1 |
71,5 |
|
Plomb |
27,2 |
PbCl2 |
77,4 |
||
Zinc |
25,1 |
Al2O3 |
83,7 |
120,5 |
|
Uranium |
27,9 |
Cr2O3 |
110,5 |
125,1 |
|
Loi de NEUMANN et KOPP :
La chaleur spécifique molaire des combinaisons chimiques solides est égale à la somme des chaleurs spécifiques molaires des éléments composants. |
À nouveau, le tableau 1.1 montre la validité de cette loi. La capacité calorifique des composés formés de deux atomes devrait être le double de celle observée pour les métaux, soit 50 J·mol-1, celle des composés triatomiques devrait être de 75 J·mol-1… La loi est relativement bien suivie, sauf pour MgO, SiO2 et Al2O3, … pour des composés formés d’éléments légers.
En supposant qu’au sein du solide, les atomes peuvent vibrer autour d’une position d’équilibre, EINSTEIN (1879-1955) a trouvé une relation entre cette fréquence de vibration n, vibration unique, et la capacité calorifique à volume constant. La loi énoncée en 1906 est la suivante :
La capacité calorifique d’un solide est donnée par une relation déduite des mouvements vibratoires du réseau cristallin . |
| [1.5] |
|
Dans cette équation h est la constante de PLANCK, k la constante de BOLTZMANN, R est la constante des gaz parfaits et q = hn/k .
En 1912, DEBYE a repris l’étude faite par EINSTEIN. Il a obtenu une relation plus représentative de la réalité, donc plus satisfaisante. La valeur de la capacité calorifique molaire du solide prend la forme suivante :
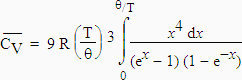
Dans cette équation, la valeur de x est défini par la relation :
x
=
hnm/k =
qD
et qD est la température de DEBYE. En outre DEBYE suppose que le solide peut vibrer avec des fréquences allant de zéro à une valeur maximum nm.
Tableau 1.2. Température (K) de DEBYE pour quelques éléments
Substances |
qD |
qD |
qD |
Carbone (diamant) |
1840 |
2230d - 2200e |
- - |
Béryllium |
1000 |
- - |
- - |
Sodium |
159 |
- - |
- - |
Aluminium |
398 |
385 – 426 |
399 |
Potassium |
99 |
- - |
- - |
Fer |
420 |
428 - 464 |
467 |
Cuivre |
315 |
321 - 344,5 |
- - |
Znc |
235 |
205 - 300 |
- - |
Molybdène |
379 |
379 - 440 |
- - |
Argent |
215 |
- - - 225 |
212 |
Cadmium |
160 |
129 – 186 |
168 |
Étain |
160 |
127 - - - |
- - |
Platine |
225 |
240 - - - |
226 |
Or |
180 |
162 - 165 |
|
Plomb |
88 |
96 - - - |
72 |
| a- Équation générale de Debye; b- équation de Debye réduite aux basses températures; c- Valeurs calculées à partir des constantes d’élasticité des solides; d- Valeurs tirées de Handbuch der Experimental Physik - Table XIV-2 - vol. 8 (Eucken); e- Valeurs tirées du Handbook of Chemistry, 50e éd., page D-129. | |||
Cette loi est complexe. La capacité calorifique molaire à volume constant peut néanmoins être calculée à toute température pourvu que l’on connaisse qD la température caractéristique de la substance. qD est aussi appelée la température de DEBYE de la substance. À basse température cette loi de DEBYE peut être simplifiée. Si la température T est plus petite que la température de DEBYE, T << qD :
| [1.6] |
|
À haute température, lorsque la température T est
beaucoup plus grande que la température de DEBYE, la capacité calorifique
molaire à volume constant tend vers la valeur 3 R, où R est la
constante des
gaz parfaits.
Tableau 1.3. Loi de DEBYE et capacités calorifiques molaires (cal/mole) observées pour l’aluminium
Température (K) |
|
|
54,8 |
1,127 |
1,11 |
70,0 |
1,851 |
1,88 |
84,0 |
2,446 |
2,51 |
112,4 |
3,502 |
3,54 |
141,0 |
4,183 |
4,23 |
186,2 |
4,833 |
4,87 |
257,5 |
5,382 |
5,35 |
278,9 |
5,499 |
5,42 |
296,3 |
5,526 |
5,48 |
Les écarts observés à la loi de DULONG et PETIT pour les éléments légers trouvent ici leur explication. En effet, les composés légers ont une capacité calorifique qui n'atteint 25 J/mol/K qu’à température élevée. La figure 1.1 montre l’augmentation des valeurs des capacités calorifiques pour le cuivre et pour le carbone. Alors qu’à 300 K le cuivre a déjà une capacité calorifique de 24 J/mol/K, le carbone n’atteint cette valeur que vers 1500 K. À haute température, lorsque la température de l'échantillon est beaucoup plus grande que la température de DEBYE, T >> q, la capacité calorifique molaire à volume constant est égale à 3 fois la constante des gaz parfaits.
|
|
Figure 1.1. Variation de la capacité calorifique molaire à
volume constant
pour le carbone et le cuivre solide.
Tableau 1.4. Températures caractéristiques de DEBYE pour quelques molécules
Molécules gazeuses |
H2 |
N2 |
O2 |
Cl2 |
NO |
CO |
HCl |
qv (K)* |
6130 |
3350 |
2224 |
801 |
2705 |
3085 |
4200 |
Solides cristallins |
KCl |
AgCl |
NaCl |
AgBr |
|||
qs (K) |
227 |
183 |
281 |
144 |
|||
* Dans le cas des molécules gazeuses, qv = hn/k égalité dans laquelle n est une fréquence caractéristique de la vibration. |
|||||||
b) Pour les gaz parfaits :
| [1.7] |
|
Le tableau suivant permet de vériofier cette relation.
Tableau 1.5. Valeurs des capacités calorifiques molaires [J/(mole · K)]
pour quelques gaz entre 15 et 25 ºC
Gaz |
|
|
|
Gaz |
|
|
|
Hg |
20,9 |
12,54 |
8,36* |
NH3 |
36,78 |
27,80 |
8,98* |
Ar |
20,77 |
12,46 |
8,31 |
CO2 |
36,91 |
28,42 |
8,49 |
He |
20,77 |
12,46 |
8,31 |
H2O |
36,24 |
27,04 |
9,20 |
N2 |
28,95 |
20,61 |
8,34 |
H2S |
34,69 |
25,92 |
8,77 |
O2 |
29,36 |
21,03 |
8,33 |
CH4 |
35,53 |
27,17 |
8,36 |
H2 |
28,61 |
20,31 |
8,30 |
NO2 |
37,95 |
29,39 |
8,56 |
CO |
29,13 |
20,82 |
8,30 |
C2H2 |
43,68 |
35,11 |
8,57 |
NO |
29,68 |
21,32 |
8,36 |
C2H4 |
42,85 |
34,28 |
8,57 |
HCl |
29,43 |
20,90 |
8,53 |
C2H6 |
51,62 |
43,05 |
8,57 |
*Note : R = 8,314 J/(mol·K).
On a déjà vu dans un cours de chimie-physique que la capacité calorifique molaire est égale à 1,5 fois la valeur de la constante des gaz parfaits. Cette relation est vraie dans le cas des gaz monoatomiques dont les seuls degrés de libertés sont ceux de la translation selon chacun des trois axes du trièdre trirectangle Ox,Oy et Oz. En remplaçant dans l'équation [1.7], on obtient :
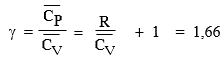
Le rapport des capacités calorifiques molaires isobare et
isochore est appelé le coefficient
isentropique
g.
Pour un gaz
diatomique, aux trois degrés de
liberté de translation, il faut ajouter deux degrés de liberté de rotation.
En effet, si la molécule est située sur l’axe Ox, elle peut tourner sur
elle-même autour des deux axes perpendiculaires à l’axe de la molécule.
Dans ce cas,
![]()
En effet le
principe d’équipartition de l’énergie stipule qu’à la température T, il y a une
quantité d’énergie 1/2 RT disponible par degré de liberté.
Par conséquent,
![]()
Les molécules gazeuses non linéaires peuvent tourner sur
elles-mêmes selon les trois axes.
L’énergie disponible est maintenant 3RT.
Le rapport isentropique devient :
![]()
Le tableau 1.5 montre qu’effectivement les valeurs numériques des capacités calorifiques molaires à volume constant pour les gaz monoatomiques, biatomiques et plusieurs autres correspondent bien aux valeurs indiquées plus haut. Il en est de même des rapports des capacités calorifiques à pression et à volume constant. Il y a aussi des divergences. Dans certains cas des mouvements de vibration viennent s’ajouter compliquant ainsi les résultats observés.
|
|
Figure 1.2. Variation de CV avec la température pour un gaz réel.
En fait, pour un gaz, la capacité calorifique à volume constant varie profondément avec la température (Fig. 1.2). Si un gaz accumule facilement, c’est-à-dire à basse température, de l’énergie cinétique, il doit être porté à plus haute température pour accumuler de l’énergie dans son réservoir rotationnel. Cela est faisable à la température ordinaire. Les niveaux excités d’énergie vibrationnelle ne sont généralement atteints qu’à plus de 1000 ºC.
Note complémentaire
dans un gaz, le rapport des capacités calorifiques molaires est directement accessible.
En effet la vitesse du son, u,
dans un gaz est reliée à ce rapport par la loi de NEWTON.
Pour un gaz parfait, ce rapport est tel que :
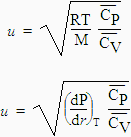 |
|
|
Pour un
gaz réel : |
Dans cette expression le rapport (dP/dr)T représente la variation de la pression en fonction de la masse volumique à température constante.
Rappel historique
Il faut rappeler ici la définition de la calorie, unité thermique jadis utilisée par les physico-chimistes. La calorie est l’énergie nécessaire pour chauffer un gramme d’eau de la température de 14,5 à 15,5 °C. L’équivalent mécanique de la calorie est de 4,18 joules.
3. Influence de la température sur les capacités calorifiques
On peut sans douter et on l’a déjà vu à la figure 1.1, les capacités calorifiques d’un composé varient avec la température : Cp = f (T) et Cv = f (T). Il en est bien entendu de même avec les grandeurs molaires. On sait calculer théoriquement ces valeurs (voir, par exemple un cours de mécanique statistique). Historiquement, les mesures des capacités calorifiques étant aisément accessibles et mesurables par calorimétrie, on les a plutôt mesurées. Ces données apparaissent, par exemple, dans le " Handbook of Chemistry " sous la forme de coefficients applicables à des formules du type
|
|
= a' + b' T + c' T2 + d' T3 |
ou encore
|
|
= a + b T + c T-2 |
Les deux tableaux qui suivent montrent des exemples de ces valeurs.
Tableau 1.6a. Variations de la capacité calorifique molaire à pression constante avec la température de quelques molécules :
| |
= a' + b' T + c' T2 + d' T3 (cal·K-1·mol-1) |
| Molécules gazeuses | Température (K) | a' | b '(× 103) | c''(×107) | d'(× 109) |
| Hydrogène | 300-2500 | + 6,62 | + 0,81 | ||
| O2 (g), N2 (g) | 300-2500 | + 6,76 | + 0,606 | + 1,3 | |
| Carbone (graphite) | 300-1400 | + 2,67 | + 2,617 | - 1,169 | |
| Oxyde de carbone | 300-2500 | + 6,60 | + 1,20 | ||
| Gaz carbonique | 300-1500 | + 5,166 | + 15,177 | - 95,78 | + 2,26 |
| Eau | 300-1500 | + 7,219 | + 2,374 | + 2,67 | |
| Ammoniac | 300-1000 | + 6,189 | + 7,887 | - 7,28 | |
| Méthane | 300-1500 | + 3,422 | + 17,845 | - 41,65 | |
| Hydrogène sulfuré | 300-1800 | + 6,955 | + 3,675 | + 7,40 | - 0,585 |
| Réf.: Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, 4e éd., MacMillan Co., New York, 1967. | |||||
Tableau 1.6b. Variations de la capacité calorifique molaire à pression constante avec la température de quelques molécules :
|
|
= a + b T + c T-2 |
| Molécules | a J·K-1·mol-1 |
b
(× 103) J·K-2·mol-1 |
c
(×10-5) J·K·mol-1 |
| He, Ne, Ar, Kr | + 20,79 | 0 | 0 |
| Hydrogène (g) | + 27,28 | + 3,26 | + 0,50 |
| Oxygène (g) | + 29,96 | + 4,18 | - 1,67 |
| Azote (g) | + 28,58 | + 3,76 | - 0,50 |
| C (graphite) | + 16,86 | + 4,77 | - 8,54 |
| S (g) | + 22,01 | - 0,42 | + 1,51 |
| S2 (g) | + 36,48 | + 0,67 | - 3,76 |
| CO (g) | + 28,41 | + 4,10 | - 0,46 |
| CO2 (g) | + 44,22 | + 8,79 | - 8,62 |
| H2O (g) | + 30,54 | + 10,29 | 0 |
| NH3 (g) | + 29,75 | + 25,10 | - 1,55 |
| CH4 (g) | + 23,64 | + 47,86 | - 1, 92 |
| Source : Thermodynamics, 2e éd., McGraw-Hill Book Co., New York 1961. | |||
|
|
L’exemple du fer est intéressant. Entre 300 et 2000 K, on s’attend à observer une fonction de la capacité calorifique, CP, qui varie avec la température T. En outre, puisque le fer change de structure cristalline à 1183 et à 1673 et qu’il fond à 1812 K, on s’attend à observer des discontinuités. Ce qui est bien le cas. Mais on observe aussi un comportement particulier vers 1030 K. Le fer ne change pas de structure entre 300 et 1183 K : sa maille est cubique centré et on l’appelle le fer a. La même structure se retrouve entre 1673 et 1812 K. Entre 1183 et 1673, il cristallise dans le système cubique à faces centrées : fer g. Vers 900 K jusqu’à 1033 K, la valeur de la capacité calorifique à pression constante CP croît de manière significative (Fig. 1.3). Passé cette valeur de 1033 K, CP décroît rapidement. Ce comportement correspond à une transformation magnétique. En dessous de 1033 K (760 °C), les moments magnétiques des atomes interagissent l’un sur l’autre : ils ont tendance à s’orienter dans une direction commune (Voir le comportement ferromagnétique dans un cours de physique atomique). Au dessus de cette température cette orientation disparaît. La température de 1033 K correspond au point de CURIE. On voit donc que la variation des capacités calorifiques avec la température donne des informations importantes sur la structure, cristalline dans ce cas.
|
|
Figure 1.3. Variations de la capacité calorifique du fer avec la température.
4. Chaleurs latentes de changement de phase
C’est l’énergie requise pour qu’un composé puisse changer de phase sans changement de température. Par exemple, l’énergie requise pour les changements de phase de l’eau sont les suivants :
fusion : 80 cal·g-1 ou 334,4 J/g; vaporisation : 537 cal·g-1ou 2245 J/g.
Il s’ensuit que la chaleur latente de solidification est de - 80 cal·g-1 (ou encore - 6 020 J·mol-1). Il faut bien noter que ces changements de phase se font sans changement de température. Il faut aussi faire la différence avec les capacités calorifiques qui s’expriment en cal·g-1·degré-1 ou en J·mol-1·degré-1. On montrera plus loin que ces chaleurs latentes de changement de phase peuvent être obtenues au moyen de la loi de CLAPEYRON :
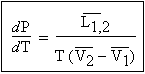
Dans cette égalité P et T sont les pression et température pour lesquelles les deux phases coexistent, L1,2 représente la chaleur latente pour que le composé puisse passer de la phase 1 à la phase 2 tout en demeurant à la température de changement de phase T.
![]()
représentent les volumes molaires de la substance dans chacune des deux phases. On aura compris que la chaleur latente de changement de phase, L1,2, est une notion similaire à l’enthalpie de changement de phase, DHvap, par exemple.
Table 1.7. Quelques chaleurs latentes molaires de changement de phase
Composé |
Tfus |
|
Tvap |
|
Tsubl |
|
Aluminium Fer Molybdène Mercure Azote Oxygène Chlore Eau Eau lourde CCl4 Toluène |
660 1 540 2 610 - 39 -210 - 219 - 101 0,0 4 - 23,0 - 95,0 |
10 14 28 2,3 0,36 0,22 6 6,02 6 |
2 450 3 000 5 560 357 - 196 - 183 - 35 100,0 101 76,5 110,6 |
291 351 590 59 2,8 3,4
40,4
32 38 |
326 416 658 64
50 52 |
|
En kJ/mol. Tiré en partie de Aylward & Findlay, SI, Chemical Data, John Wiley & Sons, 2ème éd., 1974. |
||||||
| 5- Conclusions
On définit les capacités calorifiques à volume ou à pression constante, Cv et Cp. Les capacités calorifiques dépendent de la température: elles croissent avec l’augmentation de la température. Cette augmentation traduit l’accumulation de l ’énergie dans les mouvements de translation, de rotation, de vibration, … des molécules. On définit également les chaleurs latentes de changement de phase (sans changement de température). Théoriquement, on peut calculer ces capacités calorifiques (lois de DEBYE et d’EINSTEIN).
|
6.1 Le cas de l'eau
À partir des données apparaissant dans ce chapitre, calculez en calories ainsi qu’en joules la quantité d’énergie requise pour chauffer 100 g de glace à la température de - 5 ºC et la transformer en eau vapeur à 120 ºC.
On donne aussi les capacités calorifiques molaires suivantes ainsi que la capacité calorifique de la glace :
- fusion : 6 020 J/mol ; vaporisation : 40 400 J/mol ;
- capacité calorifique de la glace : 2090 J/(kg · °).
Réponse : 757,0 kJ
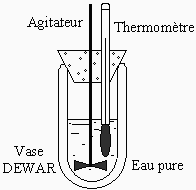
6.2 CalorimétrieOn veut déterminer la capacité calorifique par gramme d’un composé métallique inconnu (58,963 g). On dispose pour cela d’un calorimètre (voir figure) et d’un morceau de cuivre (72,256 g) de capacité calorifique égale à 24,46 J·°C-1·mol-1.
On procède à l’expérimentation de la manière suivante : on plonge chaque morceau solide dans de l’acétone à ébullition (Téb = 56,20 ºC) et l’on attend que l’équilibre thermique soit atteint. On plonge ensuite chaque morceau dans le calorimètre et l’on note la variation de température.
Température initiale (ºC) |
Température finale (ºC) |
|
Exp. A (cas du cuivre) |
22,32 (T1) |
24,01 (T2) |
Exp. B (composé inconnu) |
24,50 (T3) |
26,41 (T4) |
6.3 Réaction du gaz à l'eau
Soit à étudier la réaction :
|
CO2 (g) + H2 (g) |
|
CO (g) + H2O (g). |
Cette réaction est endothermique et KP croît avec la température.
Les données expérimentales sont les suivantes :
KP(686 ºC) = 0,534 et KP(986 ºC) = 1,571
À partir des valeurs de la capacité calorifique molaire à pression constante
![]()
apparaissant dans le tableau I.6b, calculer les valeurs
| et |
Pour en savoir un peu plus
David N. Blauch, Collège Davidson, Caroline du Nord, propose
une description de plusieurs expériences relatives à des mesures de
calorimétrie en effectuant des mesures virtuelles sur le site visité le
2019-02-03 :
http://www.chm.davidson.edu/ChemistryApplets/calorimetry/index.html
Dernière mise à jour : 2021-07-08.