CHAPITRE VII

CHAPITRE VII

ÉQUILIBRES CHIMIQUES

Après avoir bien compris les propriétés des principales fonctions thermodynamiques et leurs applications aux corps purs, on peut maintenant envisager l’application de ces fonctions aux réactions chimiques.

Questions :
- Comment peut relier la variation de l’énergie libre et les concentrations des réactifs et des produits dans un mélange en réaction ?
- Quelles sont les lois qui gouvernent les réactions et en particulier les équilibres chimiques ?

Objectifs :
- Connaître la règle de la variance et comment l'utiliser ;
- Comrendre la réaction d'un système lorsqu'il est soumis à une contrainte.

1. Introduction

Soit le mélange de méthanol et d’acide acétique. Laissé à lui-même, il réagit et se transforme partiellement à la température normale en acétate de méthyle et en eau. Si l’on mélange au contraire de l’acétate de méthyle et de l’eau, le système va évoluer vers la formation de méthanol et d’acide acétique. Si, en outre, on a pris soin dans chacun des deux cas de réaliser des mélanges équimoléculaires, on obtient le même mélange final.

CH₃OH + CH₃COOH CH₃COOCH₃ + H₂O

Les deux systèmes précédents évoluent l’un vers l’autre et atteindront un état d’équilibre dynamique. Loin d’être figés, les réactifs continuent de réagir. Il y a donc réactions directe (de gauche à droite) et indirecte (de droite à gauche) de façon ininterrompue. On dit aussi qu’il y a équilibre entre deux réactions. Les vitesses des deux réactions étant identiques, on obtient en apparence un état de non réaction.

Définitions

On appelle mélange tout système constitué d’au moins deux corps purs. Cette définition ne présume pas que les corps purs se dissolvent ou non mutuellement l’un dans l’autre. Par exemple, si la mixtion de l’eau et du pentane forme un mélange, il en est de même du chlorure de sodium, NaCl, immergé et donc solubilisé dans de l’eau.

On appelle équilibre homogène tout mélange qui résulte en la formation d’une seule phase solide, liquide ou gazeuse. Cette phase est homogène : ses propriétés sont identiques quel que soit le lieu considéré à l’intérieur de cette phase. Par exemple, a-pinène + b-pinène constitue une phase homogène organique. Comme les réactifs ne réagissent pas entre eux, il n’y pas d’équilibre chimique, mais seulement un équilibre physique. Le mélange de nitrate de potassium et de chlorure de sodium en solution aqueuse conduit à un équilibre chimique :

NaCl + KNO₃ KCl + NaNO₃

On appelle équilibre hétérogène tout mélange qui conduit à la formation d’un équilibre chimique faisant intervenir au moins deux phases homogènes. La dissolution d’iode dans le mélange eau - tétrachlorure de carbone conduit à une distribution d’iode entre les deux solvants. Il y a équilibre physique. Par contre, le mélange carbone graphite + bioxyde de carbone gazeux forme l’équilibre chimique hétérogène suivant :

C (graphite) + CO₂ (g) 2 CO (g)

2. Rappels - La règle des phases

2.a Définitions

a- phase j : Une phase est toute partie homogène d’un système physiquement distincte des autres parties dont elle est séparée par des surfaces de délimitation bien définies.

b- nombre de composants C :

Chaque phase contient un nombre d’espèces bien défini. Le nombre de composants est ce nombre d’espèces diminué du nombre de relations chimiques qui les relient.

Nota : ne pas confondre composant et composé!

c- variance u : Lorsque le nombre de composants d’un système et les composants de chacune des phases sont précisés, c’est le nombre de facteurs qu’il faut préciser pour que l’équilibre soit défini.

Nota : la variance est aussi appelée le nombre de degré de liberté du système.

2.b Calcul théorique de la variance

a- nombre de facteurs :

i- Température et pression : 2

ii- S’il y a C composants dans une phase, il a C - 1 concentrations indépendantes puisque S_iC_i = 1

Si j est le nombre de phases du système, il y aura j(C - 1) concentrations indépendantes.

b- nombre de relations :

i- Pour un composant il y a j - 1 relations thermodynamiques qui relient les quantités partielles molales entre les j phases. Comme il y a C composants, il y aura C (j - 1) relations thermodynamiques (voir tableau 7.1).

c- variance

La variance u est égale au nombre de facteurs diminué du nombre de relations :

u = 2 + j(C - 1) - C (j - 1)

[7.1] Þ

u = C + 2 - j

Tableau 7.1. Représentation schématique d’un système de n composés en équilibre
dans j phases

Phase 1	Phase 2	Phase 3		Phase j		Phase j
[A]₁	[A]₂	[A]₃	...	[A]_j	...	[A]_f
[B]₁	[B]₂	[B]₃	...	[B]_j	...	[B]_f
[C]₁	[C]₂	[C]₃	...	[C]_j	...	[C]_f
[D]₁	[D]₂	[D]₃	...	[D]_j	...	[D]_f
[I]₁	[I]₂	[I]₃	...	[I]_j	...	[I]_f
[N]₁	[N]₂	[N]₃	...	[N]_j	...	[N]_f

2.c Cas particuliers

Dans le cas où la phase gazeuse n’intervient pas, le paramètre pression n’intervient pas puisque les solides et les liquides sont réputés incompressibles :

u = C + 1 - j

C’est le cas des courbes de fusion, des transformations allotropiques.

3. Constantes thermodynamiques à l’équilibre ou d’équilibre

Soit la réaction a A + b B 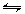L + m M

[7.2]

Dans cette équation, a_A est l’activité du réactif A,...

Pour qu’il y ait équilibre, il faut que la variation d’énergie libre au cours de la réaction soit nulle :

[7.3]

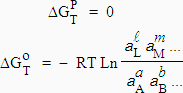À température donnée, la valeur du membre de droite de l’équation [7.3] est constante.

[7.4] Þ

K_a est la constante thermodynamique à l’équilibre et

[7.5]

à l’équilibre. Il faut noter que

K_a (réaction directe) = ¹ / _K_{_a} (réaction inverse)

4. Introduction des mesures K_P, K_c, K_y et K_g

4.a Relation entre K_a, K_P et K_g

[7.6] Dans un gaz, a = P g où

- a est l’activité ou encore appelé la fugacité,
- P est la pression partielle, et
- g est le coefficient d’activité

L’activité d’un constituant dans un gaz mesure en quelque sorte son influence réelle au sein du mélange gazeux, Si le mélange est idéal, l’influence réelle de chaque gaz est égale à sa fraction molaire. On remarque que cette idéalité s’amenuise au fur et à mesure que le mélange s’approche des conditions de liquéfaction ou encore que la pression totale s’accroît comme le montre le tableau suivant.

Tableau 7.2. Relation entre la pression et l’activité pour quelques gaz

P (atm)	Hydrogène (100 °C)		Ammoniac (200 °C)		Gaz carbonique (60 °C)
P (atm)	a (atm)	g	a (atm)	g	a (atm)	g
0 25 50 100 200 300 400 500	0,0 25,3 51,5 105 222 351 492 650	1,00 1,01 1,03 1,05 1,11 1,17 1,23 1,30	0,0 23,9 45,7 84,8 144 193	1,000 0,954 0,913 0,848 0,720 0,642	0,0 23,2 42,8 70,4 91,0 112	1,000 0,928 0,856 0,704 0,455 0,373
Extrait de Maron, S. H. & C. F. Prutton, Principles of Physical Chemistry, McMillan Comp., Ney York, 1965.

Loi de LEWIS :

L’activité d’un composé faisant partie d’un mélange gazeux est égale à la pression partielle de ce composé gazeux multipliée par le coefficient d’activité du gaz à la pression totale du mélange.

[7.7] a_i= P_i g_i = x_i P g_i où

- x_i est la fraction molaire du gaz i,
- P est la pression totale, et
- g_i est le coefficient d’activité.

NOTE: de l’équation [7.7] à la fin de ce chapitre, on a implicitement supposé que la pression de référence est la pression atmosphérique. Si ce n’est pas le cas, chaque valeur de P, P_i, P_L, … doit être remplacée par le rapport P/P₀, P_i/P₀, P_L/P₀,

[7.8] Þ K_a = K_PK_g

[7.9] où

Dans cette équation, K_a est la constante d’équilibre mesurée ou exprimée en fonction des activités de chacun des constituants de l’équilibre. K_P est la constante d’équilibre mesurée ou exprimée en fonction des pressions partielles. K_g est la constante d’équilibre mesurée ou exprimée en fonction des coefficients d’activité. Pour un gaz réel, cette valeur dépend de la pression totale. Pour un gaz parfait : K_g = 1 et K_a = K_P. En général, pour un gaz réel, K_g = 1 tant et aussi longtemps que la pression totale reste inférieure à 10 atmosphères.

4.b Expression de K_P et de K_C

En phase gazeuse, selon la loi de MARIOTTE,

[7.10] P = (n/V) R T = c R T où c représente le nombre de moles par unité de volume.

[7.11] Þ

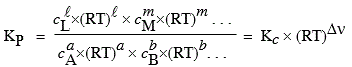Dans cette équation, regroupons les concentrations:

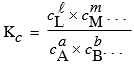
et Dn est la variation de molécularité de la réaction. Dn = + m + .. - a - b - . .

[7.12] K_P = K_c (R T)^Dn

Si Dn = 0, Þ (R T)^Dn = 1 et K_P = K_c ,

la transformation se fait à volume constant.

4.c Expression de K_Pen fonction de Kg

( y représente la fraction molaire) :

[7.13]

L'équation [7.12] peut se réécrire sous la forme :

[7.14] Þ

Comme c_x = n_x/V , y_x = n_x/n et PV = n R T

y_x = c_x (V/n) = c_x (RT / P)

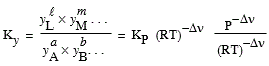
[7.15] K_y = K_P P^-Dn

Si à nouveau, la variation de molécularité de la réaction est nulle, Dn = 0, Þ K_y = K_P puisque P^-Dn= 1.

5. La loi de LE CHATELIER - BRAUN ou encore le principe de LE CHATELIER

Considérons un système à deux températures différentes T et T',

[7.5]

ou encore

Supposons que les températures T et T' soient proches de telle manière que les enthalpies et les entropies de réaction ne changent pas :

[7.16]

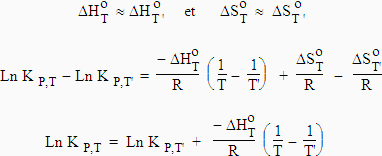1- Supposons que la réaction soit exothermique : la variation d’enthalpie est négative, DH < 0 et que T ' > T

Þ Ln K_P,T > Ln K_P,T'

Autrement dit, la constante d’équilibre décroît lorsque la température T croît : l’équilibre se déplace vers la gauche quand la température croît.

2- Supposons que la réaction soit endothermique : la variation d’enthalpie est positive DH > 0 et que T ' > T

Þ Ln K_P,T < Ln K_P,T'

Autrement dit, la constante d’équilibre croît lorsque la température T croît : l’équilibre se déplace vers la droite quand la température croît.

Dans chaque cas, pour contrer l’élévation de température, le système tend à absorber de l’énergie. Si l’on applique un stress à un système en équilibre, celui-ci réagit de manière à éliminer ce stress, de façon à annihiler la déformation imposée. Ce principe est aussi aisément vérifiable dans le cas où la déformation appliquée est une variation de pression (voir aussi LE CHATELIER).

6. Effet de gaz inerte

a) À haute pression, l’ajout d’un gaz inerte modifie les coefficients d’activité g_iet donc la valeur de la constante d’équilibre K_g.

b) À faible pression, il n’y a pas d’effet de cette nature (ou celui-ci est marginal). Il y a cependant changement des pressions partielles tout comme de la pression totale.

6.a Si le système opère à volume constant

Écrivons l’expression de la constante K_P :

[7.17]

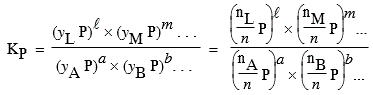car y_L = n_L / n et n = n_A + n_B + ... + n_L + n_M + .... Donc,

[7.18]

[7.19]

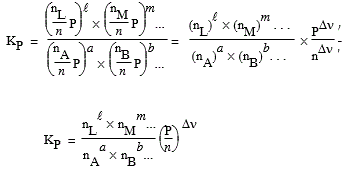Si le volume V est constant, quand le nombre n croît, la pression P croît également et n est proportionnel à P : n a P. Il en résulte que le rapport P/n est constant quel que soit n. Il n’y a donc pas d’effet.

Þ Dans un système opérant à volume constant (système isochore) l’ajout d’un gaz inerte n’ a pas d’effet sur la réaction.

6.b Si le système opère à pression constante

Dans le cas de système isobare, trois cas se présentent.

6.2-a Si la molécularité ne change pas au cours de la réaction, si Dn = 0, lorsqu’on ajoute un gaz inerte, le rapport

(P/n)^Dn = 1 et il n’y a pas d’effet sur la réaction.

6.2-b Si Dn > 0, quand n croît, le précédent rapport décroît. Pour compenser cette décroissance et afin de respecter la constant d’équilibre, le rapport

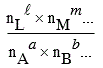
doit croître. Il doit donc y avoir déplacement d’équilibre vers la droite et donc une augmentation dans la formation des produits.

6.2-c Si Dn < 0, quand n croît, le rapport (P/n)^Dn croît.

Pour compenser cette croissance et afin de respecter la constante d’équilibre, le rapport

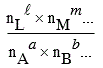
doit décroître. Il doit donc y avoir déplacement d’équilibre vers la gauche. En d’autres termes, il y a diminution dans la formation des produits.

7. Constante d’équilibre pour une réaction hétérogène

Ces réactions sont industriellement nombreuses et économiquement importantes. Elles incluent les réactions de décomposition d’oxydes, de carbonates, d’hydrates salins, ...

Soit la réaction

ZnO (s) + H₂ (g) ® Zn (s) + H₂O (g)

l’équation [7.3] s’écrit

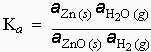
L’activité d’un solide pur ou d’un liquide pur est égale à l’unité jusqu’à de hautes pressions et pratiquement à toutes températures.

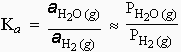On peut donc ignorer les solides et les liquides purs dans l’établissement de la constante d’équilibre.

Démonstration thermodynamique :

Soit la réaction

a A + b B + . . . ® L + m M + . . .

et supposons que les constituant A, B... L, M... se partagent en deux groupes :

a- des solides ou liquides purs distingués par l’indice i, et

b- des gaz parfaits distingués par l’indice j.

[7.20]

avec

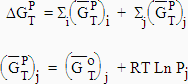Pour un solide ou un liquide pur, la variation de l’énergie libre avec la pression est négligeable. Donc,

[7.21]

Donc, [7.22]

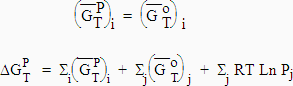À l’équilibre, la variation de l'énergie libre est nulle :

[7.23] Þ

Conclusion :

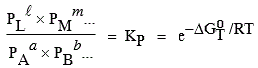
Dans l’expression de la constante K_P, on ne tient compte que des pressions partielles des composés gazeux. Par contre, dans l’expression de , tous les composants interviennent.

Exemple 1, oxydation du fer par l’eau. L’équilibre suivant gouverne le système :

3 Fe (s) + 4 H₂O (g) Fe₃O₄ (s) + 4 H₂ (g)

avec

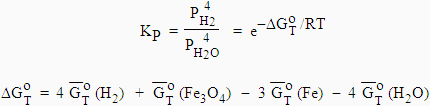On aurait pu écrire :

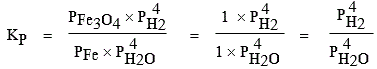
Il aurait alors fallu comprendre que dans la phase solide Fer, il n’y a que du fer et que sa pression hypothétique est de un (1) atmosphère ou encore, ce qui est plus juste, que son activité thermodynamique est égale à l’unité.

Exemple 2, carbonatation de la chaux vive :

Soit la réaction CaO (s) + CO₂ (g) ® CaCO₃ (s)

Au-dessus de la chaux vive, CaO, ajoutons graduellement du gaz carbonique. Tant et aussi longtemps que l’on n’a pas atteint la constante d’équilibre de décomposition du carbonate de calcium, P_CO₂, il ne se passe aucune réaction chimique. Dès que cette pression est atteinte, la réaction de carbonatation démarre et la pression de CO₂ demeure constante jusqu’au moment où toute la chaux vive a été transformée en carbonate de calcium. Pendant cette étape de carbonatation appliquons la règle de la variance :

u = C + 2 - j = 2 (3 constituants - 1 réaction chimique) + 2 (T et P) - 3 phases = 1.

Comme les deux solides ne sont pas solubles l’un dans l’autre, il faut compter trois phases. Si la réaction de carbonatation se fait à la température ordinaire, donc à une température donnée, la pression de gaz carbonique est fixée par le système. Elle l’est à travers la détermination de la constante d’équilibre de la réaction. Lorsque la chaux vive a disparu, le nombre de phases est réduit à deux, le système redevient bivariant et la pression de gaz carbonique peut augmenter.

Exemple 3, hydratation du sulfate de cuivre

Le système eau-sulfate de cuivre est soumis aux trois équilibres suivants :

[1] CuSO₄,H₂O ® CuSO₄ + H₂O; K_P = 0,8 mmHg,

[2] CuSO₄,3 H₂O ® CuSO₄,H₂O + 2 H₂O; K_P = (5,6 mmHg)²,

[3] CuSO₄,5 H₂O ® CuSO₄,3 H₂O + 2 H₂O; K_P = (7,8 mmHg)².

Figure 7.1. Variation de la pression durant l’hydratation
d’une mole de sulfate de cuivre anhydre.

On observera donc dans ce cas trois paliers de pression (Fig. 7.1). Ces paliers sont bien sûr déterminés par les constantes d’équilibre des réactions. En ajoutant, à 25 ºC, de la vapeur d’eau au-dessus du sulfate de cuivre anhydre, on atteint tout d’abord un plateau situé à 0,8 mmHg. La pression demeure stable jusqu’à transformation du sulfate anhydre en sulfate monohydraté. Puis la pression s’élève à nouveau jusque 5,6 mmHg où elle demeure stable jusqu’à transformation complète en sulfate dihydraté. On observe enfin un autre plateau de pression à 7,8 mmHg jusqu’à transformation complète en sulfate pentahydraté.

8. Variation de K_P et de K_a avec T - Équation de VAN'T HOFF

À l’équilibre, l’équation [7.5] s'écrit,

- RT Ln K_a

[7.24] Þ

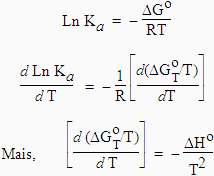voir l’équation [4.4]

[7.25] Þ

Dans le cas d’un gaz parfait, K_a = K_P

[7.26]

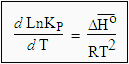C’est l’équation de VAN'T HOFF (1884).

Pour intégrer cette équation, il faut non seulement connaître la variation de l’enthalpie standard de réaction, DH^o, mais également les variations de DH^o avec la température : DH^o = ƒ(T). En considérant l’intervalle de température assez petit, on peut supposer que DH^o est constant.

[7.27]

[7.28] Þ

[7.29]

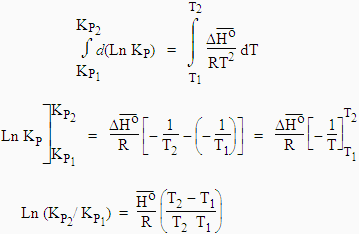Ou encore de façon plus générale, en introduisant les valeurs relatives à la température T₁ dans la constante d’intégration, on obtient :

[7.30]

[7.31]

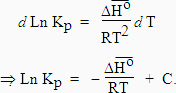Sur un graphe Ln Kp = ƒ(1/T), la pente sera égale à -/R et C est l’ordonnée à l’origine. Si varie sur l’intervalle de température. . . Les tables donnent les variations de capacité calorifique à pression constante, DCp, avec la température : voir Chapitre I.3. On obtient des formules de la forme

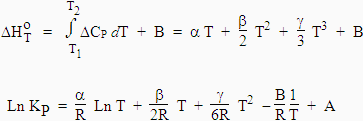Si la température T = 0,

= B.

Ceci n’est vrai qu’au zéro absolu où cette valeur est purement hypothétique. La constante B ne peut être confondu avec la variation d’enthalpie standard .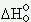

[7.32]

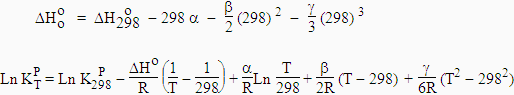Si DH^o est constant sur l’intervalle de température, on retrouve l’expression [7.29].

9. Autre forme de l’équation de VAN'T HOFF

On se souvient de l’équation [7.12],

[7.12] K_P = K_c (RT)^Dn

De plus, DH = DE + PDV avec PDV = Dn RT car (PV = n RT)

Ln K_C,T = Ln K_P,T - Dn Ln RT

[7.33]

[7.34]

[7.35]

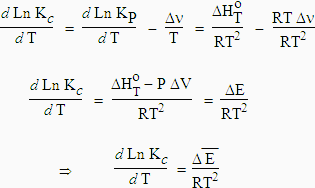La constante d'équilibre par rapport aux concentrations, K_c, joue par rapport à l'énergie interne le même rôle que la constante d'équilibre K_P par rapport à l'enthalpie (voir équation [7.26]).

10. Équilibres ne faisant intervenir que des phases condensées pures

(sans phase gazeuse, ni solutions liquides ou solides)

Dans ces cas,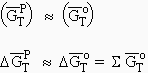
et quelle que soit la pression :

La condition d’équilibre se réduit à

Lorsqu’il y avait un gaz, il y avait possibilités d’équilibre à toute température avec P = ƒ(T). Dans le cas où le système ne fait intervenir que des phases condensées pures, il n’existe qu’une seule température (si cette température existe) à laquelle le

s’annule. À toute autre température, il y aura réaction complète, dans un sens ou l’autre.

Fe (s) + S (s) ® FeS (s)

11. Conclusions

Élément de référence important, la règle de la variance est donnée par la relation u = C + 2 - j. On détermine les constantes d’équilibre par rapport à l’activité de chacun des constituants d’un mélange. Pourvu que les coefficients d’activité sont voisins de l’unité, les constantes d’équilibre peuvent s’exprimer en termes des concentrations, des fractions molaires.

Lorsqu’un stress est imposé à un équilibre, la loi de LE CHATELIER - BRAUN permet de prévoir le sens de la modification de l’équilibre. L’ajout d’un gaz inerte est sans effet si la réaction a lieu à volume constant. Par contre, son effet à pression constante, dépend de la variation positive ou négative du nombre de moles observées au cours de la réaction.

Dans le cas d’une réaction hétérogène, l’activité d’une phase pure étant égale à l’unité, on ne tient compte que des pressions partielles (gaz) et des activités en solutions condensées.

Les constantes d’équilibre varient en fonction de la température. Par exemple, K_p est lié à l’enthalpie et K_C à l'énergie interne.

Pour en savoir un peu plus

Un site intéressant à consulter : http://www.edu.gov.mb.ca/m12/frpub/ped/sn/chimie_40s/docs/reg_4.pdf .

VAN T'HOFF : http://nobelprizes.com/nobel/chemistry/1901a.html

12. Exercices

12.1. Formation de l'iodure d'hydrogène

On observe l’équilibre de BODENSTEIN : I₂ + H₂ 2 HI. À 763,8 et à 666,8 K on obtient les constantes d’équilibre K_P : elles sont respectivement 60,80 et 45,62. Calculez la variation d’enthalpie de cette réaction (on négligera la variation de DH avec la température puisque DT < 100 ºC).

Réponse : DH = -12,5 kJ·mol^-1.

12.2. Réduction de la vapeur d'eau par le carbone

L’étude des réactions chimiques entre le carbone et le gaz carbonique montre les résultats suivants :

[1] C (s) + CO₂ (g) 2 CO (g) ; (équilibre de BOUDOUARD)

R T log K_P₁ = - 40 900 + 4,9 T log T - 4,95 10^-³ T² + 3,1 10^-⁷ T³ + 12,66 T

[2] CO₂ (g) + H₂ (g) CO (g) + H₂O (g)

R T log K_P₂ = - 10 100 + 1,81 T log T - 4,45 10^-³ T² + 4,8 10^-⁷ T³ + 0,54 T

[3] C (s) + H₂O (g) CO (g) + H₂ (g).

En utilisant le principe de l’état initial et de l’état final, déterminer la valeur de R T log K_P₃en fonction de la température T.

Réponse : RT log K_P3 = -30 800 + 3,09 T log T - 0,50 10^-3 T² - 1,7 10^-7 T³ + 12,126 T

12.3. Dissociation de PCl₅

Le pentachlorure de phosphores, PCl₅, se dissocie selon la réaction :

PCl₅ (g) PCl₃ (g) + Cl₂ (g)

a- À 250 °C, K_P = 1,78 atm. Trouvez la fraction a de PCl₅ qui est dissociée, si la réaction se déroule à la pression atmosphérique.

Réponse : a = 0,444

b- On recommence la même expérience mais cette fois dans un ballon fermé. Une mole de PCl₅ y est introduite sous une pression initiale de 1 atm. Calculez la pression finale ainsi que la faction a' de PCl₅ qui est dissocié.

Réponse : a' = 0,714

c- Cette décomposition est étudiée sous la pression atmosphérique et à 403 K. À cette température, le mélange obtenu à partir de PCl₅ pur a une densité de 4,80 g/dm³. Calculez le degré de dissociation a de PCl₅ et la valeur de DG à cette température. Recalculez la valeur de a si la pression totale est toujours de 1 atmosphère mais en présence d’une pression partielle d’argon de 0,5 atmosphères. Pouvez-vous réconcilier ces résultats et la loi de Lechatelier-Brown ?

12.4. Dissociation de l’anhydride sulfurique

Soit la réaction :

[2] 2 SO₃ (g) 2 SO₂ (g) + O₂ (g)

avec

= 183,1 kJ mol^-¹ et

= 132,9 kJ mol^-¹.

Quel serait le rendement (% d’anhydride sulfureux transformé en SO₃) de la réaction si on introduit un mélange comportant 8 % de SO₂, 10% d’oxygène et 82 % d’azote dans un réacteur opérant à 450 K et sous la pression atmosphérique?

Réponse : La réaction est complète.

12.5. Oxydation de l’argent métallique

Le problème de l’oxydation de l’argent métallique est bien connu des propriétaires de coutellerie argentée : ils doivent périodiquement nettoyer les ustensiles qui noircissent en se recouvrant d’oxyde d’argent. Existe-t-il des conditions de température propres à la conservation de l’argenterie. Soit donc l’équilibre :

Ag₂O (s) 2 Ag (s) + 1/2 O₂ (g)

On donne les valeurs suivantes :

Composé	Ag₂O (s)	Ag (s)	O₂ (g)
DH (kJ·mol^-¹)	- 30,56	0	0
DS^o (J·K^-¹·mol^-¹)	121,60	42,68	204,82

1- Calculer la pression de l’oxygène à 298 K à l’équilibre

La capacité calorifique des constituants de l’équilibre est donnée par la relation :

= a + b (10^-³) T + d (10⁺⁵) T^-² J·K^-¹·mol^-¹

Composé	Ag₂O (s)	Ag (s)	O₂ (g)
a	55,43	21,27	34,57
b	29,43	4,26	1,08
d	-	1,50	-7,86

Réponse : P_O₂ = 0,000 166 atm = 0,126 mmHg.

2- Calculer la valeur de DC_P(réaction) en fonction de la température T.

Réponse : DCp(réaction) = 4,39 - 20,37 10^-³ T - 0,93 10⁵ T^-²

3- Calculer la valeur de

en fonction de la température T.

4- En déduire les valeurs de DH^o à 100, 200, 300, 400, 500, 600 et 700 K.

5- Calculer la valeur de

en fonction de la température T.

6- En déduire les valeurs de DS^o à 100, 200, 300, 400, 500, 600 et 700 K.

7- En déduire les valeurs de DG^o à 100, 200, 300, 400, 500, 600 et 700 K.

8- En déduire la constante d’équilibre K_P à 100, 200, 300, 400, 500, 600 et 700 K.

Dire comment varie K_P avec l’augmentation de température.

9- Déterminer graphiquement la température d’équilibre lorsque l’argenterie est exposée à l’air?

Réponse : l’équilibre sera atteint vers 410 K, soit encore vers 137 °C.

Quelle conclusion en tirez-vous pour préserver l’argenterie de l’oxydation?

12.6. Procédé HABER

Soit la synthèse de l’ammoniac :

1/2 N₂ (g) + 3/2 H₂ (g) ® NH₃ (g)

On donne les valeurs de

(x) = a + b T 10^-³ + c T^-² 10⁵

x	a J·K^-1·mol^-¹	b J·K^-²·mol^-¹	d kJ·mol^-¹	kJ·mol^-¹	S J·K^-¹·mol^-¹
H₂	+ 27,28	+ 3,26	+ 0,50	-	130,59
N₂	+ 28,58	+ 3,76	- 0,50	-	191,5
NH₃	+ 29,75	+ 25,10	- 1,55	- 46,11	192,5

1- Calculer la valeur de

(réaction) .

Réponse : DH^o(réaction) = -46,11 kJ/mol.

2- Calculer

en fonction de la température T.

3- En déduire les valeurs de DH^o à 400, 450, 500 et 550 ºC.

Réponse : -54,104 kJ/mol à 550 °C.

4- Calculer la valeur de

de la réaction.

5- Calculer la valeur de

en fonction de la température T.

6- En déduire les valeurs de DS^o à 400, 450, 500 et 550 ºC.

Réponse : -116,4 J/mol/K à 550 °C.

7- En déduire les valeurs de DG^o à 400, 450, 500 et 550 ºC.

Réponse : + 41,49 kJ/mol à 550 °C.

8- En déduire la constante d’équilibre thermodynamique à 400, 450, 500 et 550 ºC sous une pression d'une (1) atmosphère. En déduire le sens de la variation de la constante K_P avec la température T.

Réponse : K_p= 0,002 33 (atm^-1) à 550 °C.

9- En supposant que les gaz ont un comportement idéal, établir la relation

en fonction de la pression P.

10- Calculer les valeurs de DG₄₅₀ sous des pressions de 10, 50, 100 et 300 atmosphères.

11- En déduire la constante thermodynamique à l’équilibre à 450 ºC et sous 10, 50, 100 et 300 atmosphères ainsi que les compositions des phases gazeuses à l’équilibre en supposant le mélange initial stœchiométrique. En déduire le sens de la variation de K_P quand la pression croît.

12- Aux pressions mentionnées la constante Kg = 0,99, 0,94, 0,88 et 0,69 sous les pressions respectives de 10, 50, 100 et 300 atmosphères. En déduire ce que devient le mélange stœchiométrique à ces pressions.

Réponse : à la pression de 300 atm et à 450 °C, 92 % du mélange sont transformés en ammoniac.

Voir un texte mi historique, mi scientifique relatif au procédé HABER : G. Emptoz, L'Actualité chimique, le journal de la Société chimique de France, La nouvelle chimie de l'azote dans l'entre-deux-guerres, N° 381, pages 40-46, (janvier 2014).

12.7. Équilibres entre sels et leurs hydrates

À 25 °C, les tensions de vapeur du système phosphate monoacide de sodium et l'eau, Na₂HPO₄ – H₂O sont les suivantes :

Équilibres		Pression de vapeur (Pa)
Na₂HPO₄,12H₂O	Na₂HPO₄,7H₂O + 7 H₂O	2550
Na₂HPO₄,7H₂O	Na₂HPO₄,2H₂O + 5 H₂O	1934
Na₂HPO₄,2H₂O	Na₂HPO₄ + 2 H₂O	1306

a- Sachant qu’à la température considérée, le phosphate bisodique anhydre et ses hydrates sont solides, en vous servant de la règle des phases, expliquez pourquoi la pression doit être constante lorsqu’il y a équilibre entre deux hydrates.

b- Qu’arrive-t-il si on augmente graduellement la pression au-delà de 2550 Pa?

c- Quel hydrate sera stable à l’air et à 25 °C si la pression partielle de la vapeur d’eau est de 1400 Pa?

12.8. Fabrication du carbure de molybdène

Quelle pression de méthane faut-il ajouter au-dessus du molybdène à 973 K pour obtenir une pression partielle d’hydrogène de 76 kPa? On donne la valeur de la constante d’équilibre pour la réaction suivante :

2 Mo (sol) + CH₄ (gaz)

Mo₂C (sol) + 2 H₂ (gaz);

Kp = 360 kPa

Réponse : 53 822 Pa.

12.9. Déshydratation du cuivre trihydraté

Soit la réaction de déshydratation suivante :

CuSO₄,3H₂O

CuSO₄,H₂O + 2 H₂O(gaz)

On observe que la pression de dissociation est de 746,8 Pa à 298,2 K et on sait par ailleurs que la variation de l’enthalpie sous la pression atmosphérique (101,333 kPa) et à 0 °C est de 112,86 kJ. On considérera cette valeur indépendante de la température.

Quelle sera la pression de dissociation à 100 °C ?

Quelle sera la température de dissociation sous une pression de 101333 Pa de vapeur d’eau ?

Réponse : T = 107 °C

Que pouvez-vous dire ou conclure de la température de dissociation dans l’air ambiant ?

12.10. Dissociation du dioxyde de carbone

À 3000 K et sous la pression atmosphérique (~101 333 Pa), 40 % du dioxyde de carbone est dissocié en monoxyde de carbone et en oxygène moléculaire. Quelle sera le degré de dissociation si la pression est élevée à 2 atmosphères ?

Réponse : le degré de dissociation du CO₂ à 3000 K sous 2 atm est 33,5 %.

Quel sera le degré de dissociation de CO₂ lorsqu’un mélange de 50 % de CO₂ et de 50 % de O₂ est porté à 3000 K sous la pression atmosphérique ?

12.11. Décomposition thermique du carbonate de calcium

Soit la réaction :

CaCO₃ (sol)

CaO (sol) + CO₂ (gaz)

On sait que pour cette réaction : DH_o° = + 182,875 et DG_o° = 134,763 kJ/mol.

- Calculez pour cette réaction : la valeur de DS_o°.

Réponse : DS_o° = 164,2 J/(mol·degré).

- En admettant que la valeur de l’enthalpie est indépendante de la température, calcules la valeur de DG_o°.

- On place 10 g de carbonate de calcium solide dans un récipient préalablement évacué à 800 K. Quelle sera la pression finale dans le réacteur.

Réponse : Kp(800) = 4,33 10^-4 Pa.

Dernière mise à jour : 2021-07-08.

x x x x x x x x x x x