|
Parmi les solutions, les solutions diluées, parce qu’elles sont diluées, minimisent les interactions entre molécules de soluté. Elles méritent donc une attention particulière. Questions : Objectifs :
|
1. Chaleur de formation d’une solution
On s’intéresse ici à la variation d’enthalpie qui accompagne la formation d’une solution tout particulièrement quand elle est diluée. Supposons que l’on dissolve une (1) mole d’un composé 2 (le soluté) dans n1 moles de composé 1 (le solvant). On constate que la chaleur de dissolution d’une mole de soluté,
![]()
dépend de la quantité n1 sauf pour de grandes valeurs de n1, donc en solution très diluée. Cette valeur tend donc vers une valeur
![]()
qui reste constante en solution suffisamment diluée :
|
|
est appelé la chaleur limite de dissolution. |
Tableau 9.1. Chaleur de dissolution de l’acide sulfurique H2SO4 (1 mole) dans n1 moles d’eau
n1 |
0,5 |
1 |
2 |
5 |
10 |
100 |
400 |
103 |
104 |
105 |
¥ |
|
15,26 |
23,86 |
41,9 |
66,3 |
67,0 |
73,9 |
76,2 |
78,5 |
87,0 |
93,5 |
96,1 |
Les valeurs sont exprimées en kJ. |
|||||||||||
2. Solubilité d'un gaz dans un liquide
D’après le Chapitre VII, la constante d’équilibre d’un constituant B présent dans deux phases en équilibre est telle que :
![]()
Pour une solution très diluée en B, l’activité aB(liq) peut être changée par la fraction molaire, xB, et la phase gazeuse pouvant être considérée idéale,
| [9.1] | K = PB / xB | avec aB(liq) = xB . |
La loi de HENRY :
|
Nota : la loi de RAOULT (voir Chapitre VIII.6) n’est valable que pour le solvant et la loi de HENRY n’est valable que pour le soluté (Fig. 9.1).
Figure 9.1. Domaines d’application
respective des lois de HENRY et de RAOULT
pour la substance B
(diagramme isotherme).
3. Solution idéale d’un solide dans un liquide
Soit une solution de naphtalène (B) dans du benzène (A). Soit xB,s la fraction molaire de naphtalène dans la solution saturée. xB,s représente donc la solubilité du naphtalène dans le benzène. Supposons aussi qu’il existe en équilibre avec la solution saturée des cristaux de naphtalène pur. À l’équilibre thermodynamique l’énergie libre du naphtalène est la même dans les deux phases. Donc,
|
[9.2] |
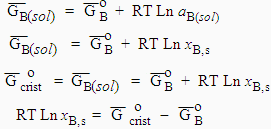 |
et si la solution est idéale et Donc,
|
Le produit RT Ln xB,s est constant à une température donnée. Les propriétés du solvant A n’apparaissent pas dans cette dernière équation. La valeur de xB,s est donc indépendante de la nature du solvant. Cette valeur doit donc être identique pour n’importe quel solvant pourvu que la solution demeure idéale. Le tableau 9.2 montre une série de ces valeurs pour le naphtalène dans divers solvants. Les valeurs xB,s sont voisines de 0,3 pour ce soluté. On voit le cas de la solution d'hexane qui s'écarte grandement de l'idéalité.
Tableau 9.2. Valeur de xB,s pour le naphtalène dans divers solvants
Solvant |
CHCl3 |
C6H5Cl |
CH2=CHCl |
pyridine |
C6H5NO2 |
C6H6 |
xB,s |
0,331 |
0,317 |
0,317 |
0,314 |
0,298 |
0,296 |
Solvant |
C6H5CH3 |
mais |
hexane : |
la solution n’est plus idéale! | ||
xB,s |
0,286 |
0,125 |
||||
Effet de la température sur la solubilité
La dernière équation peut se réécrire de la façon suivante [9.2]):
|
[9.3] |
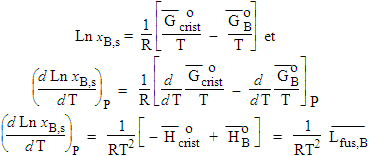 |
Dans cette relation
![]()
est la chaleur latente molaire de fusion du composé B à la température de la solution. Si la température de la solution est proche de la température de fusion normale du composé B, T ~ TB, cette valeur peut être confondue avec
![]()
au point de fusion normale TB. D’où, pour T ~ TB, la formule de SCHRÖDER - VAN LAAR :
| [9.4] |
|
Soit un soluté mis en solution dans un système de deux solvants non miscibles. Le soluté se distribue dans les deux solvants A et B où il atteindra les concentrations respectives CA et CB. Dans chacun des deux solvants l’énergie libre partielle molale du soluté atteindra une valeur telle que :
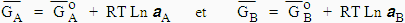
| À l’équilibre : [9.5] |
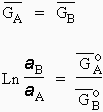 |
ou, si la solution est suffisamment diluée,
Ln CB / CA = constante
![]()
[9.6] ou encore K = CB / CA dans une solution diluée.
La lettre K représente le coefficient de partage. Le tableau 9.3 montre quelques-unes des valeurs de K.
Tableau 9.3. Exemple de distribution d’un soluté entre deux solvants immiscibles
Soluté |
Solvant A |
Solvant B |
K* |
Iode |
CCl4 |
Eau |
85 |
SO2 |
Eau |
CHCl3 |
1 |
HgCl2 |
Eau |
Benzène |
12 |
| * K = [soluté](solvant A) / [soluté](solvant B). | |||
Application à la distribution d’un composé dissociable dans l’une des phases
Soit à étudier la distribution de l’acide benzoïque entre l’eau et le benzène. Dans l’eau l’acide benzoïque se dissocie en ions H+ et C6H5COO- mais, compte tenu du faible coefficient de dissociation, on peut ignorer cette réaction. Par contre, dans le benzène, l’acide benzoïque s’associe avec lui-même :
C6H5COOH ![]() C6H5COO- + H+
C6H5COO- + H+
n C6H5COOH
![]() (C6H5COOH)n
(C6H5COOH)n
Soit a le coefficient d’association. La loi de distribution s’applique aux molécules non transformées. Si C1 et C2 sont les concentrations totales respectives d’acide benzoïque libre ou lié présent dans l’eau et le benzène :
![]()
Selon le tableau de bilan appliqué en phase organique (C2 est la concentration d’acide benzoïque libre et lié) :
Molécules |
C6H5COOH |
(C6H5COOH)n |
Total |
Avant |
C2 |
0 |
C2 |
À l’équilibre |
(1 - a) C2 |
a/n C2 |
C2 |
Si k est la constante d’équilibre de la réaction d’association, alors :

En combinant ces deux équations, il vient :
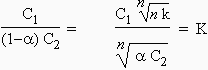
Dans ce cas l’association est pratiquement complète et puisque
![]()
est une constante à température fixe, on peut écrire :
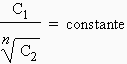
On mesure, en fonction de la quantité d’acide benzoïque ajoutée au mélange eau - benzène, les valeurs de C1 et de C2. On calcule ensuite les valeurs
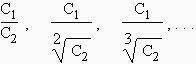
On trouve que le rapport est constant avec n = 2. L’acide benzoïque s’associe par paire de molécules dans le benzène : (C6H5COOH)2 . Ceci n’est valable que si les solutions sont diluées. Sinon, les activités doivent remplacer les concentrations.
Applications industrielles
En milieu industriel, l’extraction, solvant - solvant est fréquente. Afin de contrecarrer la limite d’extraction imposée par le coefficient de distribution, on utilise très fréquemment la technique du contre-courant qui permet l’extraction totale (voir Chapitre X.5).
5. Propriétés des solutions diluées
Les trois propriétés qui suivent font partie de ce que l’on appelle les propriétés extensives, (en anglais : colligative properties) qui dépendent donc de la quantité de matière, par opposition aux propriétés intensives qui, elles, n’en dépendent pas. Par exemple, l’indice de réfraction, la densité, la couleur... sont des propriétés intensives alors que la masse, le volume... sont des propriétés extensives.
|
|
Figure 9.2. Abaissement de la courbe de pression.
5.a L’ébulliométrie
Il s’agit de la conséquence de l’abaissement de la pression de vapeur du solvant par introduction d’un soluté : on observe l’augmentation de la température d’ébullition (Fig. 9.2). La loi de RAOULT est telle que (cas d’une solution idéale) :
P = Po xA avec xA < 1 Þ P < Po.
La pression de vapeur du solvant est donc inférieure à sa pression de vapeur saturante Po et la décroissance est fonction (proportionnelle) à la fraction molaire du solvant. Si le soluté est non volatil, il ne contribue pas à la pression P.
Þ DP = Po - P = Po (1 - xA) = Po xB
La diminution de pression ne dépend que de la fraction molaire du soluté et de la pression de vapeur saturante du solvant.
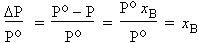
L’abaissement relatif ne dépend que de xB, donc de la nature seule de B. La loi de CLAUSIUS-CLAPEYRON (forme intégrée de l’équation de CLAPEYRON : voir Chapitre VI.2) peut être utilisée pour le solvant :
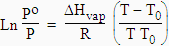
Dans cette équation
P et Po sont les pressions de vapeur saturante aux températures T et To et DHvap est la chaleur latente de vaporisation au voisinage de la température T.
|
car T est voisin de T0 . |
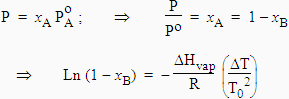
Note : le signe négatif du membre de droite de cette dernière équation s’accorde avec la valeur absolue de DT.
Quand la concentration de B tend vers zéro, xB ® 0, en développant en série on obtient :
![]()
En négligeant les termes supérieurs, Ln (1 - xB) tend vers - xB quand xB tend vers 0.
| [9.7] Þ |
|
En substituant la molalité m (nombre de moles par 1000 g de solvant), à la
fraction molaire

[9.8] DT = Kéb m
La constante Kéb ne dépend que du solvant : c’est la constante ébullioscopique du solvant. Cette propriété est utilisée pour calculer m donc pour calculer la masse molaire d’un soluté. Le tableau 9.4 montre quelques valeurs de la constante ébullioscopique.
Tableau 9.4. Constantes ébullioscopiques de quelques solvants
Solvant |
Température |
Kéb
(observés) |
Acétone |
56,5 |
1,72 |
Tétrachlorure de carbone |
76,8 |
5,0 |
Benzène |
80,1 |
2,57 |
Chloroforme |
61,2 |
3,88 |
|
Éthanol |
78,4 | 1,20 |
Éther diéthylique |
34,6 |
2,11 |
Méthanol |
64,7 |
0,80 |
Eau |
100,0 |
0,51 |
Source : Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, MacMillan Co, New York, 1967. |
||
|
|
Figure 9.3. Abaissement du point de fusion.
Appliquons la loi de CLAUSIUS-CLAPEYRON successivement à la courbe de vaporisation et de sublimation (Fig. 9.3) :
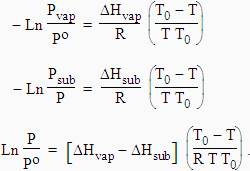 |
|
|
et |
|
|
Þ |
Comme DHvap + DHfus = DHsub
![]()
Si la loi de RAOULT est à nouveau applicable, le raisonnement utilisé précédemment conduit à :
| [9.9] |
|
Kf est la constante cryoscopique du solvant.
NOTA : dans le cas des électrolytes, les valeurs DTfus, DTvap, DPvap et DP (voir plus loin, paragraphe 5.) sont plus grandes. Si la constante cryoscopique de l’eau est de 1,85, avec HCl, HNO3, NH4Cl, ... la valeur mesurée est le double. VAN'T HOFF a suggéré que le rapport
![]()
Ou encore DTfus = n Kf m où n est le nombre d’ions libérés par le soluté (voir la théorie de dissociation électrolytique d’ARRHENIUS, 1887). Le tableau 9.5 montre quelques valeurs de la constante cryoscopique.
Tableau 9.5. Constante cryoscopique de quelques solvants
Solvant |
Température |
Kfus
(observés) |
Acide acétique |
16,7 |
3,9 |
Bromoforme |
7,8 |
14,4 |
Benzène |
5,5 |
5,12 |
Phénol |
42 |
7,27 |
Cyclohexane |
112 |
20,3 |
Camphre |
178,4 |
37,7 |
Eau |
0,00 |
1,86 |
|
Source : Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, MacMillan Co, New York, 1967. |
||
5.c L’osmométrie
|
|
Figure 9.4. Principe de fonctionnement de l’osmomètre.
Soit un récipient séparé par une cloison semi-perméable en deux compartiments (Fig. 9.4). Dans le premier, introduisons un solvant A pur en équilibre avec sa pression de vapeur saturante Po. Dans le second compartiment, introduisons le même solvant et un soluté B. Cette solution est en équilibre avec la pression PA du solvant. La cloison est dite semi-perméable puisqu’elle permet le libre passage des molécules de solvant d’un compartiment vers l’autre. Par contre elle ne permet pas le transfert de molécules de soluté. À l’équilibre l’énergie libre molaire du solvant dans chacun des deux compartiments devrait être la même :
![]()
puisque
![]()
Si l’on accroît la pression du solvant, PA, d’une quantité dPA, G2 varie de
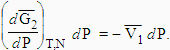
|
|
est le volume partiel molaire du solvant dans la solution. |
|
La variation de la pression de |
|
entraîne : |
|
À l’équilibre,
Þ |
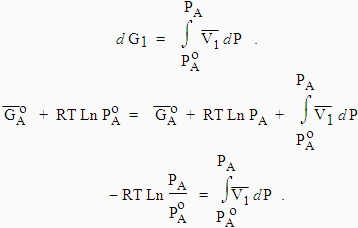 |
L’intervalle de pression est petit
![]()
et comme de plus les liquides peuvent être considérés incompressibles (le volume molaire est constant),
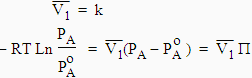
| [9.10] Þ ou encore |
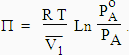 |
Le symbole
P représente la pression osmotique. Comme|
|
= Ln (1 - xB) et que ce logarithme tend vers - xB quand xB tend vers 0. |
| [9.11] |
Þ xB R T = |
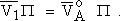 |
| Comme de plus
|
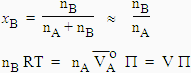 |
pour une solution diluée, où V est le volume du solvant. |
La loi de VAN'T HOFF pour une solution idéale se traduit par :
| [9.12] | P = (nB / V) RT = c RT |
La grandeur c représente la molarité (nombre de moles/litre) du constituant B. Attention aux unités : si P est en atmosphères, l'utilisation du système « litre atmosphère » peut être judicieuse ! Le tableau 9.6 montre les valeurs observées et calculées dans le cas du sucrose. Il permet aussi de voir qu'avec une molalité de 1,0 la solution est déjà loin de l'idéalité.
Tableau 9.6. Comparaison entre les valeurs observées et calculées de la pression
osmotique
d’une solution de sucrose à 30 ° C
m |
P observé |
P calculé |
|
(atm) |
[9.10] |
[9.12] |
|
0,10 1,0 2,0 3,0 4,0 5,0 6,0 |
2,47 27,22 58,37 95,16 138,96 187,3 232,3 |
2,44 27,0 58,5 96,2 138,5 183,0 231,0 |
2,40 20,4 35,1 45,5 55,7 64,5 - |
Source : Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, MacMillan Co, New York, 1967. |
|||
Lorsque c devient trop grand, la pression osmotique prend la forme :
[9.13] P = R T c (1 + b cn).
L’osmométrie présente plusieurs avantages.
[9.14]
|
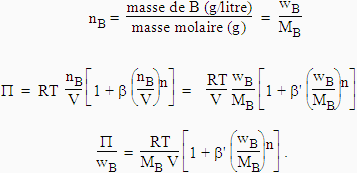 |
Le rapport
P/wB est appelé la pression osmotique réduite : elle est fonction de wB. Si n = 1, cas assez fréquent,| [9.15] |
|
et lorsque wB tend vers 0, le rapport
![]()
Sur le diagramme P = ƒ(wB), le rapport R T / (MB V) est l’ordonnée à l’origine.
Cette méthode est intéressante car, même si MB est grand (cas d’un polymère) la pression osmotique P est encore mesurable. On peut en effet mesurer convenablement P même avec des masses de 1000 à 10 000 alors que la cryométrie et l’ébulliométrie sont limitées à des masses molaires inférieures à 200.
Exemple : cas des solutions sanguines.
On observe que l’abaissement cryoscopique est de 0,56 ºC.
| [9.16] |
|
La pression osmotique est telle que :
P = c R T = R T (n/V) = 0,0812
(273 + 37) 0,30 = 7,55 atm.En soins infirmiers, cette pression osmotique est importante. Les cellules qui se trouvent dans le flux sanguin sont en équilibre avec cette pression. Pour ce faire, les solutions se trouvant à l’intérieure de la cellule ont des solutés à la même pression osmotique (Fig. 9.5 A). Si l’on injecte de l’eau pure à un patient (solution hypotonique), soudainement la pression osmotique chute et les cellules sont soumises à une pression interne. Pour contrer ce déséquilibre, les cellules doivent soit permettre aux solutés de quitter la cellule ou d’absorber des molécules d’eau. Ce dernier mécanisme est le plus rapide de telle sorte que la cellule enfle (Fig. 9.5 B). C’est le phénomène de turgescence. Éventuellement, si le déséquilibre est trop grand, la cellule peut éclater. Au contraire si l’on injecte une solution de pression osmotique plus grande que la pression osmotique du sang (solution hypertonique), on observera le mécanisme inverse et, par perte de molécules d’eau, la molécule se recroqueville : c’est le phénomène de plasmolyse (Fig. 9.5 C).
En général, on injecte à des patients des solutions qui contiennent » 0,91 % de NaCl pour être isotoniques du sang.
|
|
Figure 9.5.
Effet
des concentrations relatives en soluté entre l’intérieur et l’extérieur
de la cellule
:
A : cellule dans un milieu contenant un soluté en concentration CA;
B : cellule dans un milieu contenant un soluté en concentration CB < CA;
C : cellule dans un milieu contenant un soluté en concentration CC > CA.
|
|
Figure 9.6. Principe de fonctionnement détaillé de l’osmomètre.
|
Les solutions diluées sont gouvernées par la loi de RAOULT qui s’applique au solvant et par la loi de HENRY qui s’applique au soluté. Diverses autres lois sont aussi applicables. La relation entre la température et la solubilité d’un soluté dans un solvant suit la loi de SCHRÖDER – VAN LAAR dans certaines limites. La loi de NERST s’applique au coefficient de partage d’un soluté entre deux solvants non miscibles. Les propriétés importantes des solutions diluées concernent la cryoscopie, l’ébulliométrie et l’osmométrie. Ces propriétés sont utilisées pour mesurer la masse molaire de divers solutés (molécules simples, dissociables et polymères).
|
7.1. Calculez la pression de vapeur à 25 °C d’une solution qui contient 0,400 moles de sucre dans 500 g d’eau. La pression de la vapeur saturante de l’eau à 25 °C est de 23,5 mmHg.
Réponse : P(solution) = 23,16 mmHg.
7.2.
Trouvez le point de congélation d’une solution qui contient 0,2 moles d’un soluté non dissocié dans 1 200 g de benzène. Le point de congélation du benzène est de 5,5 °C ?Réponse : Tfus(solution) = 4,65 °C.
7.3. Une solution aqueuse contient 5 % en poids d’urée CH4N2O et 10 % en poids de glucose C6H12O6. Quel sera son point de congélation?
Réponse : T = - 2,58 ºC.
7.4. Une solution aqueuse d’urée (0,013 m) montre une diminution de la température de congélation de 0,024 o. Quel serait l’abaissement correspondant pour une solution aqueuse de même concentration de chlorure de sodium NaCl ?, de sulfate de potassium, K2SO4 ?
Réponse : DTfus(NaCl) = 0,048 °C.
7.5. 2,441 g d’acide benzoïque abaissent de 0,2048 °C le point de fusion de 250 g de benzène. Quelle est la forme moléculaire de l’acide benzoïque dans ce solvant dont on précise que la constante cryoscopique est de 5,12 º·m-1 ?
Réponse : l’acide benzoïque se trouve à l’état de dimère dans la solution.
7.6. Un échantillon non volatil est dissout dans du chloroforme. Cette solution montre une élévation du point d’ébullition de 3,00 °C sous une pression de 1 atm. En supposant que la solution est idéale, calculez la fraction molaire du soluté. On indique que la constante ébulliométrique du chloroforme est de 3,88.
Réponse : xB = 0,089.
7.7 La pression osmotique d’une solution aqueuse contenant 45 g de sucrose C12H21O11 par litre de solution est de 2,97 atm à 0 ºC. Trouvez la constante des gaz et comparez-la avec la valeur acceptée.
Réponse : R = 8,384 J / (° · mol) en SI.
7.8. La pression osmotique du sang humain est de 7,7 atm à 40 ºC. Quelle est la concentration probable des solutés dans le sang ? En supposant que cette concentration est essentiellement la même que la molalité, trouvez le point de congélation du sang.
7.9
Réponse : P = 0,00492 atm = 3,74 mmHg.
7.10. Déterminez le poids moléculaire d’une substance qui produit une pression osmotique de 40,8 mm d’une colonne d’eau à 25 °C. On précise que 10 g du soluté ont été dissout dans 1000 ml de solution. Faire le calcul d’erreur permettant de préciser l’incertitude sur le poids moléculaire trouvé.
Réponse : M = 62 kg/mol et DMB / MB ~ 11 %.
7.11. Une solution de 3,795 g de soufre dans 100 g de bisulfure de carbone, CS2, - Tébul = 46,30 °C - bout à 46,66 °C. Quelle est la formule de la molécule de soufre dans ce solvant ? La constante ébullioscopique du est de 2,50 °C/mole de soluté / kg de solvant.
Réponse : La formule est S8.
7.12. On utilise la cryoscopie pour étudier la structure de l’acide acétique dans le benzène [Peterson, J. M. et W. H. Rodebush, J. Phys. Chem., 32, 709 (1928)]. Le tableau suivant donne la quantité d’acide acétique en fonction de l’abaissement du point de fusion de la solution. Quel est le degré d’association de l’acide acétique dans le benzène ? La constante cryoscopique du benzène est de 5,1 º·m-1.
On donne : n CH3COOH ® (CH3COOH)n
Masse d’acide (g) dans 1000 g de C6H6 |
DT (°C) |
Masse d’acide (g) dans 1000 g de C6H6 |
DT (°C) |
0,201 0,399 0,845 2,894 5,802 |
0,0156 0,0277 0,0539 0,1472 0,253 |
14,25 30,57 62,44 97,56 148,86 |
0,608 1,254 2,410 3,644 5,202 |
Tracez la courbe Masse moléculaire apparente / masse moléculaire de l’acide acétique en fonction de la molalité de cet acide.
7.13. Pour déterminer la constante cryoscopique de l’eau, on réalise les expériences correspondantes aux résultats affichés dans le tableau suivant :
m (molalité du soluté) |
0,000 538 |
0,004 235 |
0,007 645 |
0,012 918 |
0,018 87 |
0,030 84 |
0,042 48 |
DTfus |
0,001 00 |
0,007 85 |
0,014 13 |
0,0240 |
0,0350 |
0,0570 |
0,0785 |
Calculez pour chacune des 7 expériences la constante cryoscopique Kf. Évaluez la précision sur cette mesure.
Réponse : l’acide acétique s’associe sous la forme de dimère.
__________________________
Dernière mise à jour : 2021-07-09.
x x x x x x x x x x x x x x x x