|
|
|
Après avoir vu la diversité et la complexité des systèmes binaires, on peut soupçonner la plus grande diversité et complexité des systèmes ternaires. La représentation en même temps sur une figure des concentrations de 3 constituants et de la variable température ajoute à la difficulté. Que deviennent les courbes de solidus et de liquidus ? Quelles sont les principales applications industrielles de ces diagrammes ? |
1. Généralités
De nombreux diagrammes ont été étudiés en particulier ceux des alliages métalliques. Les diagrammes mettant en jeu deux sels et l’eau sont aussi très importants puisqu’ils sont la source de nombreuses applications industrielles. La représentation plane n’est plus adéquate puisqu’en plus de trois composants il faudra pouvoir "visualiser" l’effet de la température. Il faut donc faire appel à une représentation spatiale.
1.b La règle des phases
La relation de la variance u établie au Chapitre VII.2 garde toute sa valeur :
u = C + 2 - j. Comme C = 3, j £ 5.
En fait, le plus souvent le paramètre pression sera exclus (diagrammes de phases condensées). Donc j £ 4. Il faut donc disposer d’une représentation ayant au moins trois dimensions : par exemple deux concentrations et la température.
|
|
Figure 12.1. Représentation d’un système à trois composés à température fixe.
Sur la figure 12.1 on a proposé une solution dans un solvant A de deux solutés B et C. L’axe horizontal représente le pourcentage de B et l’axe vertical celui de C. Le quadrilatère ALMN représente le domaine de la solution de B et C dans A. C’est donc une région à une phase ou encore une région monophasée. Le segment MN représente le lieu des points représentant la solution saturée en B. Le quadrilatère non complété BNMP représente la région d’équilibre entre la solution saturée en B et probablement une phase b riche en B. La région PMQ représente une région d’équilibre à trois phases : la solution saturée à la fois en B et en C, la phase b et la phase g. En admettant que la pression n’est pas un paramètre (les phases sont toutes des phases condensées), dans ces régions la variance est :
- zone ALMN : u = 3 + 1 (T) - j = 4 - 1 = 3;on détermine la température et deux compositions;
- zone BNMP : u = 3 + 1 (T) - j = 4 - 2 = 2, c’est-à-dire le facteur T additionné d'une concentration;
- zone PMQ : u = 3 + 1 (T) - j = 4 - 3 = 1, c’est-à-dire le facteur T.
La composition de chaque phase est déterminée à chaque température et le point M est déterminé par le système. La position de M ne peut varier que si la température T varie. Si l’on veut représenter la variation que le facteur T entraîne sur ce système, il faut faire appel à une représentation spatiale (Fig. 12.2).
|
|
Figure 12.2. Représentation spatiale d’un système ternaire.
La courbe L'L" représente le lieu des solutions binaires AB, saturées en B. Le segment curviligne M'M" représente les solutions ternaires saturées à la fois en B et en C avec variation de la température.
1.c Application du théorème des moments chimiques
Ce théorème démontré pour le cas des systèmes binaires (voir Chapitre VIII.10) s’applique toujours aux régions des diagrammes ternaires dans lesquelles deux phases sont en équilibre. Les masses des deux phases en équilibre sont proportionnelles aux portions opposées du segment conjugué MN (Fig. 12.3). Dans les régions du diagramme où coexistent trois phases, u = 3 + 1 - 3 = 1. Si la température est fixée, la variance devient nulle et la composition des phases en présence est déterminée quelle que soit la composition du mélange initial. Seule la proportion relative de chacune des phases varie en fonction de la composition globale. Le théorème des moments chimiques peut alors être étendu aux trois dimensions (Fig. 12.4) :
![]()
|
|
Figure 12.3. Théorème des moments chimiques (région à 2 phases).
|
|
Figure 12.4. Théorème des moments chimiques (région à 3 phases).
1.d Systèmes de représentations triangulaires
Méthode de ROOZEBOOM :
A B Figures 12.5. Représentations triangulaires.
La figure 12.5A représente la représentation originale de ROOZEBOOM. Soit un point L. Par ce point traçons les trois parallèles aux trois côtés du triangle équilatéral. Le principe de cette représentation repose sur le fait que la somme des segments LM + LN + LP = AB. Par définition on pose :
|
- masse de A = wA = a
LM = a
Ba |

|
où a est un coefficient de proportionnalité.
Donc, si Ba représente la concentration de A, tous les mélanges ayant cette concentration se trouvent sur le segment aP et ainsi sur chacun des trois côtés. Cette représentation, quoique très judicieuse, oblige à établir le sens des graduations des pourcentages. La figure 12.5A a retenu le sens trigonométrique inverse (les sens des aiguilles d’une montre). On aurait très bien pu "polariser" le triangle en sens contraire. Ce mode de représentation force donc à un effort particulier de lecture.
Il existe une autre façon plus commode de lire ce diagramme. En effet, si d’un point intérieur L (Fig. 12.5B) on élève les trois hauteurs relatives à chacun des côtés, les segments LM, LN et LP, la somme LM + LN + LP = AH quelle que soit la position du point L. Par définition on pose :
|
- masse de A = wA = b LM |
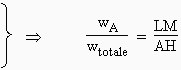 |
Notons que les deux modes de représentation conduisent à la même position du point L pour un mélange de composition donnée. La représentation en est cependant plus symétrique puisqu’il n’est plus nécessaire d’indiquer comment est "polarisé" le triangle. On trouve d’ailleurs dans le commerce des diagrammes préparés dans l’esprit de cette représentation.
Quoiqu’il en soit, dans chacune des deux approches, un mélange ne contenant pas de A se trouve représenté par un point du côté BC.
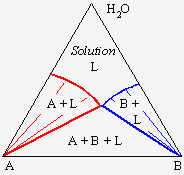
2. Systèmes liquide-liquide
Un exemple de ce type de mélange apparaît à la figure 12.6. Le système eau-chloroforme-acide acétique peut se décomposer en trois diagrammes binaires :
- un système eau-acide acétique où les deux liquides sont miscibles en toutes proportions;
- un système chloroforme-acide acétique où les deux liquides sont miscibles en toutes proportions;
- un système eau-chloroforme où les deux liquides sont partiellement miscibles.
|
|
Figure 12.6. Diagramme isotherme eau-chloroforme-acide acétique.
À l’intérieur du triangle, dans le système ternaire apparaît une zone où le liquide se sépare en deux phases : une phase organique et une phase aqueuse. Cette zone d’équilibre à deux phases est délimitée par une binodale marquant la saturation des deux phases liquides. Par exemple, un mélange représenté par le point L se séparera en deux phases. Les liquides de compositions M et M' seront en équilibres et le segment MM' est un segment conjugué. En augmentant la concentration en acide acétique, le point L se déplacera en direction du point A et le segment MM' deviendra NN', puis PP', pour éventuellement se terminer en R, le point critique de la binodale. En augmentant la température du mélange, la solubilité réciproque de l’eau et du chloroforme augmente et la zone à deux phases diminue d’importance (Fig. 12.7). Éventuellement on atteindra une température à laquelle on obtiendra une solubilité totale des trois composés quelle que soit la composition du mélange.
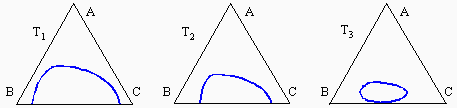
Figures 12.7. Effet de la température sur le diagramme eau-chloroforme-acide acétique :
T1 < T2 < T3 < T4 < T5.
|
|
Figure 12.8. Diagramme eau-phénol-acétone.
|
|
Figure 12.9. Diagramme eau-phénol-aniline.
Les figures 12.8 et 12.9 sont du même type. Si la solubilité de l’aniline dans le phénol est bonne et inversement, la solubilité de ces deux composés organiques dans l’eau est faible, tout au moins à 50 ºC. On a porté en pointillé sur chacun de ces deux diagrammes le lieu des points critiques des binodales de saturation. Remarquons aussi que l’on a porté la température maximum où l’on observe deux phases : 92 et 168 ºC. Si l’on essaie de visualiser à quoi peuvent ressembler ces deux diagrammes en fonction de la température, on verra rapidement se dessiner dans chaque cas une sorte de colline : les courbes d’égales températures jouant le rôle de ligne de niveau sur une carte d’État-major.
Pour ceux intéressés par l'histoire de la chimie, on trouvera une application fort intelligente de l'utilisation des propriétés du sytème ternaire liquide-liquide eau-éthanol-pentanol. En 1876, le physico-chimiste Émile Jacques Duclaux (1840-1904) a construit un thermomètre à minima pour des utilisations particulières. Description et fonctionnement à découvrir dans la revue de la Société chimique de France, L'Actualité chimique, Nº 446, 52-56 (décembre 2019).
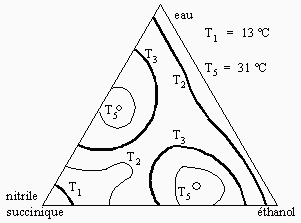 |
Figure 12.10. Système eau-éthanol-nitrile succinique.
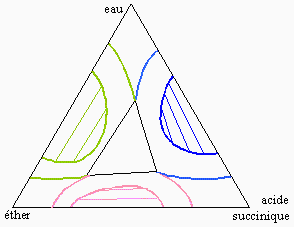 |
Figure 12.11. Système eau-éther-acide succinique.
La figure 12.10 représente un système de trois liquides dont deux sont complètement miscibles et les deux autres paires sont partiellement miscibles formant éventuellement deux binodales de saturation, binodales « culminant » ou se terminant par une solubilité complète à des températures supérieures à 31 ºC. En fonction de la température on aura en quelque sorte deux monts.
La figure 12.11 représente un système où chacune des paires de liquides est peu miscible, formant ainsi trois binodales de saturation.
3. Étude du liquidus - système Pb-Bi-Sn
|
|
Figure 12.12. Diagramme ternaire plomb - bismuth - étain
(Pascal, Tome XX-2, 1913,1860).
|
|
Figure 12.13. Projection des courbes de liquidus du diagramme Pb-Bi-Sn
Les courbes sont les isothermes des surfaces
de liquidus: les chiffres sont les températures en °C.
La composition en poids du mélange eutectique ternaire fondant à 96 ºC est tel que :
Pb (36 %), Bi (52,5 %) et Sn (15,5 %). C’est l’alliage de DARCET (ou D’ARCET).
Voir aussi :
- Pb-Sn-Cd (21,04-57,02-21,90 % atom.) fondant à 145 ºC,
- Bi-Sn-Cd (39,3-33,2-27,5 % atom.) fondant à 104 ºC,
- Bi-Pb-Cd (48,21-37,72-24,07 % atom.) fondant à 91,5 ºC.
- LiF-KF-NaF fondant à 492 ºC.
Exemples de cas types :
A
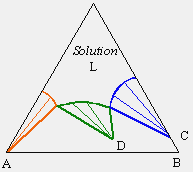
KCl-NaCl-H2O, les points A et B représentent les sels insolubles l’un dans l’autre.
B
NaCl-Na2SO4-H2O à 15 ºC
sels mutuellement insolubles l’un dans l’autre; formation d’un sel hydraté au point C :
(point C º Na2SO4·10H2O).
C
NH4NO3-AgNO3-H2O, sels mutuellement insolubles; formation d’un intermédiaire : (le point A,B représente le sel double NH4NO3,AgNO3).
D
KNO3-AgNO3-H2O, sels mutuellement insolubles; formation d’un intermédiaire :
(A,B º KNO3,AgNO3).
Figures 12.14. Représentation de quelques cas types de diagrammes ternaires.
Le système NH4NO3-AgNO3-H2O permet la cristallisation congruente du sel double tandis que le système KNO3-AgNO3-H2O est incongruent. On peut en effet montrer qu’à partir d’un mélange équimoléculaire des sels A et B on peut obtenir quantitativement le sel double A,B. La position du sel double KNO3-AgNO3-H2O est à l’extérieur du segment IJ obtenu en alignant le sommet du diagramme et les extrémités de la binodale de saturation de ce sel double. On peut ici montrer qu’à partir d’un mélange équimoléculaire des sels A et B on ne peut obtenir quantitativement le sel double A,B. On peut remarquer l’effet de la température sur le diagramme CaCl2-MgCl2-H2O (Fig. 11.14E et F).
E
CaCl2-MgCl2-H2O, à 25 ºC. On observe la formation d’un sel ternaire : point D º CaCl2,MgCl2·12H2O.
F
CaCl2-MgCl2-H2O. Formation de sels hydratés insolubles mutuellement CaCl2·6H2O et MgCl2·6H2O.
G
(NH4)2SO4-K2SO4-H2O à 25 ºC, sels complètement miscibles.
H
NH4Cl-FeCl2-H2O à 70 ºC, A et B,H2O sont miscibles, (B,H2O º FeCl2·2H2O).
Figures 12.14 (suite). Représentation de quelques cas types de diagrammes ternaires.
On remarque sur les figures 11.14G, H et I la solubilité mutuelle de pairs de sels, soit entre les sels anhydres (Fig. 12.14G), un sel anhydre et un sel hydraté -cas moins fréquent- (Fig. 12.14H), soit deux sels hydratés (Fig. 12.14I).
I
(NH4)Cr(SO4)2-(NH4)Fe(SO4)2-H2O, à 25 ºC, A,H2O et B,H2O miscibles.
J
KCl-KI-H2O à 25 ºC, sels partiellement miscibles.
K
MnCl2-CoCl2-H2O à 15-20 ºC, Sels hydratés partiellement miscibles : MnCl2·4H2O et CoCl2·6H2O.
L
Na2SO4-NaBrO3-H2O, Sels hydratés partiellement miscibles : série de sels intermédiaires à 45 ºC.
Figures 12.14 (fin). Représentation de quelques cas types de diagrammes ternaires.
4. Quelques exemples de diagrammes ternaires
4.a Séparation du mélange Pb-Ag à l’aide du zinc
La métallurgie du plomb produit le plus souvent un mélange très pauvre en argent (titre inférieur à 2,6 %). Par refroidissement d’un tel mélange on obtient du plomb puis un eutectique contenant 2,6 % argent (température de fusion de l’eutectique » 300 ºC) (Fig. 12.15). Ce procédé d’obtention de l’eutectique est appelé le pattinsonage : il n’est guère usité car si le plomb contient au départ 2 % d’argent, l’enrichissement en ce métal est très limité. On préfère employer le zincage.
Le zincage
Le zinc est peu soluble dans le plomb, au moins jusqu’à 700 ºC (Fig. 12.16). Par contre l’argent se dissout beaucoup plus facilement dans le zinc que dans le plomb. Il se forme même des composés intermédiaires du type Ag2Zn5, Ag2Zn3, AgZn et Ag2Zn. La couche superficielle qui contient la majorité de l’argent, contient un peu de plomb. Elle est chauffée au rouge et y injecte de la vapeur d’eau. Celle-ci oxyde le zinc en ZnO. On sépare alors facilement les scories contenant cet oxyde. La phase liquide restante est essentiellement constituée de plomb et d’argent : point Q du diagramme. On peut maintenant refroidir ce mélange : il précipitera l’argent métallique pur et l’on arrêtera au moment de l’apparition des premiers cristaux d’eutectique argent-plomb. L’argent métallique est séparé et le liquide proche de la composition eutectique est recyclé, de telle sorte que tout l’argent peut être extrait et que le coût en zinc est maintenu au minimum.
|
|
Figure 12.15. Diagramme binaire Pb-Ag.
|
|
Figure 12.16. Diagramme binaire Pb-Zn.
Figure 12.17. Diagramme ternaire Pb-Ag-Zn à 650 ºC
(réf. : Pascal, tome XX,2, 1923).
Le diagramme Au-Ag-Cu est aussi de ce type.
4.b La métallurgie de l’aluminium
La préparation de l’aluminium par électrolyse de l’alumine fondue est facilitée par l’addition de fluorine, CaF2 et de cryolithe, Na3AlF6. En effet, l’alumine ne fond qu’à plus de 2000 ºC, rendant coûteux son électrolyse ignée. Par contre, les diagrammes binaires alumine-fluor et alumine-cryolithe donnent lieu à deux diagrammes avec formation d’un eutectique dont les températures de fusion respectives sont de 1270 et 904 ºC. Le diagramme ternaire quant à lui indique la formation d’un eutectique ternaire fondant à 867 ºC et dont la composition est la suivante :
cryolithe : 59,3 % fluorine : 23 % et alumine : 17,7 %.
En fait, d’autres additifs tel que le trifluorure d’aluminium, la fluorine, permettent de travailler vers 800 ºC, diminuant d’autant les coûts de chauffage (fusion de l’alumine). Le diagramme binaire NaF-AlF3 (la cryolithe Na2NaAlF6) montre la présence de divers composés intermédiaires (Na5Al3F14) ce qui permet de travailler avec des conditions de fluidité de bain de fusion très convenable.
|
|
Figure 12.18. Diagramme ternaire Al2O3-CaF2-Na3AlF6
(Les températures sont exprimées en °C).
|
|
Figure 12.19. Diagramme ternaire Al2O3-CaF2-Na3AlF6
ainsi que ses trois diagrammes binaires (en °C).
4.c Le cas des ciments - fabrication du ciment Portland
Le système CaO-SiO2-Al2O3 est bien évidemment important. Le ciment Portland a été inventé par un anglais, J. ASPDIN en 1824. Il contient divers oxydes de fer, magnésium, ... On peut cependant le considérer essentiellement constitué des trois oxydes d’aluminium, de calcium et de silicium.
Le système binaire SiO2-Al2O3 montre la présence :
- d’un eutectique dont la température de fusion est de 1545 ºC, ainsi que
- d’un composé intermédiaire, Al6Si2O13, ou encore 3 Al2O3,2 SiO2, qui a un point de fusion incongruent à 1810 ºC.
Le système binaire SiO2-CaO montre la présence de trois composés intermédiaires :
- CaSiO3 dont la température de fusion est de 1540 ºC,
- Ca3Si2O7 dont la température de fusion est de 2130 ºC, ainsi que
- Ca2SiO4 (ou encore 2 CaO,SiO2).
Il se forme trois eutectiques dont les températures de fusion sont : 1436, 1550 et 2065 ºC. Il existe aussi une zone d’équilibre entre deux liquides au-dessus de 1700 ºC. Enfin, un composé Ca3SiO5 n’existe pas en équilibre avec le liquide.
Le système binaire CaO-Al2O3 montre la présence d’au moins quatre solides en équilibre avec le liquide ainsi que quatre eutectiques (Tableau 12.1).
Tableau 12.1. Principaux éléments du système CaO-Al2O3
Composés |
Ca3Al2O6 |
Ca5Al6O14 |
CaAl2O4 |
Ca3Al10O18 |
Tfus (ºC) |
? |
1455 |
1600 |
1720 |
Eutectiques |
1455 |
1400 |
1590 |
1700 |
Deux composés ternaires stables à leur point de fusion ont été obtenus. Ce sont :
l’anorthite CaAl2Si2O8 dont la température de fusion est
de 1550 ºC et le Ca2Al2SiO7 dont la température de
fusion est de 1590 ºC. Le ciment Portland est un mélange de Ca3SiO5,
Ca2SiO4 et de Ca3Al2O6 avec un peu
de Ca5Al6O14, c’est-à-dire un mélange obtenu avec les
températures les plus basses obtenues sur les courbes de liquidus : Tmin
» 1335 ºC. En
fait la température d’obtention du ciment est plutôt située entre 1335 et 1500 ºC.
Comme les cinétiques de réactions d’échange en phase solide sont plutôt lentes, on
obtient un mélange qui n’est pas complètement à l’équilibre (voir
plus loin, la figure 12.24.)..
4.d Des notions de minéralogie
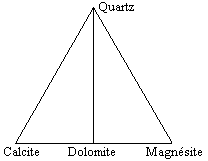
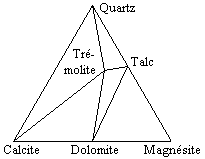
À la température normale (TPN) le diagramme quaternaire SiO2-CaO-MgO-CO2 représenté sous la forme ternaire SiO2-CaCO3-MgCO3, apparaît à la figure 12.20. Le quartz, la calcite, la dolomite et la magnésite sont les composés stables. Dans des conditions un peu plus élevées (Fig. 12.21),
- par exemple : 200 < T (ºC) < 300 et P = 1 bar, ou encore
300 < T (ºC) < 400 et P = 2000 bars, ou encore
350 < T (ºC) < 400 et P = 2000 à 10 000 bars
le talc et la trémolite deviennent stables.
5 CaMg(CO3)2 + 8 SiO2 + H2O ® |
Ca2Mg5Si8O22(OH)2 + 3 CaCO3 + 7 CO2 |
(dolomite) |
|
|
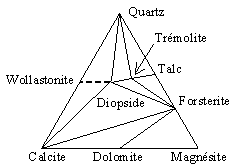
| Figure 12.20. | Figure 12.21. |
|
|
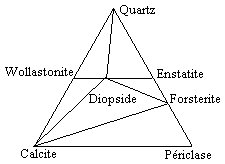
| Figure 12.22. | Figure 12.23. |
Dans des conditions de température plus sévères :
- par exemple : 300 < T (ºC) < 500 et P = 1 bar, ou encore
400 < T (ºC) < 700 et P = 2000 bars,
la diopside et la forstérite, Mg2SiO4, deviennent stables (Fig. 12.22).
Ca2Mg5Si8O22(OH)2 + 3 CaCO3 + 2 SiO2 ® |
5 CaMgSi2O6 + 3 CO2 + H2O |
(trémolite) |
(diopside) |
Si l’on continue à augmenter les conditions extérieures :
-par exemple : 500 < T (ºC) < 700 et P = 1 bar, ou encore
700 < T ºC < 1000 et P = 4000 bars,
la wollastonite CaSiO3, le périclase, MgO, et l’enstatite, Mg2Si2O6, deviennent stables alors que la dolomite et le talc ne le sont plus (Fig. 12.23). Le diagramme ternaire CaO-Al2O3-SiO2 (le diagramme de la céramique) montrant les courbes de liquidus simplifiées apparaît à la figure 12.24. On y retrouve plusieurs composés (minerais) que l’on retrouve dans la région Saguenay-Lac Saint-Jean tels que l’anorthite, CaAl2Si2O8, (Shipshaw, Québec), la wollastonite (Saint-Ludger-de-Millot, Québec). Par ailleurs, le diagramme K2O-Al2O3-SiO2 indique la position de plusieurs composés chimiques stables intermédiaires. On y trouve également les points représentatifs de certaines productions de l’activité économique humaine, comme la porcelaine « Médicis », ou les poteries de grès « Thaï » et celles du de la région rhénane (Fig. 12.25).
|
|
Figure 12.24. Diagramme CaO-Al2O3-SiO2.
Légende :
| Cr : cristobalite, SiO2 | Tr : tridymite, SiO2 |
| Wo : wollastonite, CaSiO3 | Ge : gehlenite, Ca2Al(AlSiO7) |
| An : anorthite, Ca(Al2Si2O8) | Co : corundum, Al2O3 |
| Mu : mullite, Al6Si2O13 |
|
|
Figure 12.25. Diagramme K2O-Al2O3-SiO2.
Légende :
| A : 3 Al2O3,2SiO2 | F : K2O,SiO2 |
| B : K2O,Al2O3 | G : K2O,4SiO2 |
| C : K2O,Al2O3,2SiO2 | X : porcelaine « Médicis » |
| D : K2O,Al2O3,4SiO2 | Y : poterie de grès « Thaï » |
| E : K2O,Al2O3,6SiO2 | Z : poterie de la région rhénane |
L’ensemble de ces résultats appliqués en minéralogie permettent d’estimer les conditions de température et de pression (profondeur dans le sol) qui ont prévalu lors de la formation de ces dépôts. Évidemment ces données sont imprécises car les systèmes impliquant des transformations en phase solide ont des cinétiques de conversion très lentes. D’autre part le système CO2-H2O à hautes pressions et à hautes températures n’est pas facile à manipuler. En outre les données représentées sont bien évidemment incomplètes : d’autres intermédiaires sont possibles et surtout d’autres éléments viennent compliquer un portrait déjà trop simplifié. Enfin, l’analyse chimique précise de produits industriels ou d’artefacts archéologiques permet d’en identifier l’origine géographique ou industrielle.
Il est intéressant
d’introduire ici une variante importante qui donne lieu à la formation de "verres".
En effet, la silice comme plusieurs autres oxydes de métalloïdes (B2O3, GeO2, P2O5, As2O5 et
As2O3) donne lieu à la formation de verres
qui peuvent également inclure en proportions diverses des oxydes alcalins,
alcalino-terreux et métalliques. Le
principe physique de formation est simple : il repose sur la vitesse de
refroidissement du mélange en fusion.
Un refroidissement suffisamment lent permet l’édification d’un réseau
périodique tridimensionnel d’atomes.
Il se forme alors de véritables cristaux.
Par contre un refroidissement rapide ne le permet pas.
Le solide ainsi formé garde « a mémoire » du désordre tridimensionnel
existant en phase liquide. Par
exemple, au lieu de former des
structures très variées mais bien connues sous forme de feuillets ou
d’autres ensembles organisés, les tétraèdres de SiO4-- se lient
au hasard avec leurs voisins.
L’agencement atomique est alors moins compact et le volume spécifique des verres
est plus grand que celui des cristaux correspondants (Fig.
12.26).
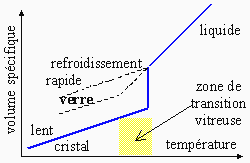
Figure 12.26.
Formation d’une phase cristalline ou vitreuse à partir d’un liquide.
4.e Cas des mélanges de paires énantiomères en solution
Le mélange solvant/M-(+)/M-(-) se traite évidemment bien avec la représentation triangulaire. On distinguera pour simplifier deux cas : celui du conglomérat et celui du mélange racémique. Le premier cas, le conglomérat, à température fixe, apparaît à la figure 12.27. On y distingue :
- la région SaEb correspond au domaine de la solution insaturée;
- sur le segment aE la solution est saturée en énantiomère A;
- sur le segment Eb la solution est saturée en énantiomère B;
- le point E représente la composition de l’eutectique;
- la région aEA est le domaine d’équilibre entre l’énantiomère A et sa solution saturée;
- la région bEB est le domaine d’équilibre entre l’énantiomère B et sa solution saturée;
- la région AEB est la zone d’équilibre entre la solution saturée en racémique et les deux énantiomères formant le conglomérat de composition globale variable.
Notons :
1- La position centrale du point E (mélange (+)/(-) = 50/50). Ce point se déplace sur la droite SR en fonction de la température T (se déplace vers R quand T croît);
2- Les segments Sa et Sb sont de longueurs voisines sinon égales;
3- Les segments aE et bE sont proches de la linéarité;
4- Les deux énantiomères ayant un comportement indépendant l’un de l’autre, la composition de la solution saturée en E contient deux fois plus d’énantiomères que chacune des deux solutions saturées en un seul énantiomère : points a et b.
Conséquences :
Un conglomérat de composition 50/50 ne pourra être séparé en ses deux énantiomères purs. Par contre un conglomérat de composition non équimoléculaire pourra être séparé en énantiomère pur (celui qui se trouve en majorité) et un mélange 50/50.
|
|
Figure 12.27. Diagramme ternaire d’un conglomérat en présence de solvant. |
Figure 12.28. Diagramme ternaire d’un mélange racémique en présence de solvant. |
Si la ligne brisée aEb de la figure 12.27 pouvait avoir une certaine analogie avec la courbe de liquidus du système eutectique déjà remarqué dans le cas du conglomérat, la ligne brisée de la figure 12.28 présente davantage de similitude avec la courbe de liquidus avec formation d’un intermédiaire (Fig. 12.18). Il existe enfin des cas où la solubilité en fonction de la température montre la présence d’un conglomérat dans une région de température et la présence du racémique dans une autre région de température (en dessous ou en dessus) (Fig. 12.29). Finalement, il existe aussi des diagrammes pour les pseudo-racémiques qui sont de peu d’utilité pour la séparation des énantiomères.
|
|
Figure 12.29. Diagramme d’un mélange où le conglomérat (histidine)
devient racémique à 45 > T > 25 °C.
5. Systèmes non-symétriques contenant de l’eau
5.a Représentation triangulaire
La représentation du diagramme apparaît à la figure 12.30. L’origine du diagramme, point O, représente l’eau pure. Le point A représente le sel anhydre A pur et le point B représente le sel anhydre B pur. Un point M situé à l’intérieur du triangle OAB représente un mélange ternaire eau-A-B. Dans ce triangle, il faut remarquer que la somme des segments aM + bM + dM est constante et on peut attribuer à cette somme 100 % :
aM + bM + dM = OA = OB
- le segment aM représentera le pourcentage de A,
- le segment bM représentera le pourcentage de B et
- le segment dM représentera le pourcentage d’eau.
|
|
Figure 12.30. Représentation triangulaire non symétrique.
En effet, si ce point M se trouve sur le côté OA, le segment bM = 0 et le point M est bien inclus dans le système binaire eau-A. Il en est de même sur le côté OB : le segment aM est nul et le pourcentage de A est nul. Sur l’hypoténuse AB, le segment dM est nul et le mélange est un mélange anhydre des sels A et B.
- Un sel double anhydre AmBn se trouve sur l’hypoténuse AB.
- Un sel hydraté Am,H2O se trouve sur le côté OA.
- Un sel double hydraté, AmBn,H2O, se trouve à l’intérieur du triangle OAB.
Il reste bien sûr à déterminer la zone de solubilité des sels ou encore la binodale de saturation de la solution.
5.b Séparation de la carnallite
Exemple d’un cas de solubilité non-congruente : la carnallite : KMgCl3·6H2O
|
|
Figure 12.31. Diagramme partiel H2O-MgCl-KCl.
Le diagramme ternaire apparaît en figure 12.31. La région délimitée par le pentagone curviligne OPDEQ détermine la région ne contenant qu’une seule phase : la solution aqueuse. La courbe PD détermine la binodale de saturation de la solution en chlorure de magnésium hexahydraté. Celle DE en fait autant pour le sel double hydraté KMgCl3·6H2O, la carnallite et la courbe EQ détermine la solution saturée en KCl. Le triangle curviligne BPD détermine une région à deux phases où la solution saturée en MgCl2·6H2O est en équilibre avec ce sel. Le triangle BDC représente la zone d’équilibre entre trois phases : MgCl2, KCl·6H2O, MgCl2·6H2O et leur solution saturée...
Si l’on ajoute de la carnallite à l’eau de manière à obtenir une solution complète, le point représentatif du mélange se déplace sur le segment CO. Arrêtons la dissolution au point M et procédons à une évaporation isotherme. Le point représentatif du mélange va refaire le chemin inverse. Arrivé en N, le KCl commence à déposer. La solution s’appauvrissant en KCl, son point représentatif se déplace sur QE en direction de E pendant que se poursuit la cristallisation de KCl. Parvenu en N', si l’on n’arrête pas là l’évaporation, la carnallite va aussi cristalliser. On doit donc arrêter l’évaporation et séparer les cristaux de KCl par filtration.
Les borax sont des composés chimiques de formule générale xB2O5,yNa2O·zH2O : tableau suivant. Le diagramme ternaire H2O-B2O5-Na2O est intéressant sur le plan industriel mais également sur le plan pédagogique (Fig. 12.32). Il faut en effet réaliser que sur ce diagramme les composés BO2Na·1/2H2O et BO2Na·2H2O sont situés sur une droite passant par le point O représentatif de l’eau pure. De la même manière les points représentatifs de BO2Na·1/2H2O et BO3HNa2 sont sur une droite passant par le Na2O. En effet, ces deux composés peuvent aussi s’écrire : BO2Na·1/2H2O + B2O4H2·Na2O et BO3HNa2 + B2O4H2·2Na2O. Le minéral le plus abondant est la tincalconite : B4O7Na2·5H2O, le borax naturel en est une forme hydratée B4O7Na2·10H2O. Le tableau 12.1 résume tous ces éléments.
Tableau 12.1. Composés dérivés de formule xB2O5,yNa2O,zH2O
Composés |
x |
y |
z |
BO3H3 |
1 |
- |
3 |
B5O8Na·5H2O |
5 |
1 |
10 |
B4O7Na2·5H2O |
4 |
2 |
10 |
BO2Na·2H2O |
1 |
1 |
4 |
BO2Na·1/2H2O |
1 |
1 |
1 |
BO3HNa2 |
1 |
2 |
1 |
NaOH·H2O |
0 |
1 |
3 |
5.d Méthode des résidus humides - méthode de SCHREINEMAKERS
Les régions d’équilibre à deux phases ne sont pas toujours faciles à déterminer. La méthode des résidus humides proposée par SCHREINEMAKERS en est une qui permet de préciser la position de la binodale correspondant à la solution saturée ainsi que la composition du sel en équilibre avec cette solution saturée (Fig. 12.33). Un mélange de composition connue R' se sépare en une solution saturée S' et une phase solide C. Un autre mélange R" se sépare une solution saturée S" et une même phase solide C. La connaissance des compositions R' et R" d’une part et des compositions S' et S" d’autre part suffit à calculer la composition du point C. Il faut noter que si l’on connaît les masses de R' et de R", il n’est pas toujours facile de connaître la masse exacte des solutions S' et S". Dans le cas contraire, le théorème des moments chimiques peut être d’une aide précieuse.
|
|
Figure 12.32. Diagramme partiel des composés de l’acide borique et de la soude.
|
|
Figure 12.33. Méthode des résidus humides.
|
|
Figure 12.34. Représentation d’un cas d’isomorphisme.
Ce cas se rencontre lorsque les deux solides ont une structure semblable et sont solubles l’un dans l’autre sur toute l’échelle des concentrations (Fig. 12.34). Le diagramme de phase eau-sel A-sel B se réduit donc à une région de solution aqueuse avec une binodale délimitant la région de saturation et une région à deux phases montrant l’équilibre entre la solution saturée et la solution saline solide. Le segment conjugué NL montre qu’un mélange de composition M se sépare en deux phases. La première est une solution saturée (point N) en équilibre avec un solide cristallin de composition indiquée par le point L. C’est le cas du mélange
MnSO4·5H2O-CuSO4·5H2O-H2O à T > 10 ºC .
Le sel apparaissant sur l’hypoténuse AB a la formule : (Cu,Mn)SO4·5H2O. (Voir aussi Fig. 12.14G).
Ici les deux sels ne sont plus semblables. Ils sont cependant solubles l’un dans l’autre dans un domaine relativement important de concentration (Fig. 12.35). Entre ces deux zones de solubilité, on trouve une lacune de miscibilité. C’est le cas du mélange
MnSO4·7H2O-CuSO4·5H2O-H2O à température inférieure à 10 ºC .
Nota : le point B représente le sulfate de manganèse heptahydraté et le point A celui du sulfate de cuivre pentahydraté. Dans ce cas les coordonnées des points (x,y) et (x',y') sont les suivantes :
(x,y) : (3 %,9,5 %) et (x',y') : (8 %,8 %)
Il s’ensuit que le MnSO4·7H2O peut dissoudre jusqu’à 3 % de CuSO4·5H2O sous la forme de CuSO4·7H2O formant ainsi un sel double de formule (Mn,Cu)SO4·7H2O. De son côté le CuSO4·5H2O peut dissoudre jusqu’à 8 % de MnSO4·7H2O sous la forme de MnSO4·5H2O pour former un sel double (Cu,Mn)SO4·5H2O. L’hypoténuse observée dans le cas de l’isomorphisme s’est décomposée en deux morceaux non co-linéaires. (Voir aussi la figure 12.14K pour une autre forme de représentation).
|
|
Figure 12.35. Représentation d’un cas d’isodimorphisme.
5.g Effet de la température - séparation de la sylvinite NaCl,KCl
En représentation isotherme, le mélange KCl-NaCl est situé sur l’hypoténuse du triangle rectangle (Fig. 12.36). La région OPDQ délimite la région de la solution non saturée en NaCl et en KCl. Puisque DQ représente la solution saturée en KCl, le triangle AQD représente la région d’équilibre entre la solution saturée en KCl et le KCl solide. La zone BDA délimite la région d’équilibre entre une phase aqueuse saturée à la fois en NaCl et en KCl et chacun des deux sels anhydres. Le point M représente ainsi un mélange de solution saturée de masse wsol, et de sels de masse wNaCl et wKCl. En appliquant le théorème des moments chimiques, on obtient :
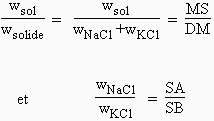
|
|
Figure 12.36. Diagramme d’équilibre de la sylvinite.
Si l’on ajoute de l’eau à un mélange de sels anhydres représenté par le point L", le point représentatif du mélange se déplace sur le segment OL" en direction de O. Si au contraire on opère une évaporation isotherme sur une solution représenté par le point H, ce point se déplace vers L".
Pour séparer les deux sels, on utilise la variation de solubilité avec la température (Fig. 12.37). On part en A avec une solution titrant 14 g de KCl et 20 g de NaCl dans 100 g d’eau. On évapore à 100 ºC. En B, le chlorure de sodium cristallise. On continue l’évaporation. Puisque la solution s’épuise en NaCl, le point représentatif de la solution se déplace de B vers C. À ce point, on sépare (filtration) le NaCl et l’on refroidit la solution à 0 ºC. La solution entre alors dans la zone de cristallisation du KCl : il précipite. Le titre en NaCl restant constant le point représentatif de la solution se déplace sur une horizontale, vers D. Arrivé en ce point, on chauffe à 100 ºC. En évaporant, le point représentatif de cette solution se déplace vers E, ... puis vers C, ... Il s’agit d’introduire à l’endroit approprié le mélange initial pour travailler en continue, c’est-à-dire en récoltant 100 % du KCl et du NaCl. Le cycle le plus efficace et le plus économique correspond à la séquence FBCF...
|
|
Figure 12.37. Effet de la température sur le diagramme ternaire
eau-KCl-NaCl
(poids de NaCl en g par 100 g d’eau = ƒ(poids de KCl par 100 g
d’eau).
5.h Le contrôle de la pureté
5.i Distillation d’un système ternaire - préparation de l’éthanol absolu
1ère étape : rectification de moûts fermentés
Le mélange eau-éthanol est un cas d’azéotrope avec température de distillation de l’azéotrope : T = 78,15 ºC. La matière première est constituée en général sur le plan industriel par des jus de fermentation contenant environ 10 ± 5 % d’éthanol. Par rectification (distillation sur colonne à plateaux) on obtient, en haut de colonne, le mélange azéotropique contenant approximativement 95 % d’éthanol. Dans la cuve, en bas de la colonne, on obtient éventuellement l’eau pure. Il est donc impossible d’obtenir l’éthanol pur par rectification de moûts fermentés. Pour résoudre ce problème, on utilise les propriétés du système ternaire eau-éthanol-benzène.
2e étape : distillation du système ternaire eau-éthanol-benzène (Fig. 12.38)
Au mélange azéotropique eau-éthanol (point A du diagramme ternaire), on ajoute du benzène pour obtenir un mélange de composition représentée par le point B. On distille ce mélange. Il produit, en haut de colonne un azéotrope ternaire dont la température d’ébullition est de 64,9 ºC et dont la composition est : eau (7,4 %), benzène (74,4 %) et éthanol (18,5 %). Il reste dans la cuve un mélange éthanol-benzène exempt d’eau (point D).
|
|
Figure 12.38. Diagramme ternaire eau-éthanol-benzène.
3e étape : rectification du système éthanol-benzène
Ce mélange éthanol-benzène est soumis à la rectification. Le système binaire éthanol-benzène donne lieu à une distillation azéotropique. Cette fois la composition du mélange est située du bon côté de la composition azéotropique : la rectification produit en haut de colonne, à une température de 67,8 ºC, un mélange azéotropique contenant de l’éthanol à 32,4 %. En bas de colonne, on récolte de l’éthanol pur. Il faut ajouter que l’éthanol obtenu, aussi pur soit-il, contient toujours des traces de benzène, le rendant par le fait même impropre à la consommation humaine.
4e étape : optimisation du procédé : limitations des pertes
Ce système laisse présager des pertes d’éthanol sous la forme d’azéotrope ternaire et sous la forme d’azéotrope éthanol-benzène ainsi que des pertes correspondantes en benzène. À partir du diagramme, on peut voir qu’on peut substituer le mélange azéotropique éthanol-benzène au benzène pur avant de procéder à la deuxième étape. On limite ainsi les pertes d’éthanol et de benzène. On ne peut malheureusement, sur les seules propriétés du diagramme ternaire, récupérer les pertes sous la forme d’azéotrope ternaire sans l’intervention d’une autre substance. Une possibilité de solution est d’ajouter à l’azéotrope ternaire un déshydratant (desséchant). Cette opération permettra de récupérer un mélange binaire éthanol-benzène voisin de sa composition azéotropique, donc recyclable. Le facteur coût fait évidemment partie des considérations industrielles.
6. Conclusions Comme on pouvait le prévoir, chaque cas de mélange ternaire est un cas particulier. On utilise la présentation isotherme triangulaire : - symétrique - triangle équilatéral (méthode de ROOZEBOOM), ou - dissymétrique - triangle rectangle (cas des solutions). Les courbes de liquidus, de solidus deviennent des surfaces. Le théorème des moments chimiques s’applique en deux dimensions. La métallurgie de l’aluminium, l’extraction de l’argent des minerais de plomb, les ciments, … font largement appel à la compréhension des diagrammes ternaires. |
7.1. Complétez le diagramme suivant en :
- identifiant ce que peut être la formule chimique du composé représenté par le point C;
- expliquant à quoi correspondent les segments curvilignes MP et PN;
- en expliquant ce que représente le segment AS;
- en indiquant les espèces en équilibre dans chaque région (on supposera que A et B sont mutuellement insolubles l’un dans l’autre).
7.2. Un mélange ternaire A-B-C, figure suivante, montre les caractéristiques suivantes :
1- A, B et C sont totalement insolubles l’un dans l’autre à l’état solide;
2- A, B et C sont totalement solubles l’un dans l’autre à l’état liquide; et
3- A, B et C forment deux à deux des systèmes eutectiques.
Dites comment évolue un mélange de composition indiquée par le point par le point L et porté à une température de 1 000 ºC. Dites comment se comporte la composition de la phase liquide pendant le refroidissement.
Note: les températures sont exprimées en °C.
Même question pour le mélange représenté par le point M.
Dans chacun des deux cas, tracez une courbe de refroidissement en y indiquant les températures des points particuliers.
Pour en savoir plus
Campbell, A. N. et N. O. Smith , The Phase Rule and its Applications, Dover Publ. inc., New York, 9e édit., 1951, 495 pages.
Frye, K., Modern Mineralogy, Prentice-Hall, inc., Englewood Cliffs, New Jersey, 1974.
Mark Pollard, A. et Carl. Heron, Archaeological Chemistry, The Royal Society of Chemistry, London, England, 1996.
On trouvera une excellente présentation (composition, propriétés, mise en forme, ...) sur les principaux verres disponibles sur le marché (borosilicates, fluosilicates, vitrocéramiques, ...) : C. Pierlot, A. Facqueur, M.-N. Maillet, F. Rochepeau et O. Rahimi, Bon repas ne va pas sans bonne vaisselle - Formulation et traitements de surface des verres des arts de la table, L'actualité chimique, 370, 8-14 (janvier 2013).
On trouvera sur le web de nombreux exemples de diagrammes de phase.
Également, un excellent site pour voir de très beaux spécimens de cristaux : https://www.mindat.org/ (visité le 2019-02-02).
Les propriétés du sytème ternaire liquide-liquide eau-éthanol-pentanol : Jérôme Andrieux et Françoise Khantine-Langlois, L'Actualité chimique, Nº 446, 52-56 (décembre 2019).
Dernière mise à jour : 2021-07-09.
x x x x x x x x x