|
|
relative au composé A pur, et |
|
|
relative au composé B pur |
LA THERMODYNAMIQUE DES SOLUTIONS
|
Objectifs Après avoir défini en général les fonctions thermodynamiques et quelques-unes de leurs propriétés, il est intéressant d’en faire l’application aux solutions. Questions :
Objectifs :
|
1. Rappels de quelques propriétés
Une solution de deux liquides miscibles en toutes proportions à la température T est dite idéale :
1- si sa vapeur peut être considérée comme un mélange de gaz parfaits. À l’équilibre, l’énergie libre par mole de mélange (ou encore le potentiel chimique de chaque constituant) doit être la même dans les deux phases.
2- si la pression de vapeur totale de la solution varie linéairement de la valeur
|
|
relative au composé A pur, et |
|
|
relative au composé B pur |
en fonction des fractions molaires dans la solution liquide.
Il est bien entendu que certaines solutions ne sont idéales que si elles sont diluées, c’est-à-dire dans une zone limitée de concentration du soluté.
Expression des unités de concentrations :
a) La plus rationnelle est la fraction molaire. Si n1 moles de solvant contiennent n2 moles de soluté, les fractions molaires du solvant x1 et du soluté x2 sont respectivement :
![]()
ou, d’une façon plus générale :
xj = nj / Si ni
L'intérêt de cette expression de la composition tient au fait qu'elle est sans dimension : elle n'a pas d'unités. Elle représente, au facteur 100 près, le pourcentage du nombre de molécules.
b) La molalité m est commode en solution diluée : c’est le nombre de moles d’un corps dissout dans 1000 g de solvant. Ainsi la molalité de l’eau pure est voisine de 55. La masse de solvant ne varie pas lorsqu'on ajoute le soluté. Si l’on dissout n2 moles d’un soluté de masse molaire M2 (g) dans un nombre n1 de moles de solvant de masse molaire M1, on aura :
![]()
c) La molarité c est le nombre de moles d’un corps dissout par litre de solution. De la même manière la molalité de l’eau pure est voisine de 55. Cette unité a le désavantage de varier avec la température puisque le volume varie avec la température. Par contre, la masse de solvant ne varie pas lorsqu'on ajoute le soluté. Si l’on dissout n2 moles d’un soluté de masse molaire M2 (g) dans un volume V (cm3) de solution, en supposant une solution diluée et en ignorant la variation de volume du soluté
![]()
En extrayant n1 de l’équation donnant la molalité et en reportant cette valeur dans l’expression de la fraction molaire x2, on obtient :
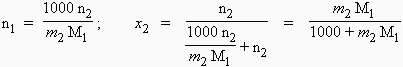
De la même manière, en se rappelant que la densité r est donnée par la relation
![]()
En éliminant le volume V entre cette dernière relation et celle donnant c2, puis en extrayant la valeur de n2 que l’on reporte dans l’expression de x2, on trouve :
| Þ | 
|
Par ailleurs,

La fraction molaire du soluté devient :
![]()
2. Énergie libre et coefficients d’activité d’une solution
L’énergie libre totale d’une solution G est telle que :
| [8.1] |
|
n1 et n2 sont les nombres de moles des composés 1, 2,... et
![]()
les énergies libres partielles molales de chacun de ces composés. De même,
| [8.2] [8.3] |
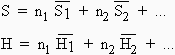
|
Comme G = H - TS, il s’ensuit que
| [8.4] |
|
De même, selon le théorème d’EULER (voir Chapitre III.2),
| [8.5] |
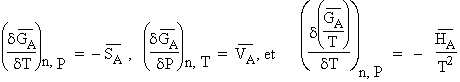 |
et
| [8.6] |
|
en posant aA = xA g'A où
- g'A est le coefficient d’activité et
- xA est la fraction molaire du composé A.
| [8.7] |
|
Nota : Dans le cas d’un composé pur A, xA = 1, Ln aA = 0 car aA = 1 et
![]()
aA = 1 = xAg'A;
aA / xA = g'A = 1 quand xA = 1.
Par conséquent, quand xA = 1, alors g'A = 1 et aA = 1. Dans le cas d’un soluté B, la référence retenue est celle correspondant à une concentration en soluté tendant vers zéro (solution infinie ou très diluée) :
[8.8] aB / xB = g'B = 1 quand xB et aB tendent vers zéro ensemble.
g'B tend vers 1 lorsque xB tend vers 0. Si l’on veut exprimer les concentrations en moles par litre : aB = cB fB ; fB est le coefficient d’activité du soluté pour des concentrations exprimées en moles par litre.
fB = aB / cB = 1
quand cB et aB tendent vers 0 ensemble.
Si l’on veut utiliser la molalité : aB = mB gB ; gB est le coefficient d’activité du soluté pour des concentrations exprimées en molalité.
gB = aB / mB = 1
quand mB et aB tendent vers 0 ensemble. Dans les solutions infiniment diluées,
| [8.9] | gB = fB = g'B. |
3. Formation d’une solution
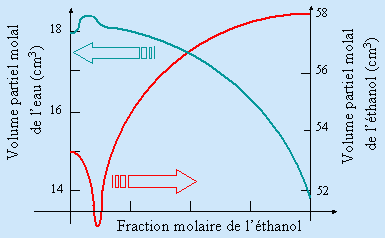
Dans une solution idéale, les propriétés des corps purs sont conservées. Ainsi, si on mélange deux liquides purs miscibles, le volume total de la solution est la somme des volumes des deux liquides mélangés. La formation d’une solution quelconque n’obéit pas nécessairement à cette règle : la solution s’écarte d’autant plus de l’idéalité que le volume résultant s’écarte de la somme des deux liquides constituant le mélange. Ainsi, le mélange eau – éthanol se classe parmi ces derniers. Le volume du mélange d’une mole d’eau (18 cm3 à l’état pur) avec une mole d’éthanol (58 cm3 à l’état pur) produit un mélange dont le volume n’est que de 74,4 cm3, un déficit de près de 1,6 cm3. Dans les cas de grande dilution, l’addition d’une mole d’eau à une très grande quantité d’éthanol n’augmente le volume de la solution que de 14 cm3 et l’addition d’une mole d’éthanol à une très grande quantité d’eau n’ajoute qu’un peu plus de 53 cm3. Cette variation du volume molaire avec l’état de dilution est évidemment une propriété caractéristique de chaque mélange et de chaque composition quantitative (Fig. 8.1).
|
Figure 8.1. Variation du volume molaire (volume partiel molal) de l’eau et de l’éthanol dans leur solution.
La phase eau pure, évidemment constituée de molécules d’eau, contient des régions intermoléculaires vides au sein desquelles les molécules d’éthanol s’insèrent partiellement sous l’effet des forces intermoléculaires (forces de VAN DER WAALS). L’empilement des molécules d'eau est donc perturbé : on obtient un meilleur coefficient de remplissage de l’espace.
En réalisant une solution quelconque, on observe une altération du volume molaire des constituants purs. Il en est de même des grandeurs thermodynamiques. On appelle ces grandeurs modifiées les grandeurs partielles molales. Ainsi le volume partiel molal de l’eau dans une solution éthanolique n’est plus 18 cm3; le volume partiel molal de l’éthanol dans cette solution n’est plus 58 cm3.
Cette grandeur (Y) partielle molale d’un composé i est la contribution d’une mole de ce composé à la propriété globale du mélange. Elle se définit comme étant la dérivée de cette grandeur par rapport au nombre de moles de i à température T, pression P et quantité nj (nombre de moles) de l’autre (des autres) constituants constantes :
![]()
Yi est la pente à la courbe représentant la grandeur totale en fonction de la quantité de i ajoutée, les autres variables T, P et nj demeurant constantes.
On définit ainsi l’enthalpie partielle molale, l’énergie libre partielle molale aussi appelée l’énergie partielle molaire de GIBBS ou mieux le potentiel chimique.
Ces définitions étant faites, regardons ce qui se passe lors de la préparation d«,une solution.
Avant le mélange de nA moles de A avec nB moles de B l’énergie libre totale de ces nA moles de A et nB moles de B est de
| [8.10] | |
Après le mélange, l’énergie libre du mélange, Gm, est :
| [8.11] |
où
![]()
représentent les énergies libres partielles molales des constituants A et B. L’énergie libre de mélange, DGmél, est la différence entre l’énergie libre du mélange et l’énergie libre mesurée avant la réalisation du mélange.
| [8.12] | |
| [8.13] |
où
![]()
sont les variations de l’énergie libre partielle molaire. Cette démonstration est valable pour n’importe laquelle des propriétés dites "extensives", propriétés qui dépendent de la quantité de produits.
| [8.14] [8.15] [8.16] |
 |
[8.17] DGmél = DHmél - T DSmél
En introduisant l'équation [8.6] dans [8.12] :
| [8.18] |
|
[8.19] DGmél = nA RT Ln aA + nB RT Ln aB
En combinant les équations [8.12] et [8.19], on obtient :
| [8.20] |
|
La figure 8.2 montre le comportement comparé des grandeurs DG, DH et TDS d’un système idéal et d’un système réel tétrachlorure de carbone – méthanol.
|
|
Figure 8.2. Diagramme d’un mélange idéal et réel CCl4-CH3OH en trait gras.
Il faut se rappeler que le processus de mélange de deux constituants purs en est un qui augmente le désordre. Par conséquent, sauf exception que l’on verra un peu plus tard, la variation d’entropie au cours du mélange de deux constituants liquides purs est positive, DSmél > 0. Si par ailleurs le processus de mélange est exothermique, l’enthalpie de mélange est négative : DHmél < 0. Il en résulte que la valeur de l’énergie libre de mélange est négative (voir l'équation [8.17]). C’est bien là la caractéristique normale d’un processus spontané (Fig. 8.3A).
Dans les cas où l’enthalpie de mélange est positive (réaction endothermique : DHmél > 0) les situations à envisager sont un peu plus complexes. Disons seulement ici que si la valeur de l’enthalpie de mélange est plus grande que celle du produit T DSmél la valeur de l’énergie de mélange est positive et le processus ne peut se réaliser. On obtient un mélange A + B complètement non miscible (figure 8.3B).
A  B
B
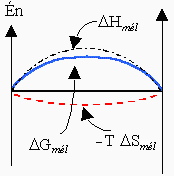
Figure 8.3. Variations des
fonctions thermodynamiques au cours de mélanges : 3A cas des mélanges
exothermiques
et 3B, cas des mélanges endothermiques.
4. Conditions d’équilibre entre phases
Pour qu’il y ait équilibre entre phases d’un même corps pur à température et à pression constantes, il faut que l’énergie libre molaire de la substance soit la même dans chaque phase. Qu’en est-il dans des phases non pures? L’énergie libre totale de chaque phase est donnée par l'équation [8.1]. Supposons que dnA, dnB, etc. moles de A, B, ... sont transférées d’une phase dans une autre. La décroissance de l’énergie libre totale de la phase initiale est :
| [8.21] |
|
L’accroissement de l’énergie libre de la deuxième phase est :
| [8.22] |
|
La variation nette de l’énergie libre totale du système est :
| [8.23] |
|
car dnA = - dnA'. À l’équilibre, DG = 0. Puisque l’échange de A se fait indépendamment de celui de B, dnA et dnB sont des variables indépendantes, il faut donc que
| [8.24] |
| À l’équilibre, l’énergie libre partielle molale de chaque constituant est la même dans chaque phase. |
5. Solutions idéales
Par définition, une solution est dite idéale lorsque l’activité de chacun de ses constituants est égale aux fractions molaires sous conditions de température et de pression ou encore lorsque les coefficients d’activité sont égaux à l’unité quelles que soient les conditions de pression, de température et de composition.
aA = xA g'A avec g'A = 1 (idéalité)
[8.25] DGmél = nA RT Ln xA + nB RT Ln xB
Le membre de droite de la précédente égalité étant indépendant de la pression,
| Þ |
|
Le mélange de deux constituants formant une solution idéale se fait sans changement de volume. De plus, et pour la même raison, puisque
| [8.26]
Þ |
|
Le mélange de constituants d’une solution idéale se fait sans variation d’enthalpie et donc sans dégagement ou absorption de chaleur : DGmél = - T DSmél .
[8.27] Þ DSmél = -[nA R Ln xA + nB R Ln xB]
Pour une solution idéale, la variation d’entropie au cours de la formation de la solution à partir de ses constituants purs ne dépend que de la quantité et des concentrations des constituants.
|
|
Figure 8.4. Variation de l’enthalpie, de l’énergie libre de mélange et
de l’entropie
au cours d’un mélange idéal de deux composés purs A et B.
6. Équilibre entre une solution et sa phase vapeur
En phase vapeur, gazeuse, d'après l'équation [8.7]
| [8.28] |
|
GA(g) représente l’énergie libre du composé A dans la phase vapeur. En solution, on a l'équation [8.8]
| [8.29] |
|
À l’équilibre, l'énergie libre du constituant A est la même dans chacune des deux phases :
[8.30] GA(g) = GA(sol)
| [8.31]
|
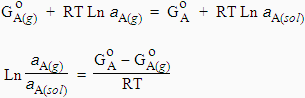 |
Si la température est fixée, donc connue,
![]()
Donc, le rapport aA(g) / aA(sol) est une constante : aA(g) / aA(sol) = K. Pour A pur, aA(sol) = 1, on obtient
![]()
La grandeur |
|
est la fugacité de la vapeur au-dessus du liquide pur. |
Donc, K = |
et
| [8.33] |
|
Loi de RAOULT généralisée. |
|
À nouveau si

Si la vapeur est idéale :
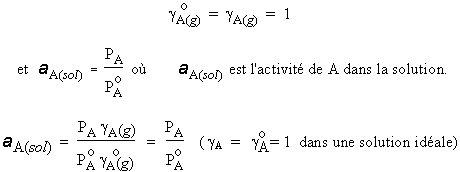
Cette activité est donc obtenue par des mesures de pression. Pour une vapeur idéale, la relation [8.19] entraîne :
| [8.34]
|
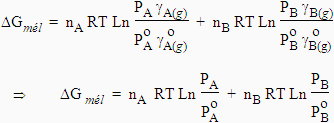 |
7. Pressions de vapeur d’une solution idéale
Soit un mélange A et B miscibles en toutes proportions à l’état liquide et supposons que le mélange gazeux soit idéal. Si de plus xA et xB sont les fractions molaires des composés A et B en phase liquide, les activités de ces composés en phase liquide sont :
aA = xA et aB = xB
| [8.35] |
C’est l’expression de la loi de RAOULT.
La pression partielle d’un constituant volatil idéal au-dessus d’une solution est égale à la pression de vapeur saturante de ce composé pur multiplié par sa fraction molaire dans la solution. |
| [8.36]
[8.37] |
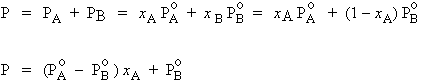
|
Pour n’importe quel système binaire, les pressions
![]()
sont déterminées par la température et la pression P est donc une fonction linéaire des fractions molaires xA et xB (Fig. 8.5).
|
|
Figure 8.5.
Comportement des pressions dans un système binaire idéal
en situation isotherme.
8. Pressions partielles réelles de vapeur d’un mélange binaire
8.a Mélange à déviation positive
Pour un mélange donné, la pression totale est supérieure à la somme des produits des pressions de vapeur saturante de chacun des constituants par leur fraction molaire. La solution cyclo-C6H12-CCl4 (Fig. 8.5a) en est un exemple :
|
|
Figure 8.5a. Diagramme
isotherme à déviation positive.
8.b Mélange à déviation négative
Pour un mélange donné, la pression totale est inférieure à la somme des produits des pressions de vapeur saturante de chacun des constituants par leur fraction molaire. Exemple (Fig. 8.5b) :
|
|
Figure 8.5b. Diagramme isotherme à déviation négative.
Dans les deux précédents cas, il faut interpréter la faible déviance, ou mieux la quasi idéalité de ces systèmes binaires, par le fait qu’il n’y a pas ou qu’il y a très peu d’interactions entre les molécules en phase liquide que ce soit entre les molécules de même identité ou entre celles de nature différente.
8.c Déviation positive avec maximum (azéotropisme positif)
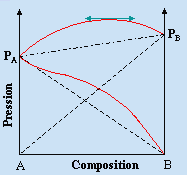
C'est l'équivalent du mélange à déviation positive avec la caractéristique supplémentaire suivante : la pression totale en équilibre au-dessus du mélange passe par un maximum. Exemple : eau-C2H5OH; méthylal-CS2 (Fig. 8.6);...
 |
 |
Figure 8.6. Diagrammes isotherme et isobare de système azéotropique positif.
Il faut noter qu'à la tension de vapeur la plus basse correspond la température d'ébullition la plus haute. Sur la figure 8.6, pour une température donnée, le composé A a une pression de vapeur plus basse que celle du composé B. À une pression déterminée, il a de ce fait une température d'ébullition plus élevée que celle de B.
Une déviation positive importante produisant éventuellement un azéotropisme avec maximum trouve son origine dans le fait que les interactions en phase liquide entre les molécules A et les molécules B sont plus faibles que les interactions entre les molécules de même espèce. L’ajout des molécules B vient perturber les interactions de type A-A et les interactions A-B sont plus faibles augmentant ainsi la volatilité du composé A. On interprétera les cas extrêmes comme résultant d’une répulsion mutuelle des deux constituants du mélange (cas du mélange toluène - éthanol). Le système sera aussi appelé azéotrope à point d’ébullition minimum.
8.d Déviation négative avec minimum (azéotropisme négatif)
C'est l'équivalent du mélange à déviation négative avec la caractéristique supplémentaire suivante : la pression totale en équilibre au-dessus du mélange passe par un minimum. La diminution de la pression se traduit par une augmentation de la température de distillation. La distillation est aussi appelée à température maximum. Dans le présent cas les forces intermoléculaires entre les molécules A et B sont plus fortes qu’entre les molécules de même identité. Il y a donc une diminution de la volatilité des deux constituants.
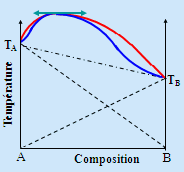
exemple : eau - HNO3; acétone - chloroforme (Fig. 8.7); ...

|
|
Figure 8.7. Diagrammes isotherme et isobare de système azéotropique négatif.
Tableau 8.1. Température d’ébullition et composition de quelques azéotropes
Type |
A |
B |
Téb (ºC) |
% de A |
maximum |
eau |
éthanol |
78,15 |
4,43 |
eau |
propanol |
88,1 |
28,2 |
|
éthanol |
benzène |
67,8 |
32,4 |
|
minimum |
eau |
acide nitrique |
121,0 |
31,5 |
acétone |
chloroforme |
64,7 |
20,0 |
9. Solubilité de liquides partiellement miscibles
On a vu que la condition de mise en solution correspond à une valeur négative de l’énergie libre de mélange. Plus précisément, lorsque la réaction de mélange est exothermique, DHmél < 0, l’énergie libre de mélange est négative et le système de deux constituants purs A et B est totalement miscible. On observe la formation d’une solution sur toute l’échelle de concentrations. Si au contraire le mélange est un processus endothermique, DHmél > 0, et si de plus la valeur de l’enthalpie de mélange est supérieure au produit de la température par l’entropie de mélange, DHmél > T DSmél , le mélange est au contraire non miscible.
Dans les cas où l’inégalité précédente se transforme en une quasi-égalité, DHmél » T DSmél, la situation est plus complexe. On le voit (Fig. 8.8) la quasi égalité dépend de la valeur de la température. Il existe une température critique, TC, au-dessus de laquelle DHmél < T DSmél, l’énergie libre de mélange est négative. Réciproquement, en dessous de cette température critique, l’inégalité est inversée et l’énergie libre de mélange est positive. Le mélange A + B n’est plus miscible. En fait le mélange A + B passe d’une situation de miscibilité totale à une situation de non miscibilité complète lorsque la température passe de TC + DT à TC – DT. Les valeurs respectives de DHmél et de T DSmél étant voisines, l’effet de concentration joue. On obtient plutôt la situation décrite à la figure suivante.
|
|
Figure 8.8. Énergie libre de mélange dans un système partiellement miscible.
À faible concentration de B dans A, le terme T DSmél est plus important que le terme DHmél : DGmél est négatif et le mélange A + B est miscible. En ajoutant davantage de B, l’énergie libre de mélange continue à décroître et atteint pour une concentration x'B une valeur minimum : un ajout supplémentaire de B ferait croître cette énergie de mélange, ce qui est inacceptable. Au-dessus de cette valeur x'B le mélange devient non miscible. La situation est en général similaire du coté de B pur de telle sorte qu’il existe une plage de non miscibilité entre x'B et x"B. Ce cas correspond au diagramme eau – aniline décrit plus bas.
On a déjà indiqué plus haut qu’en général l’entropie de mélange est positive. Il existe des situations dans lesquelles l’entropie de mélange est négative, DSmél < 0. Lorsque l’addition de B dans A se traduit par une augmentation de l’ordre, comme par exemple dans le cas de formation de liaisons hydrogène, le système acquiert un plus haut degré d’ordre : DSmél < 0. Dans ces cas, l’enthalpie de mélange est fortement négative de telle sorte que l’énergie libre de mélange est encore négative. L’ordre créé par l’apparition de liaisons hydrogène est de plus en plus perturbé par l’augmentation de température. L’entropie de mélange diminue avec l’augmentation de la température T. Cette situation correspond à une température critique minimum telle qu’apparaissant dans le cas du mélange eau – triéthylamine décrit plus bas. Il existe des cas où l’augmentation de température se traduit par une inversion du signe de l’énergie libre de mélange. Le cas du mélange eau – nicotine cumule les deux températures critiques : celle à maximum et celle à minimum. D’autres enfin où expérimentalement on ne peut observer ces extremums (Fig. 8.9).
1- 1e type : courbe de solubilité à température maximum
exemple eau-aniline.
2- 2e type : courbe de solubilité à température minimum
exemple eau-triéthylamine.
3- 3e type : courbe de solubilité à température maximum et minimum
exemple eau-nicotine.
4- 4e type : courbe de solubilité à température sans extremum
exemple eau-éther diéthylique.
 |
 |
 |
 |
| Tmax = 168 ºC | Tmin = 18,5 ºC | Tmax = 205 ºC et Tmin = 60,8 ºC |
pas d’extremum observable |
| 1e type | 2e type | 3e type* | 4e type |
Figure 8.9. Exemples de binodales de non miscibilité en phase liquide.
*(Ces résultats ont été obtenus alors que les échantillons sont en équilibre avec leur vapeur dans des tubes scellés).
Détermination des extremums des binodales
À une température donnée T, dans un système donné, on observe la séparation d’un mélange de deux constituants liquides en deux phases appelées phases conjuguées. Les compositions de ces deux phases conjuguées est donnée par la projection des points A et B sur l’axe horizontal (Fig. 8.10). Au fur et à mesure que la température augmente (ou diminue), le segment AB devient A'B', puis A"B", ... La détermination des extremums de binodale n’est pas toujours évident. Une méthode consiste à tracer le lieu géométrique des milieux des segments conjugués AB, A'B', A"B"... Ce lieu géométrique est appelé le diamètre rectilinéaire (Fig. 8.10). L’intersection de ce lieu géométrique avec la binodale précise le sommet S.
|
|
Figure 8.10. Détermination du diamètre rectilinéaire.
10. La règle des moments chimiques
|
|
Figure 8.11. Théorème des moments chimiques.
Soit x la composition globale de B d’un mélange de deux corps purs A et B (Fig. 8.11). Soient xA et xB les concentrations de B respectivement dans chacune des phases a et b (a est riche en A et b est riche en B). Soient w la masse totale du mélange et wA et wB les masses respectives des phases a et b.
w = wA + wB et x w = xA wA + xB wB
En divisant ces deux équations membre à membre, on obtient :
![]()
Þ
xA wA + xB wB = x ( wA + wB ) wA (xA - x) = wB (x - xB)
| [8.38] |
Le rapport des masses des phases riches en A et B, a et b, est égal au rapport des segments opposés. |
11. Pression de vapeur et diagramme de distillation d’un mélange de deux liquides partiellement miscibles
Soient deux liquides partiellement miscibles A et B. Les courbes d’ébullition et de rosée sont en quelque sorte télescopées par la binodale délimitant la zone de non miscibilité en phase liquide. On obtient le diagramme montré en figure 8.12. Le segment de contact mettant en équilibre les deux liquides L1 et L2 et la phase vapeur correspond à une température invariante. En effet, l’application de la règle des phases (voir équation [7.1], Chapitre VII.2.b) indique que le système est invariant en présence de trois phases (la pression est fixée) :
u = C + 2 - j = 2 + 1 - 3 = 0
Figure 8.12. Diagramme isobare eau - isobutanol.
La distillation d’un tel mélange est similaire à celle d’un azéotrope présentant un tel minimum. Dépendant de la composition du mélange, on obtiendra en haut de la colonne de rectification le mélange à 66 % d’isobutanol et en bas, dans la cuve, l’eau ou l’isobutanol pur. Il existe des cas limites où les deux liquides purs sont complètement immiscibles : Fig. 8.13. On a déjà indiqué que l’énergie libre de mélange est positive sur toute l’échelle de concentration entre A pur et B pur.
|
|
Figures 8.13. Diagrammes de systèmes binaires totalement non
miscibles
(Note : les échelles de température sont quelconques).
12. Équilibres chimiques en solution
Soit la réaction :
![]()
| En général : |  |
[8.39] Ka = Kc Kg et Ka = Kc en solution idéale.
13. Cas des solides peu solubles : le produit de solubilité Ksol ou KPS
Un cas intéressant et important d’une solution hétérogène est celui de la solubilité de solides ioniques peu solubles dans l’eau. Après avoir immergé un sel peu soluble, par exemple le perchlorate de potassium KClO4 et avoir agité suffisamment la solution, une faible partie seulement de ce perchlorate est passé en solution. La solution est alors saturée en perchlorate de potassium. L’équilibre atteint implique les ions potassium K+ et perchlorate ClO4- et le perchlorate solide.
KClO4 (solide)
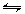 K+(aqueux) + ClO4-(aqueux)
K+(aqueux) + ClO4-(aqueux)
Pour
cette réaction, la constante d’équilibre Ksol
est telle que :
Ksol = [K+]
[ClO4-]
Ksol est encore appelé le produit de solubilité. Dans n’importe quelle solution saturée en perchlorate de potassium, le produit des activités des ions potassium [K+ et perchlorate [ClO4-] est égal à Ksol. Cette relation est aussi valable pour n’importe quel sel peu soluble comme par exemple le CuCl … Si le sel se dissocie en plusieurs ions, le produit de solubilité doit être corrigé en conséquence. Ainsi pour un sel de type AmBn en équilibre avec les ions A+ et Cl- on obtient :
8.40
Ksol
= [A+]m
[B-]n
Ksol = [Ba++]1
[Cl-]2
Dans
cette expression, les concentrations sont exprimées en nombre de moles
d’ions/litre de solution. Le
tableau 8.2 donne quelques valeurs du produit de solubilité.
Tableau 8.2. Produit de solubilité de quelques solides ionisés dans l’eau à 25 °C
| Composé | Ksol | Composé | Ksol | Composé | Ksol |
| AlPO4 | 9,83 10-21 | PbCl2 | 1,17 10-5 | Ca(OH)2 | 5,27 10-15 |
| BaCO3 | 2,58 10-9 | Pb(SCN)2 | 2,11 10-5 | Fe(OH)2 | 4,87 10-17 |
| CuCl | 1,72 10-7 | Hg2SO4 | 7,99 10-7 | Fe(OH)3 | 2,64 10-39 |
| MnS | 4,65 10-14 | Ag2C2O4 | 1,12 10-12 | Mn(OH)2 | 2,06 10-13 |
| ZnS | 2,93 10-25 | Sr3(AsO4)2 | 4,29 10-19 | Sn(OH)2 | 5,45 10-27 |
|
Tiré
du Handbook of Chemistry and Physics, 70e édition, CRC
Press, 1989-1990, B-207 – B-208. |
|||||
Ce
tableau indique si besoin était que cette notion de produit de solubilité
n’est pas restreinte aux sels. La
notion de produits de solubilité est aussi applicable aux hydroxydes.
On peut aussi l’étendre à d’autres sels peu solubles dans
d’autres solvants …
Un
effet intéressant est celui appelé effet de sels.
En effet que se passe-t-il lorsqu’on ajoute deux sels peu solubles dans
l’eau, deux sels qui par ailleurs ont un ion commun ?
Par exemple, si l’on ajoute du sulfure de manganèse MnS à une
solution déjà saturée en sulfure de zinc, les produits de solubilité de
chacun des deux sels continuent de s’appliquer.
La concentration d’ions sulfures [S2-]
est maintenant plus élevée que celle d’ions manganèse [Zn++]
puisque la relation entre les concentrations des ions est donnée par :
[S2-]
= [Mn++]
+ [Zn++]
La concentration des ions Zn++ diminue donc au fur et à mesure qu’on ajoute du sulfure de manganèse. Le même phénomène a lieu si au lieu du sulfure de manganèse on ajoute du sulfure de sodium, un sel très soluble.
En fait, la relation [8.40] n’est pas tout à fait exacte. En lieu et place des concentrations il serait plus approprié d’introduire les activités des ions de telle sorte que cette relation [8.40] s’écrit plutôt :
| 8.41 |
|
14. Conclusions L’application des lois de la thermodynamique montre qu’une solution idéale se fait sans variation de volume et sans dégagement de chaleur. La variation d’entropie entraîne une variation de l’énergie libre. Ce n’est évidemment pas le cas d’une solution réelle dans laquelle les interactions entre les molécules de solvant et les molécules de soluté sont importantes. Dans le cas de solution très diluées, l’application des mêmes lois permettent de retrouver la loi de RAOULT. Finalement, dépendant de l’importance relative des interactions entre les molécules de A d’une part, de B d’autre part et entre les molécules A et B, on obtient des mélanges à déviation positive ou négative, avec dans les cas les plus loin de l’idéalité des mélanges azéotropiques. La distillation d’un mélange de deux liquides peu ou pas miscibles est similaire à celle d’un azéotrope présentant un minimum.
|
15.1. Calculez la molarité et la fraction molaire d’une solution qui contient 10,0 g de HCl dans 100,0 ml de solution : 1 mole de HCl = 36,5 g.
Réponse : xHCl = 4,7 %.
15.2. À 35 ºC la tension de vapeur de CS2 pur est de 512 mmHg et les tensions de vapeur de ce composé dans l’acétone sont :
N CS2 |
0,005 |
0,01 |
0,015 |
0,18 |
0,5 |
PCS 2 (mmHg) |
10 |
19,8 |
29,2 |
258 |
404 |
a. Calculez le coefficient d'activité du CS2 dans l'acétone dans chacun des cas. Quel est le coefficient de la loi de HENRY ?
b. Si on prend le CS2 pur comme état de référence :
1- donner le coefficient d'activité de CS2 pur et
2- donner le coefficient d'activité de CS2 dans les solutions 0,18 et 0,5.
c. Si on prend la solution infiniment diluée comme état de référence, quelle est l’activité du CS2 dans les solutions 0,18 et 0,5 et pour CS2 pur ?
Réponse : g = 2000 pour NCS2 = 0,005.
15.3. Un mélange de toluène et de benzène contient 30 % en poids de toluène (C6H5-CH3). À 30 ºC, la pression de vapeur saturante du toluène est de 36,7 mmHg et celle du benzène est de 118,2 mmHg. En supposant que ces deux composés aromatiques forment une solution idéale, calculez la pression totale ainsi que les pressions partielles de chaque composé au-dessus de la solution à 30 ºC.
Réponse : P(totale) = 96,48 mmHg.
15.4. À la température de 60 ºC la pression de vapeur saturante de l’éthanol est de 327,7 mmHg et celle du méthanol est de 625 mmHg. Un mélange de ces deux alcools, mélange que l’on considérera idéal, contient 50% en poids de chacun des deux composés. Quelle sera la composition de la vapeur en équilibre à 60 ºC ?
Réponse : yCH3OH = 0,733.
15.5. Une solution de deux liquides volatiles, A et B, suit la loi de RAOULT. À une certaine température, la pression en équilibre au-dessus de la solution est de 400 mmHg, la fraction molaire de A est de 0,45 dans la phase vapeur et de 0,65 dans la phase liquide. Quelles sont les pressions de vapeur saturante de chacun de ces deux liquides ?
Réponses : P°B = 629 mmHg et P°A = 277 mmHg.
15.6. À 60 ºC, le système eau–phénol se partage en deux phases liquides : la première contient 16,8 % de sa masse en phénol et la seconde 44,9 % de sa masse en eau. Quelle est la masse de chacune des deux phases sachant que ce système contient 90 g d’eau et 60 g de phénol ?
Réponses : 59,1 g de phase aqueuse et 90,9 g de solution phénolique.
15.7. À 300 K un liquide A a une pression de vapeur de 280,0 mmHg et celle d’un liquide B est de 170 mmHg. On prépare une solution équimoléculaire de ces deux liquides et la pression de vapeur de ce mélange est de 380 mmHg. On observe également que la fraction molaire de A dans cette phase vapeur est de 0,60. En supposant que ce mélange se comporte comme un système idéal, calculez :
Réponses : DGmél = - 798 joules et DGmél = - 3 456 joules pour le mélange idéal.
15.8. La tension de vapeur du monométhyl éther de l’éthylène glycol (A) et du monoéthyl éther de l’éthylène glycol (B) sont respectivement de 154,4 et de 102,2 mmHg à 80 ºC. À partir de ces résultats, calculez la composition de la phase gazeuse en fonction de celle de la phase liquide en équilibre pour tout le domaine des de concentration du mélange binaire des deux éthers, en supposant que le mélange obéit à la loi de RAOULT et représentez-la graphiquement sur le diagramme yA = ¦ (xA) à 80 ºC. On calculera les valeurs demandées pour les concentrations xA = 0,0; 0,1; 0,2; 0,3;… 0,9 et 1,0.
15.9. Activité du carbone dans l’acier
1. Dans un tube en quartz, on introduit de l’oxyde de strontium, SrO, du carbonate du même métal, SrCO3 et du carbone graphite C. On élimine l’air dans la cellule que l’on scelle. On la porte à la température de 1120 K. On observe une pression totale dans la cellule de 172,5 mmHg. S’il n’y avait pas eu de carbone, suite à la décomposition du carbonate, la pression aurait été de 2,5 mmHg. Calculer le KP de la réaction (a) à 1120 K. Quel est l’avantage d’ajouter du carbone?
[a] CO2 (g) + C (graphite) ![]() 2 CO (g)
2 CO (g)
2. À 300 K, l’enthalpie de formation du gaz carbonique est de - 393 kJ/mol et l’enthalpie de combustion d'une mole d’oxyde de carbone est de - 283 kJ. En déduire celle de la réaction (a) à la même température (en l’absence des Cp, on négligera les variations des enthalpies de formation avec la température).
3. Démontrer que si la pression P et la température T sont fixées, le rapport x2CO/xCO2, où x désigne les fractions molaires, est constant (égal à z) et exprimer la fonction log z en fonction de la température T et de la pression P.
4. En appelant x le titre (pourcentage) en oxyde de carbone du mélange gazeux à l’équilibre, donner graphiquement la relation entre P et x à température constante (P en ordonnée) et discuter brièvement de l’allure des courbes.
5a. L’équilibre (a) a été étudié à 1270 °C mais en remplaçant le carbone par des feuilles d’acier à austénite (solution de carbone dans du fer) que l’on maintient en équilibre des mélanges CO et CO2. En fixant le rapport P2(CO)/P(CO2) à une valeur définie z, on obtient les fractions molaires NC du carbone dans l’acier. En fonction de z, on trouve les valeurs données dans le tableau suivant (KP = 135 atm) :
| z | 2,00 | 3,06 | 6,06 | 13,2 | 41,6 | 86,4 |
| NC | 0,002 | 0,003 | 0,006 | 0,012 | 0,032 | 0,054 |
Montrer comment pour chaque valeur de NC on peut calculer l’activité a'C et le coefficient g'C du carbone en solution dans le fer. On effectuera les calculs pour NC = 0,006.
5b. En prenant comme référence la solution diluée, montrer
que dans l’intervalle
0,00 < xC < 0,054 où la solution obéit aux lois des solutions diluées, on
doit avoir z/xC = constante et indiquer à quelle valeur de
NC on s’éloigne d’un tel comportement.
5c. Par quel coefficient faudrait-il multiplier les valeurs de g'C pour obtenir les coefficients gC lorsqu’on choisit comme état de référence la solution infiniment diluée ?
6. Le mélange obtenu en 1-, à 1120 K, est rapidement refroidit à 600 ºC sous une pression de 0,25 atm. Dans ces conditions le titre en oxyde de carbone doit être de 0,40. Le mélange obtenu à 1120 K est-il stable? Comment évolue-t-il? Pour étayer votre affirmation, calculer la variation du nombre de moles de CO et de CO2 à partir d’un mélange initial total à 1120 K de 1 mole (CO + CO2).
7. Au-dessus de 570 ºC, on a les réactions suivantes :
[b] CO (g) + Fe3O4 ![]() CO2 (g) + 3 FeO
CO2 (g) + 3 FeO
[c] CO + FeO ![]() CO2 + Fe
CO2 + Fe
Le pourcentage de CO en phase gazeuse, x, varie selon les lois suivantes :
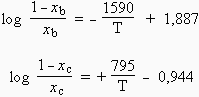
a) Sachant que les enthalpies ne varient pas avec la température, justifier ces expressions.
| b) À quelle température les droites |
|
se coupent-elles? |
Comment se présentera l’équilibre au-dessus de cette température?
Dernière mise à jour : 2021-07-09
x x x x x x x x x x x x