1. Introduction
Google Trends est un outil offert gratuitement par la multinationale Google permettant d’évaluer la popularité d’un ou plusieurs termes de recherche utilisé(s) par les internautes dans le moteur de recherche éponyme.
Les données proposées par cet outil peuvent être téléchargées sous l’interface du logiciel R à l’aide de la bibliothèque gtrendsR. La base de données produite contient notamment le nombre de hits mensuels portant sur le ou les termes recherchés. L’indice de popularité appelé hits n’indique pas un nombre de recherches absolu, mais une proportion entre 0 et 100, où 100 représente la quantité maximale d’utilisation du terme dans le mois et la zone géographique éventuellement circonscrite.
Google Trends n’a pas pour vocation à fournir le volume d’une recherche, mais permet seulement de visualiser l’évolution de sa popularité.
Les données de Google Trends sont disponibles mensuellement depuis 2004.
Dans le cadre de cette exploration, nous nous intéresserons à l’évolution de la popularité de l’acronyme de l’Université du Québec à Chicoutimi UQAC dans les requêtes des internautes.
La fonctionnalité de cet outil qui vise à déterminer la position géographique de l’internaute effectuant la requête a été améliorée à partir du 1erjanvier 2011. La collecte des données a, pour sa part, été améliorée à partir du 1er janvier 2016. Les résultats suivants sont donc à interpréter avec prudence.
2. Description générale des tendances
tendances <- gtrends(keyword = c("UQAC"),
time = "2004-01-02 2019-09-30",
gprop = "web",
low_search_volume=TRUE)
Les données utilisées pour déterminer la popularité relative du terme UQAC dans les requêtes des internautes s’échelonnent du 1er février 2004 au 30 septembre 2019. Aucune restriction géographique n’a été effectuée. Les données récoltées ne sont donc pas circonscrites à un pays ou une région donnée. Cette collecte comprend aussi les résultats pour les zones géographiques de faible volume.
Comme indiqué par Simon Rogers (Data journalist et Data Editor chez Google) en 2016 :
« There are two ways to filter the Trends data: real time and non-real time. Real time is a random sample of searches from the last seven days, while non-real time is another random sample of the full Google dataset that can go back anywhere from 2004 to ~36 hours ago. The charts will show you either one or the other, but not both together, because these are two separate random samples. We take a sample of the trillions of Google searches, because it would otherwise be too large to process quickly. By sampling our data, we can look at a dataset representative of all Google searches, while finding insights that can be processed within minutes of an event happening in the real world. »
Les données récoltées sont extraites d’un échantillon aléatoire archivé des trillions de requêtes soumises par les internautes à ce moteur de recherche.
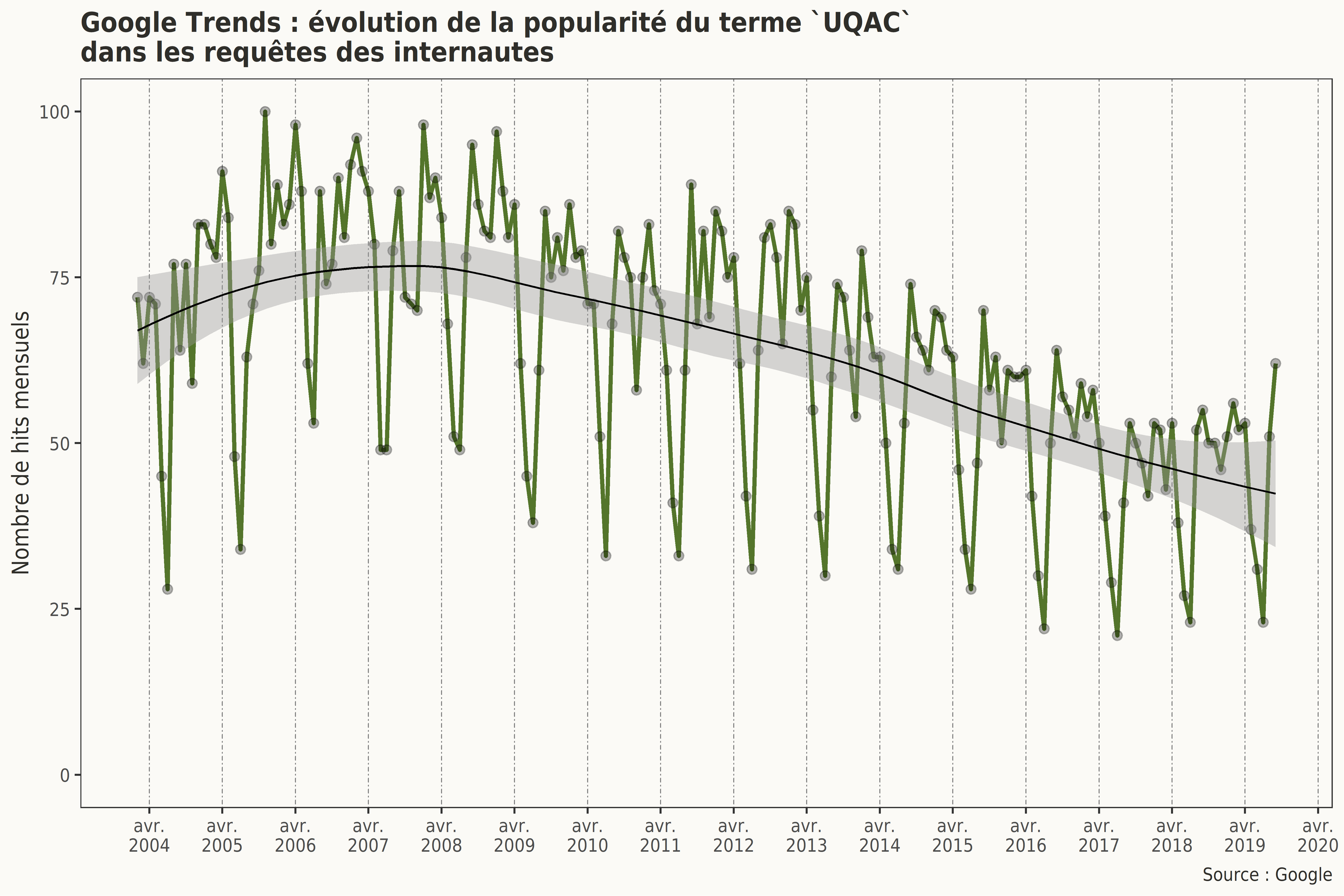
À priori, il semble que le nombre de hits du terme UQAC diminue au cours du temps, passant, en moyenne, de 74 de 2004 à 2007, à 45 entre 2017 et 2018. Le nombre de hits du terme UQAC semble à nouveau à la hausse en 2019.
À ces résultats mensuels, a été ajoutée une courbe de lissage par régression locale (Locally Weighted Scatterplot Smoother). Ce type de régression dite loess (ou lowess) repose sur la technique des k plus proches voisins (KNN). Cette courbe tend à confirmer cette tendance générale.
Cette représentation exploratoire met également en lumière une possible composante saisonnière dans cette série temporelle.
D’année en année, les mois de juin, juillet et décembre, qui correspondent aux périodes de vacances, semblent présenter un nombre inférieur de requêtes. À l’inverse, les mois d’août/septembre et de janvier, qui correspondent, eux, aux périodes de rentrée, semblent présenter une hausse récurrente du nombre de hits du terme UQAC.
En bref, en explorant ces données on note une double tendance non linéaire du nombre du hits : une tendance générale à la décroissance, une saisonnalité annuelle.
3. Une modélisation de cette série temporelle
La modélisation d’une série temporelle vise à choisir un modèle qui décrit au mieux les données collectées. Une modélisation doit être à même d’extraire une structure du signal :
- en supprimant le bruit, les erreurs de mesure ou les fluctuations aléatoires non explicables ;
- en recherchant la présence d’une tendance et éventuellement d’une saisonnalité dans les données.
3.1 Les modèles additifs généralisés (GAM)
Afin de confirmer statistiquement les informations exploratoires, nous avons choisi d’utiliser un modèle additif généralisé.
Les modèles additifs généralisés (Generalized additive models) s’avèrent pertinents lorsque la relation entre un prédicteur continu (ici le temps) et une variable dépendante (ici le nombre de hits) n’est pas décrite adéquatement par une régression linéaire (Wood, 2017).
Une régression linéaire ne permet pas de saisir la nature non linéaire d’une trajectoire temporelle par exemple. De telles divergences entre les données et le modèle créent des patrons dans la représentation des résidus (un résidu est la différence entre la valeur prédite par un modèle et la valeur réelle de la variable dépendante), ce qui rend les intervalles de confiance et les valeurs p non fiables (Sóskuthy, 2017). L’utilisation d’une régression linéaire pour décrire une relation non linéaire entre un prédicteur et une variable dépendante est donc un choix dangereux. Les GAM permettent de faire fi de cette difficulté en utilisant des fonctions de lissage (smoothers) non paramétriques appliquées à un ou plusieurs prédicteurs qui peuvent, bien entendu, être accompagnés de covariables paramétriques classiques.
La fonction de lissage par défaut d’un GAM est un thin plate spline (Spline en plaque mince), mais de nombreuses autres fonctions de lissage adaptées à différentes situations (notamment la cyclicité d’un phénomène) sont aussi disponibles (cubic regression spline, cyclic spline, penalised spline…)
“While the differences between all these smoothers are beyond the scope of this article, it matters to say that the so-called penalization aims at finding the best value for the smoothing parameter, which controls the amount of smoothing, i.e., the degree of fitting of the smooth term to the raw predictor(s), unless this degree is specified externally by the user. The effective degrees of freedom (edf) can be referred to describe the amount of smoothing. The goal is here to avoid both underfitting and overfitting – the bias/variance tradeoff, so that the model can generalize well to data other than the sample used to build it.” — Coupé (2018 : 8)
3.2 Un modèle parcimonieux
3.2.1 La parcimonie d’un modèle
Une propriété de base d’un modèle statistique de qualité est qu’il est à même d’expliquer convenablement les données tout en éliminant les détails et les erreurs. De tels modèles sont appelés « parcimonieux ». En recourant à la métrique de l’AIC (Akaike’s Information Criterion), nous avons cherché à mettre au jour le modèle parcimonieux et donc à sélectionner :
- les variables indépendantes importantes ;
- les smoothers les plus appropriés.
“The AIC: value is a corrected version of the deviance that has the additional benefit that it can be compared across models (for the same data set and response variable) with different numbers of predictors.” — Speelman (2014: 510)
Il n’existe pas de théorie statistique permettant d’établir un seuil de signification strict (une valeur p) pour l’utilisation de l’AIC. La sélection du modèle parcimonieux se fait alors en identifiant le modèle ayant la plus petite valeur d’AIC. Généralement, si les modèles se trouvent à moins de 2 unités AIC l’un de l’autre, ils sont très similaires. S’ils ont plus de 10 unités de différence entre les deux modèles, ils sont très différents et il est important de considérer le modèle ayant la plus petite valeur d’AIC.
Dans le cadre de cette première exploration,, trois fonctions de lissage sont testées : thin plate spline (tp) (par défaut), cubic regression spline (cr) et cyclic cubic regression spline (cc) (bien adaptée aux évènements cycliques comme les variations mensuelles).
Le nombre de noeuds (knots) est en lien avec les lieux de changement de direction de la courbe de lissage. Le nombre de noeuds dépend de la taille de l’échantillon et du nombre d’observations par variable lissée. Plus il y a de noeuds et plus la fonction de lissage va se montrer sautillante (wiggly) et tenter de suivre parfaitement l’évolution temporelle des données au risque d’être sur-ajustée. Déterminer le nombre optimal de noeuds est donc important pour mettre au point un modèle parcimonieux.
Pour la variable mois, le nombre maximal de noeuds est fixé à 12 (le nombre de mois dans une année) et pour la variable annee, il est fixé à 16 (soit le nombre d’années couvertes dans cet échantillon).
3.2.2 Modèles évalués
Différents modèles sont comparés ci-dessous afin d’établir un modèle parcimonieux.
modele1 <- gam(hits ~
s(mois, k=12, bs="tp")
+ s(annee, k=16, bs="tp"),
method = "GCV.Cp",
data=tendances.df,
family = "poisson",
select=T
)
modele2 <- gam(hits ~
s(mois, k=12, bs="cc")
+ s(annee, k=16, bs="tp"),
method = "GCV.Cp",
data=tendances.df,
family = "poisson",
select=T
)
modele3 <- gam(hits ~
s(mois, k=12, bs="cc")
+ s(annee, k=16, bs="cr"),
method = "GCV.Cp",
data=tendances.df,
family = "poisson",
select=T
)
3.2.3 Comparaison par AIC
La comparaison de ces modèles en fonction de leur valeur d’AIC suggère que le modèle1 est le plus parcimonieux. Il va de soi que la différence entre le modele2 et le modele3 est minime.
df AIC
modele1 17.08252 1259.162
modele2 16.79017 1276.164
modele3 16.77871 1276.146
3.2.4 Résumé du modèle choisi
Family: poisson
Link function: log
Formula:
hits ~ s(mois, k = 12, bs = "tp") + s(annee, k = 16, bs = "tp")
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.113751 0.009563 430.2 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(mois) 10.307 11 496.2 <2e-16 ***
s(annee) 5.775 15 374.7 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.881 Deviance explained = 90.2%
UBRE = -0.25036 Scale est. = 1 n = 188
La fonction de lien indiquée dans le résumé du modèle associe les prédictions d’un modèle sur l’échelle de réponse à celles sur l’échelle du prédicteur linéaire. Les données de comptage (ici les hits) sont des valeurs entières strictement non négatives et sont modélisées par un GAM utilisant une distribution de Poisson et une fonction de lien log. Sur l’échelle logarithmique, la réponse peut prendre n’importe quelle valeur réelle entre –∞ et +∞, et c’est sur cette échelle que l’ajustement du modèle est effectué. Cependant, nous devons faire correspondre ces valeurs à l’échelle de réponse, qui, elle, est non négative. L’inverse de la fonction de lien, soit ici la fonction exponentielle est alors utilisée pour rééchelonner les valeurs prédites par le modèle sur l’intervalle 0 +∞.
D’après les informations fournies dans ce résumé, les effets des deux effets fixes continus lissés mois et annee sont significatifs. Puisque les niveaux de significativité statistique proposés dans ce résumé sont des approximations, il est important que le modèle soit vérifié.
3.3 Quelques diagnostics de base
Method: UBRE Optimizer: outer newton
full convergence after 18 iterations.
Gradient range [-4.546141e-10,4.212817e-09]
(score -0.2503571 & scale 1).
eigenvalue range [-4.212816e-09,0.005652646].
Model rank = 27 / 27
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(mois) 11.00 10.31 1.15 0.98
s(annee) 15.00 5.78 0.97 0.34
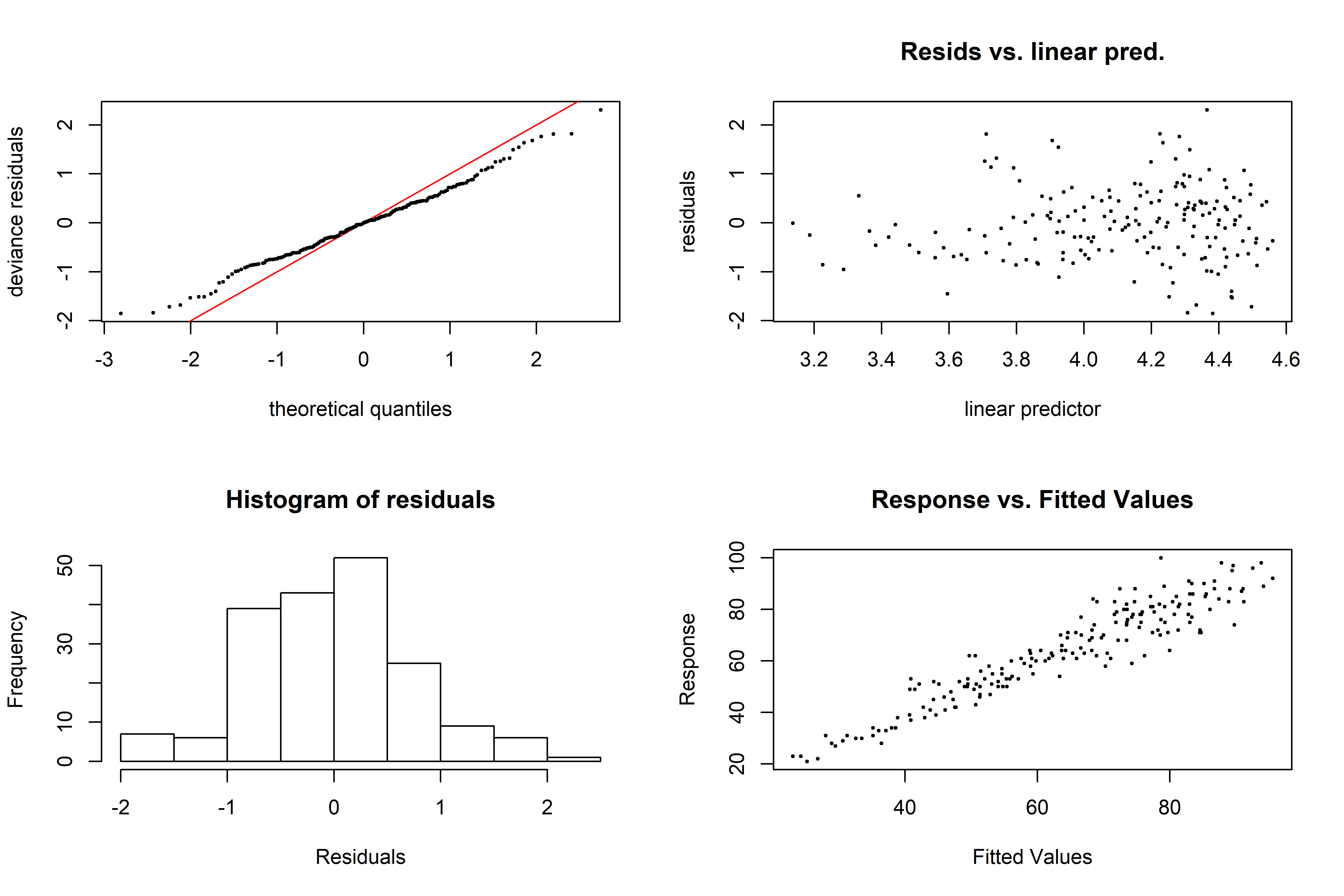
Les graphiques précédents n’indiquent aucune problématique majeure liée à :
- la linéarité et à la normalité des résidus,
- l’homogénéité de la variance.
Il est aussi fait état d’une convergence réussie de l’optimisation outer newton. Les valeurs de k utilisées pour ajuster les fonctions de lissage semblent adaptées (k-index≈1) avec des valeurs p non significatives.
La concurvité (l’équivalent non paramétrique de la colinéarité) se produit lorsqu’un effet fixe lissé peut être approximé par un ou plusieurs autres effets fixes lissés présents dans le modèle. Plus sa valeur est proche de 1, plus il y a de risques que le modèle soit difficilement interprétable ou que les estimés soient instables. Ici, les valeurs de concurvité sont proches de zéro.
para s(mois) s(annee)
worst 2.796979e-24 0.0161916883 0.016191688
observed 2.796979e-24 0.0007729336 0.003212910
estimate 2.796979e-24 0.0090339654 0.002737686
3.4 À propos de l’autocorrélation des résidus
L’une des hypothèses qui sous-tendent les modèles de régression linéaire est que les résidus ne sont pas corrélés, cela signifie que le résidu d’une observation n’affecte pas le résidu d’une autre observation. On dit alors que les résidus sont indépendants.
Cependant, quand on analyse une série temporelle avec un GAM, il peut y avoir une corrélation entre les résidus si la mesure d’un phénomène à un instant t est corrélée aux mesures précédentes (au temps t−1, t−n) ou aux mesures suivantes (à t+1, t+n).
Cette dépendance temporelle des résidus est appelée l’autocorrélation des résidus d’une série temporelle. Une série autocorrélée est ainsi corrélée à elle-même, avec un décalage (lag) donné.
On peut calculer l’autocorrélation des résidus d’une série temporelle pour différents décalages.
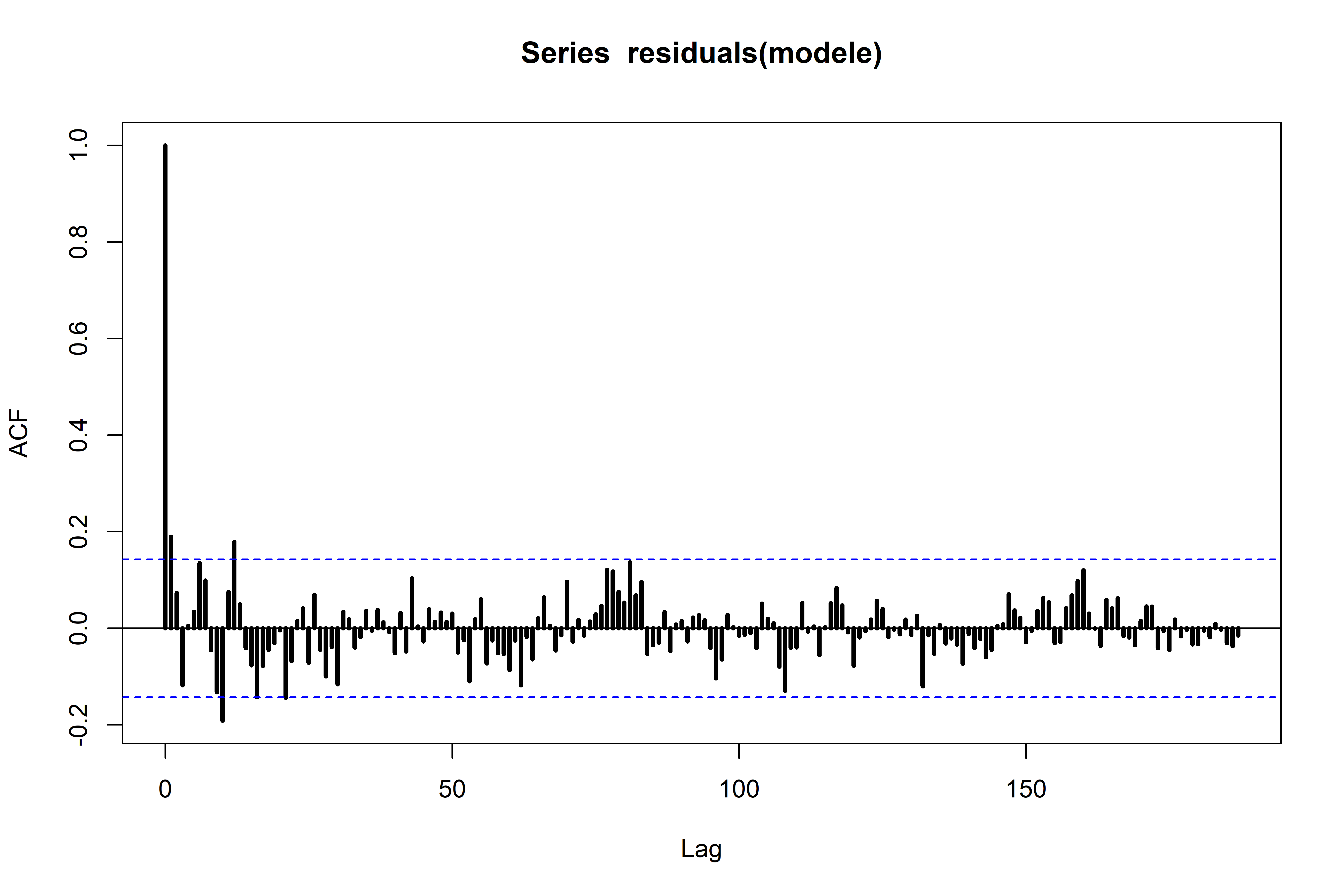
La fonction d’autocorrélation (ACF) des résidus peut être calculée et représentée sous la forme d’un corrélogramme.
Sur la figure suivante, seuls les 50 premiers décalages sont représentés.
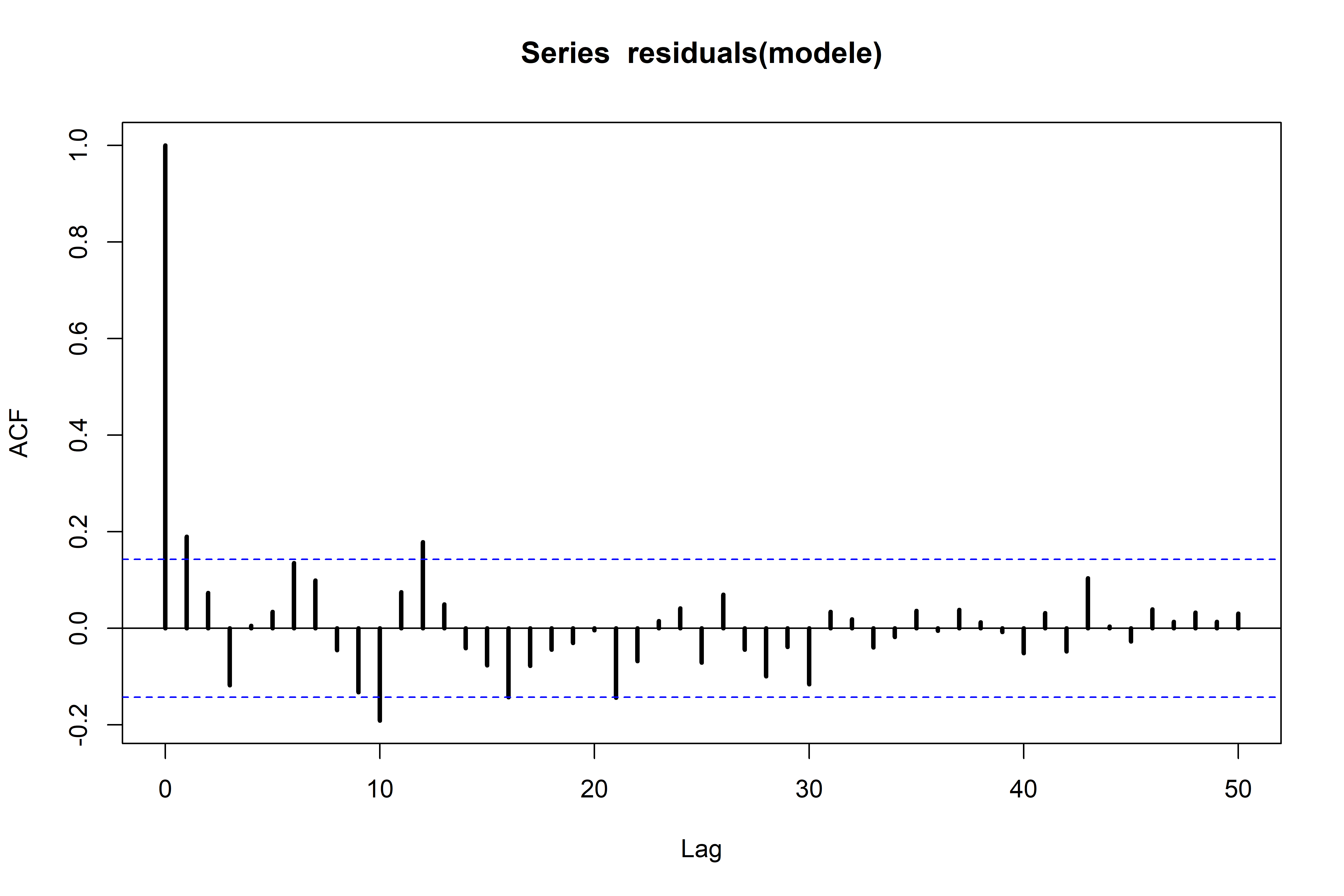
Sur un corrélogramme :
- le décalage pour lequel l’autocorrélation est calculée est indiqué sur l’axe des abscisses ;
- la valeur de la corrélation (entre -1 et 1) est indiquée sur l’axe des ordonnées ;
- les droites horizontales pointillées indiquent les seuils critiques au-delà desquels l’autocorrélation est considérée comme significative à 95 %.
Le pic au décalage 0 sur un tracé de l’ACF indique une corrélation positive parfaite (1) entre une observation de la série et elle-même (forcément !). Quelques rares pics de différents décalages excèdent les seuils critiques entre chaque observation et l’observation apparaissant xx mois avant ou xx mois après parmi les 188.
Cependant, le corrélogramme partiel n’illustre pas de corrélation particulièrement importante des résidus pour les 50 premiers décalages.
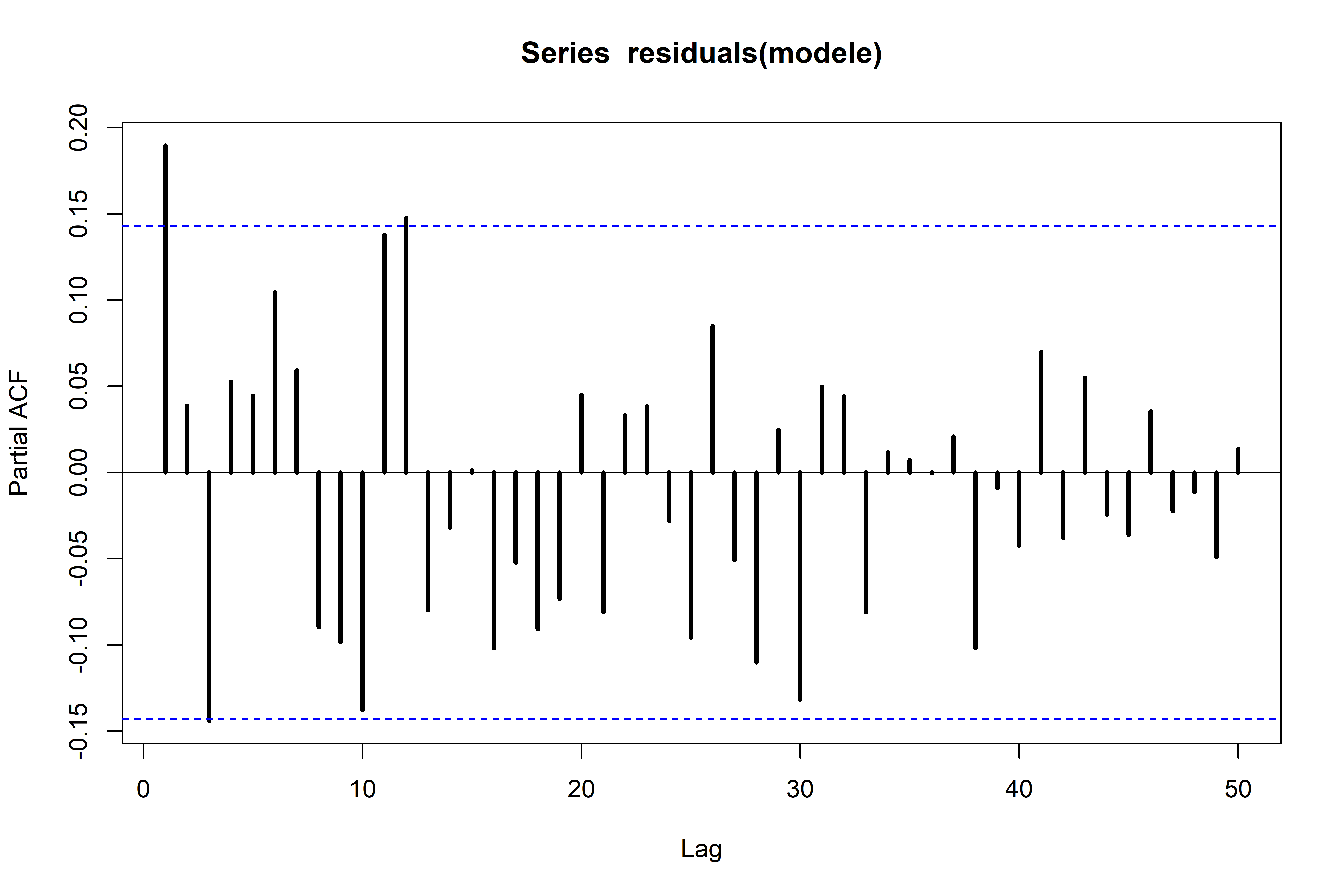
Les autocorrélations représentées ci-dessus sont empiriques et calculées à partir d’un échantillon de taille modeste (188 observations).
Quelques valeurs ACF sont en dehors des intervalles de confiance ce qui suggère une autocorrélation des résidus. Cependant, dans la cadre de cette première exploration, cette autocorrélation n’a pas été considérée.
3.5 Deux effets significatifs
Le nombre de hits du terme UQAC peut donc être expliqué par les deux effets fixes lissés mois et annee de façon statistiquement significative.
smooth.term report
1 s(mois) Chi.sq(10.307)=496.23; p<.001
2 s(annee) Chi.sq(5.775)=374.68; p<.001
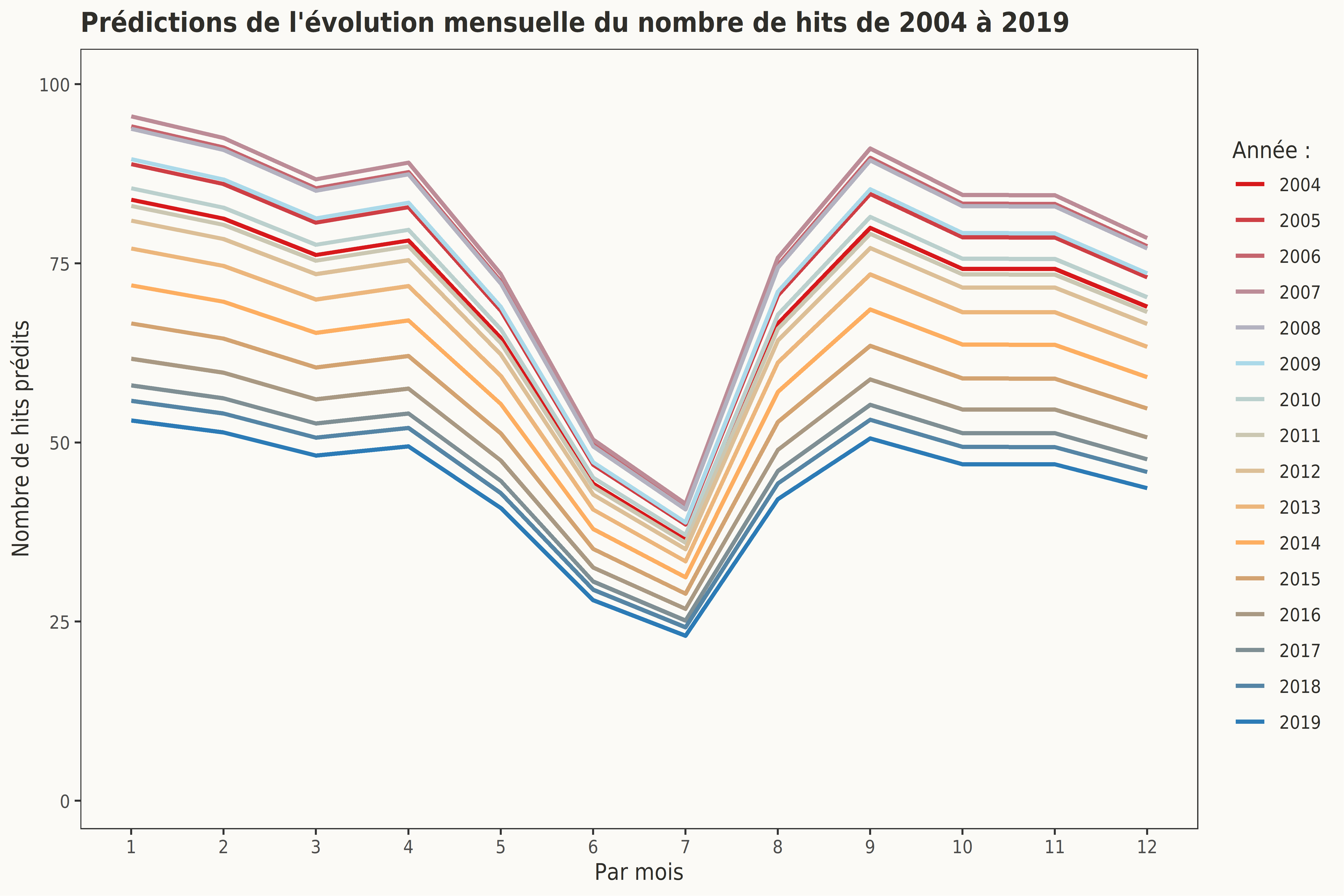
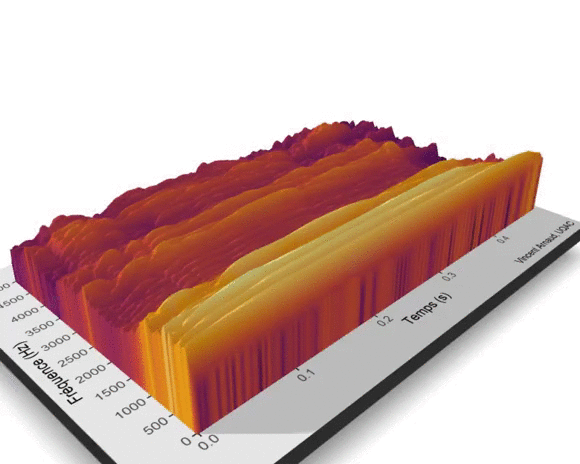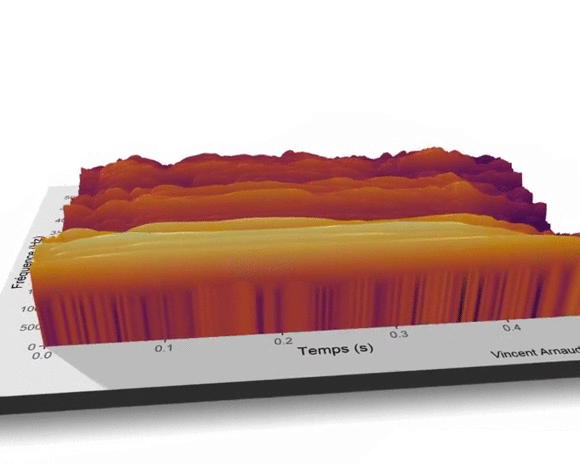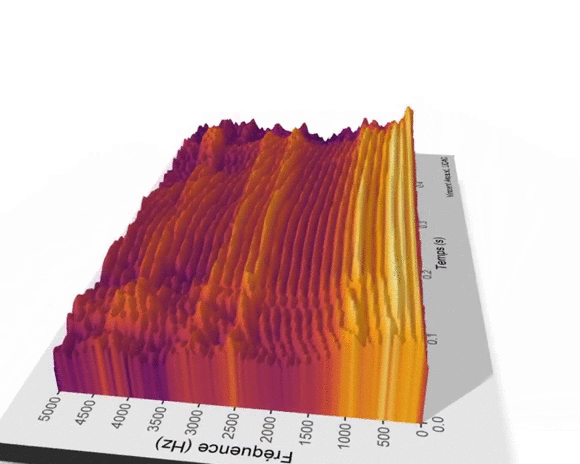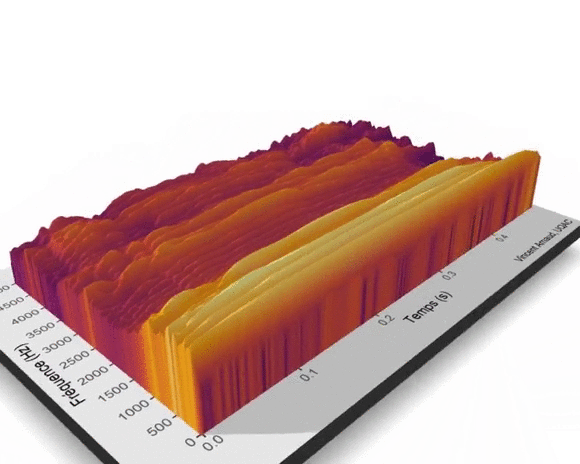
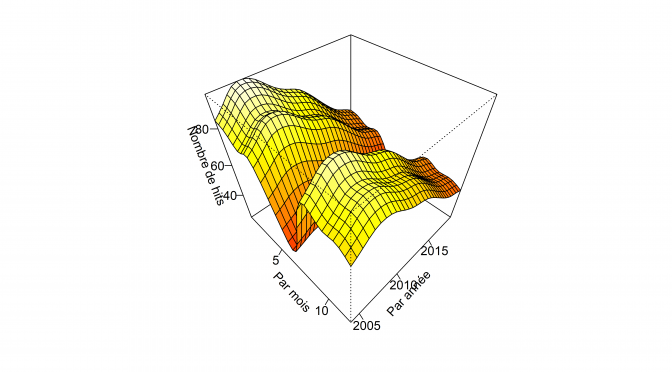
Le graphique suivant met en lumière un sommet du nombre de hits du terme UQAC en 2006-2007, et ce, quel que soit le mois considéré. À l’inverse, 2013 marque le début de la décroissance du terme UQAC. 2018 et 2019 sont les années au cours desquelles le terme UQAC a été le moins utilisé par les internautes dans leurs recherches sur le moteur de Google.
Ce graphique illustre aussi la relative stabilité de la popularité du terme UQAC entre janvier et avril et entre septembre et décembre et la chute du nombre de hits de cette requête entre mai et août, et ce, pour chacune des années entre 2004 et 2019. Depuis les années 2006-2007, les habitudes de consommation de l’information numérique ont changé et les supports de diffusion se sont diversifiés (Facebook, Twitter, YouTube…), cette décroissance des requêtes du terme UQAC peut être liée à cette diversification.
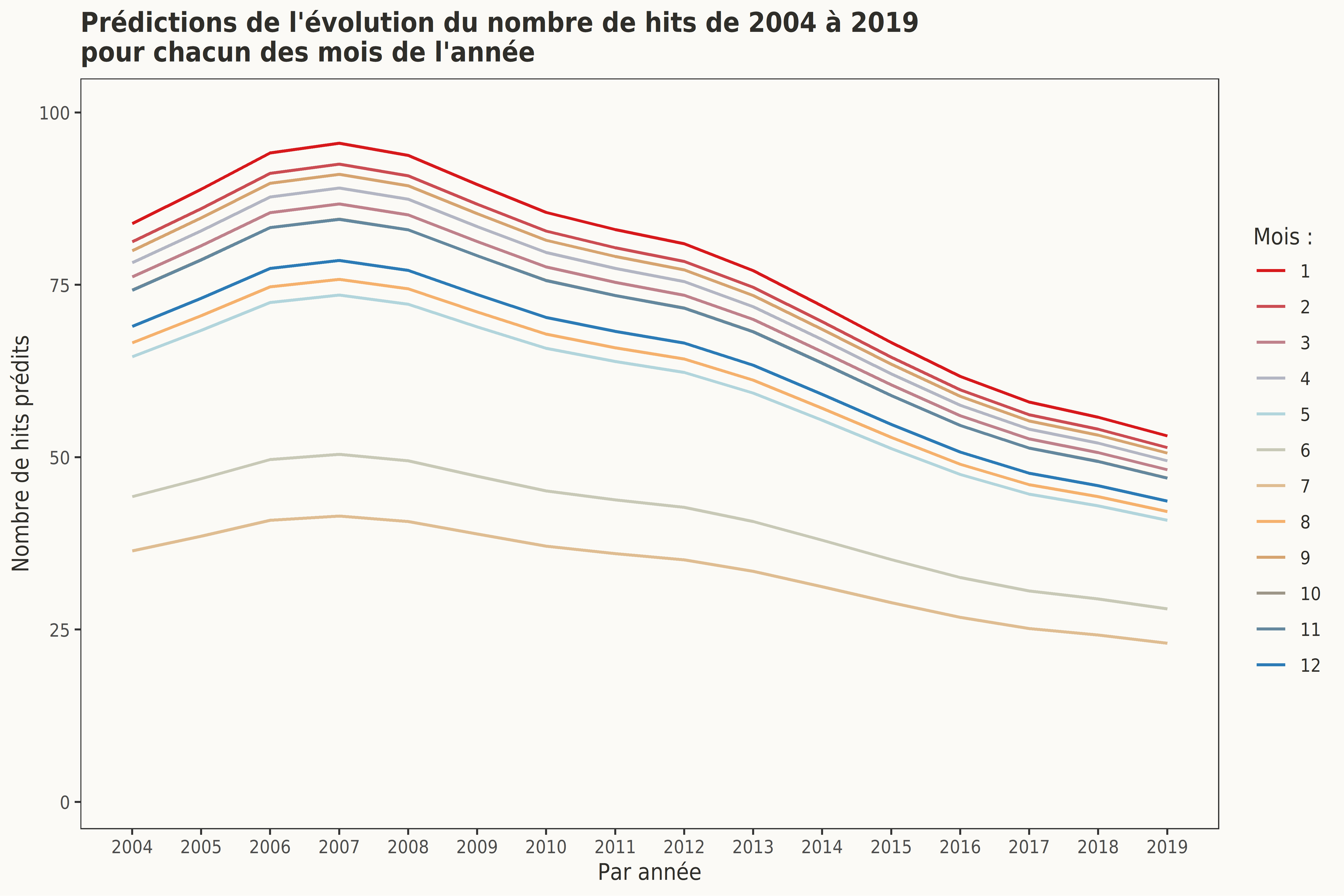
Ce second graphique, pendant du précédent, rend compte des mêmes tendances et notamment la chute drastique du nombre de hits durant les mois de juin et juillet de chacune des années de cet échantillon, mais aussi le nombre de requêtes le plus élevé du terme UQAC ont lieu durant le mois de janvier de chacune de ces années.
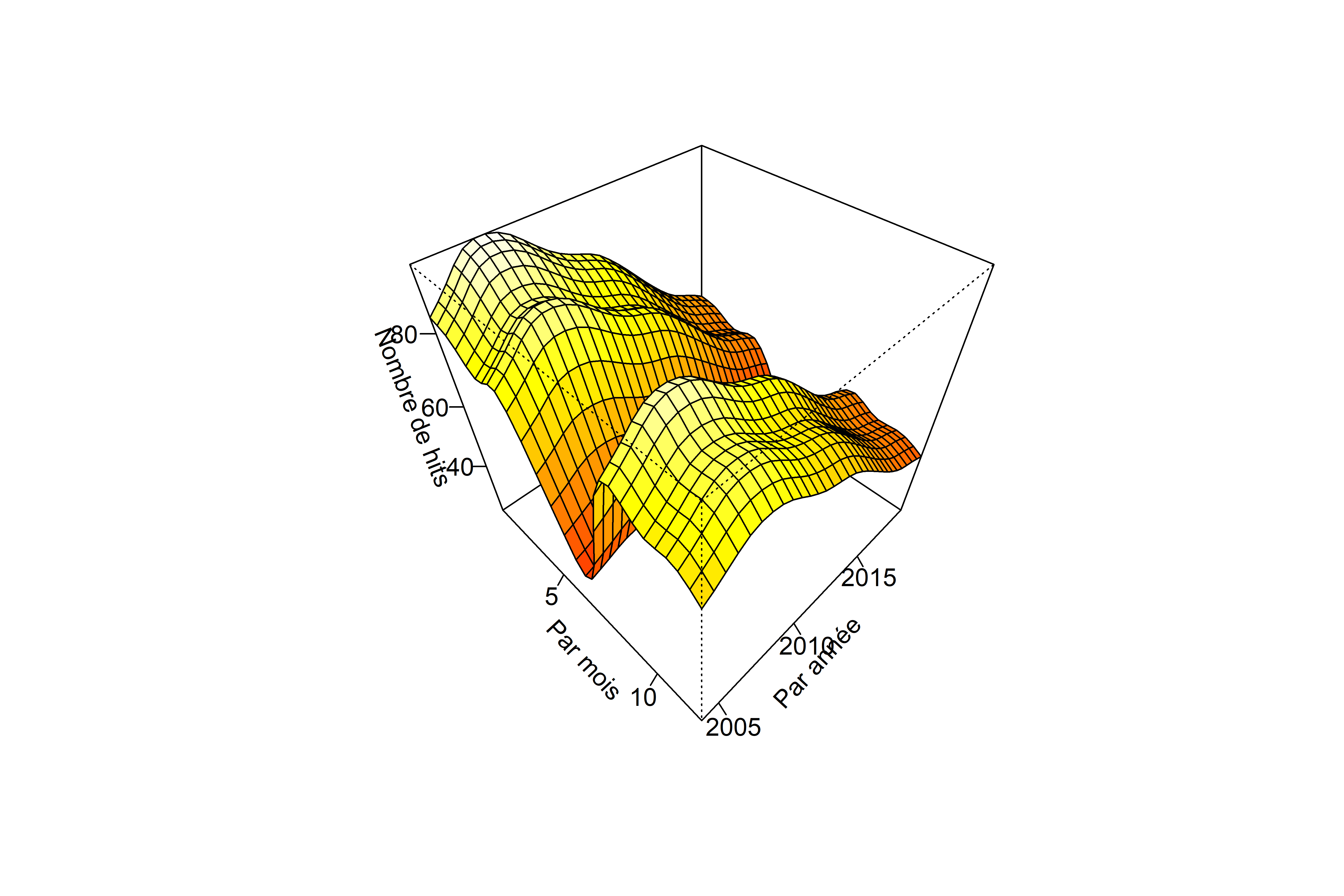
Il est aussi possible de visualiser en 3D la surface des valeurs prédites en fonction des deux effets fixes lissés mois et annee.
3.6 Ajustement du modèle
Le graphique suivant illustre l’ajustement des prédictions du modèle GAM aux données collectées. Rappelons qu’un ajustement exact des prédictions de ce modèle aux données collectées n’est pas recherché : il est d’ailleurs important d’éviter tout sur-ajustement.
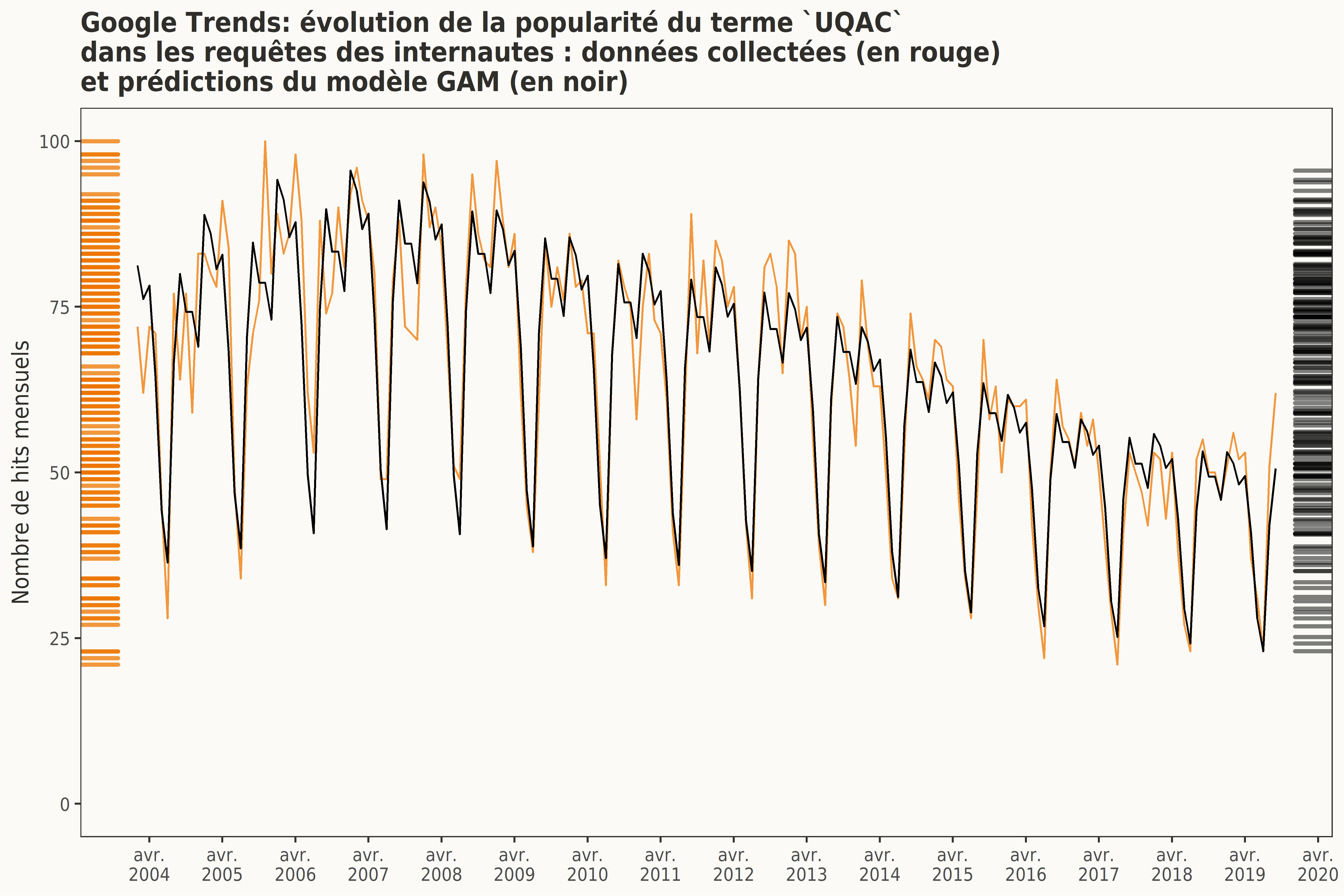
L’intérêt n’est ici que d’expliquer et modéliser la structure de la série temporelle. Cette modélisation n’a pas pour objectif de prévoir les valeurs futures de cette série temporelle.
4. Requêtes associées
Les internautes ayant recherché le terme UQAC ont également effectué d’autres requêtes. Google Trends offre la possibilité de récolter les plus fréquentes requêtes associées au terme UQAC utilisées par les internautes durant la période de 2004 à 2019 tout en fournissant également l’indice de popularité (le nombre de hits) de chacune de ces requêtes associées.
value keyword
1 uqac chicoutimi UQAC
2 chicoutimi UQAC
3 moodle UQAC
4 moodle uqac UQAC
5 uqac moodle UQAC
6 emploi uqac UQAC
7 uqam UQAC
8 pavillon sportif uqac UQAC
9 saguenay UQAC
10 uqac étudiant UQAC
11 uqac classiques UQAC
12 uqtr UQAC
13 bibliothèque uqac UQAC
14 bibliothèque UQAC
15 uqar UQAC
16 dossier étudiant uqac UQAC
17 accesd UQAC
18 uqac dossier étudiant UQAC
19 uqac portail UQAC
20 uqac dossier étudiant UQAC
21 ulaval UQAC
22 dossier étudiant UQAC
23 cegep chicoutimi UQAC
24 université laval UQAC
25 mage uqac UQAC
À partir de la liste de ces requêtes associées dont l’orthographe a été corrigée (notamment les accents), il est , par exemple, possible de calculer la fréquence des unigrammes et des bigrammes.
4.1 Fréquence des unigrammes
Les unigrammes ou mots typographiques sont traditionnellement définis comme des chaînes de caractères (string) comprises entre deux blancs typographiques ou entre un blanc typographique et un signe de ponctuation. Ils sont représentés ci-dessous sous la forme d’un nuage de mots (wordcloud). La taille de chaque forme sur le graphique suivant indique son effectif.

4.2 Fréquence des bigrammes
Les bigrammes sont les séquences de deux termes apparaissant de façon contiguë dans les requêtes associées.
Il est possible de représenter ces bigrammes sous la forme de graphes. Ces derniers sont principalement utilisés en mathématiques dans le cadre de la théorie des graphes. Un graphe est un ensemble de sommets (ou de noeuds, vertices en anglais) reliés deux à deux à deux par une ou plusieurs arêtes (ou arcs, edges en anglais).
Dans le graphe suivant, le degré de transparence représente l’effectif de chacun des bigrammes ainsi reliés. Le sens de la flèche rend compte de l’ordre d’apparition des termes dans chacun des bigrammes.
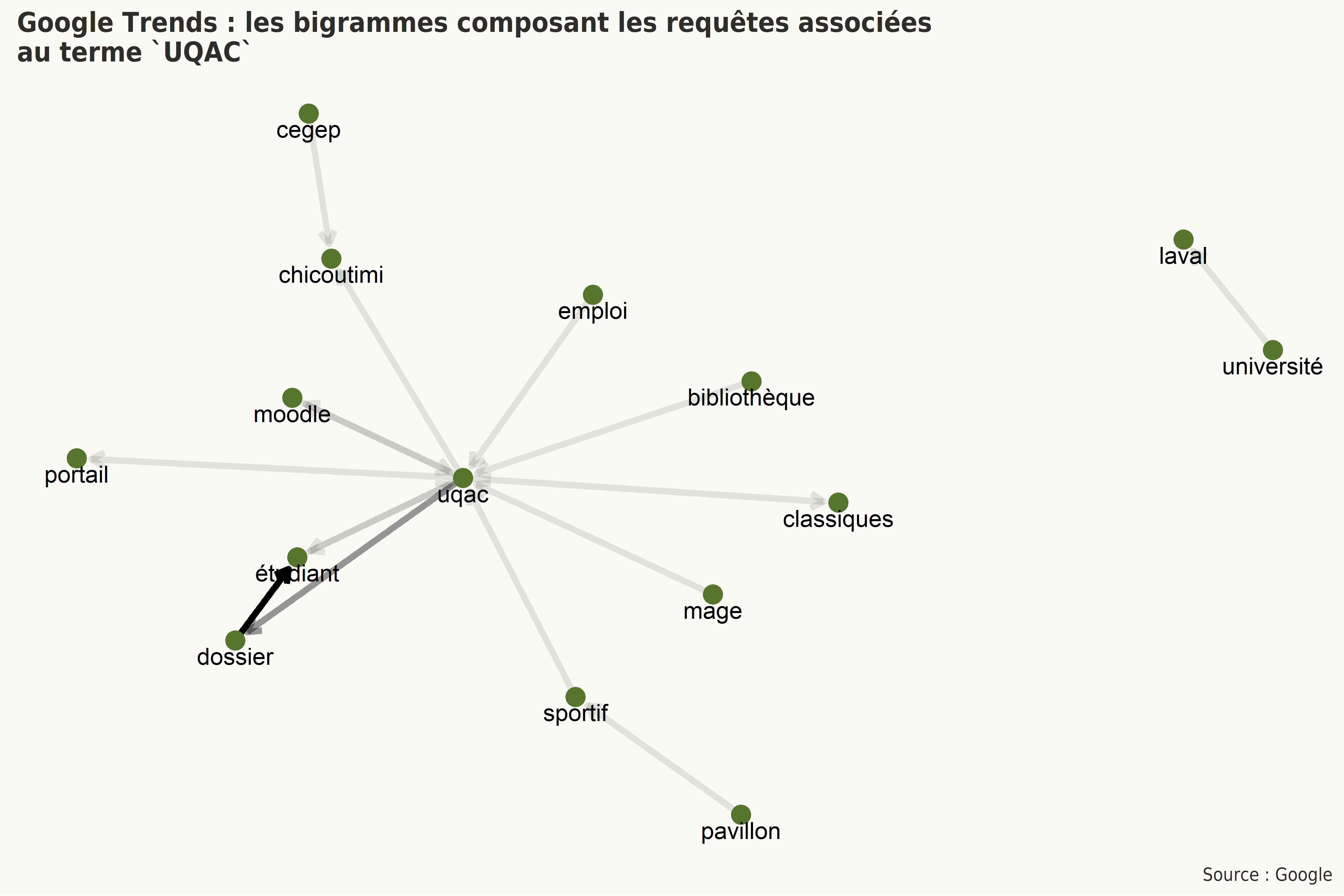
4.3 Interprétation sommaire
Le but n’est pas ici d’interpréter les résultats obtenus de façon détaillée, il est néanmoins intéressant de noter que les plus fréquentes requêtes associées au terme UQAC semblent concerner des aspects administratifs (Dossier étudiant, portail étudiant), financiers (emploi UQAC, Accès D) ou encore des liens généraux vers la bibliothèque, le pavillon sportif, Moodle, le MAGE-UQAC (les associations étudiantes). Ces requêtes semblent témoigner que le moteur de recherche de Google est majoritairement utilisé par les internautes comme un moteur de recherche interne à l’institution pour localiser rapidement des ressources d’usage régulier.
La seule requête populaire associée à la recherche concerne les Classiques en sciences sociales.
De façon plus générale, il est également intéressant de noter que les établissements d’enseignement associés à l’UQAC dans cette nébuleuse lexicale sont le Cégep de Chicoutimi (exclusivement), l’Université Laval (sous deux dénominations différentes), l’UQAR, l’UQTR et l’UQAM.
5. Origine géographique des internautes
Un dernier point, il semble évident que tout internaute ne connaissant pas cette université ne cherchera pas l’acronyme UQAC, mais sa dénomination complète.
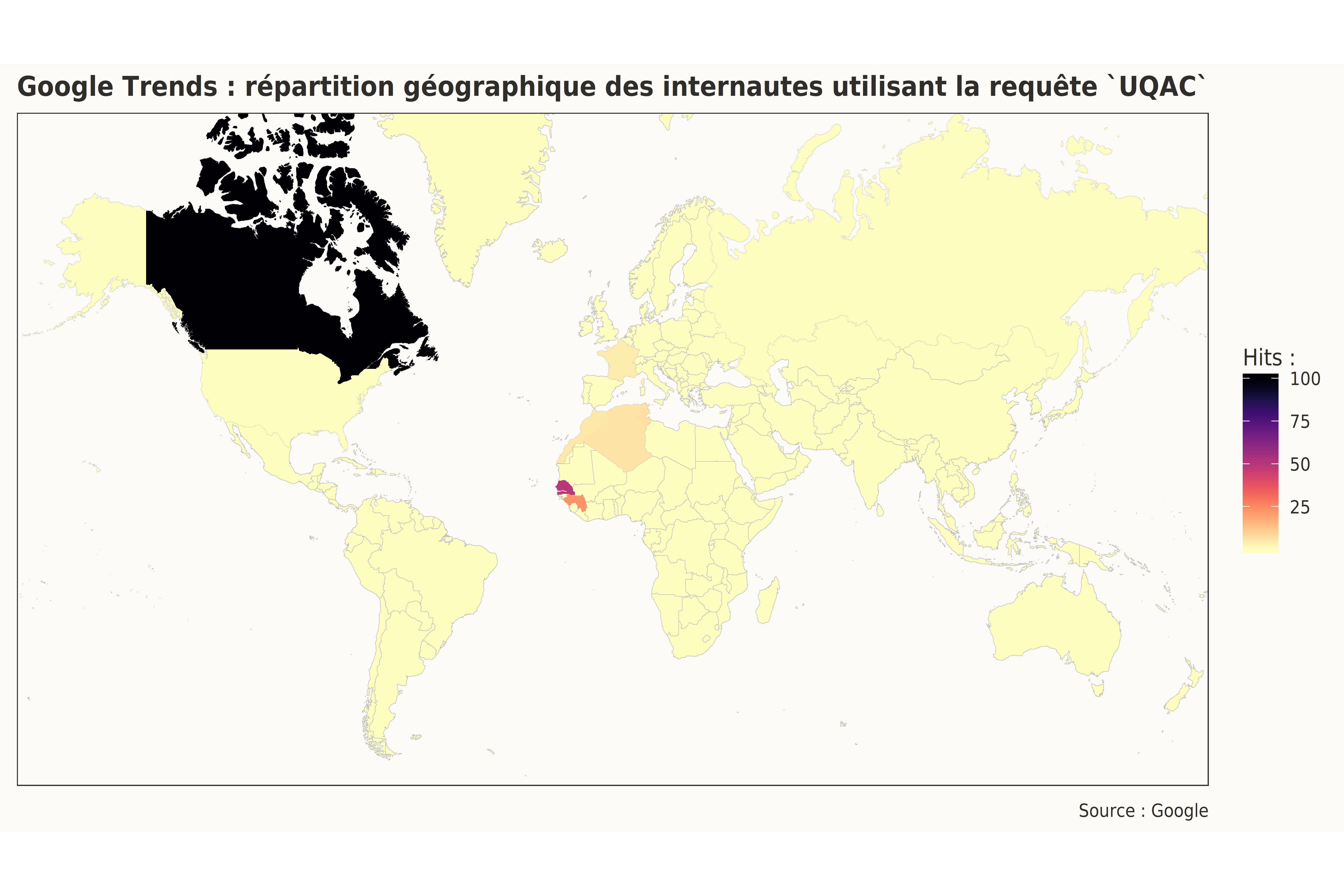
À cet égard, Google Trends offre la possibilité de colliger les zones géographiques où ce terme est populaire. On se rend ainsi rapidement compte que la requête UQAC provient essentiellement de la région du Saguenay–Lac-Saint-Jean, mais aussi de la Côte-Nord, mais très peu dans le reste du Québec et du Canada.
location hits
1 Saguenay 100
2 Alma 31
3 Roberval 26
4 Saint-Félicien 25
5 Dolbeau-Mistassini 23
6 Sept-Iles 16
7 Baie-Comeau 7
8 Québec City 2
9 Trois-Rivières 1
10 Levis 1
11 Montreal 1
12 Sherbrooke 1
13 Gatineau <1
14 Laval <1
15 Longueuil <1
16 Dakar <1
17 Ottawa <1
18 Toronto <1
19 Casablanca <1
20 Paris <1
Il est cependant intéressant de noter la relative popularité de cet acronyme en Guinée et au Sénégal, deux pays avec lesquels l’UQAC a possiblement des accords.
location hits
1 Canada 100
2 Senegal 50
3 Guinea 23
4 Tunisia 7
5 Algeria 6
6 Morocco 5
7 France 4
8 USA <1
9 Russia <1
6. Références
Coupé, C. (2018). Modeling linguistic variables with regression models: Addressing non-gaussian distributions, non-independent observations, and non-linear predictors with random effects and Generalized Additive Models for Location, Scale, and Shape. Frontiers in Psychology, 9. https://doi.org/10.3389/fpsyg.2018.00513
Sóskuthy, M. (2017). Generalised additive mixed models for dynamic analysis in linguistics : A practical introduction. http://arxiv.org/abs/1703.05339
Speelman, D. (2014). Logistic regression : A confirmatory technique for comparisons in corpus linguistics. In D. Glynn & J. A. Robinson (Éd.), Human Cognitive Processing (Vol. 43, p. 487‑533). Amsterdam: Benjamins.
Wood, S. N. (2017). Generalized additive models : An introduction with R (2nd ed.). Boca Raton: CRC Press.
7. Environnement
R version 3.6.1 (2019-07-05)
Plateforme : x86_64-w64-mingw32/x64 (64-bit)
Version du système d’exploitation : Windows 10 x64 (build 15063)
8. Bibliothèques utilisées
stats: The R Stats Package version 3.6.1
graphics: The R Graphics Package version 3.6.1
grDevices: The R Graphics Devices and Support for Colours and Fonts version 3.6.1
utils: The R Utils Package version 3.6.1
datasets: The R Datasets Package version 3.6.1
methods: Formal Methods and Classes version 3.6.1
base: The R Base Package version 3.6.1
mapproj: Map Projections version 1.2.6
maps: Draw Geographical Maps version 3.3.0
extrafont: Tools for using fonts version 0.17
ggwordcloud: A Word Cloud Geom for ‘ggplot2’ version 0.5.0
ggraph: An Implementation of Grammar of Graphics for Graphs and Networks version 2.0.0
igraph: Network Analysis and Visualization version 1.2.4.1
stringr: Simple, Consistent Wrappers for Common String Operations version 1.4.0
tidytext: Text Mining using ‘dplyr’, ‘ggplot2’, and Other Tidy Tools version 0.2.2
tidyr: Tidy Messy Data version 1.0.0
itsadug: Interpreting Time Series and Autocorrelated Data Using GAMMs version 2.3
plotfunctions: Various Functions to Facilitate Visualization of Data and Analysis version 1.3
sjPlot: Data Visualization for Statistics in Social Science version 2.7.2
mgcv: Mixed GAM Computation Vehicle with Automatic Smoothness Estimation version 1.8-28
nlme: Linear and Nonlinear Mixed Effects Models version 3.1-140
lubridate: Make Dealing with Dates a Little Easier version 1.7.4
gtrendsR: Perform and Display Google Trends Queries version 1.4.4
ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics version 3.2.1
PLoS Computational Biology Issue Image | Vol. 19(4) May 2023. (2023). PLOS Computational Biology, 19(4), ev19.i04. https://journals.plos.org/ploscompbiol/issue?id=10.1371/issue.pcbi.v19.i04









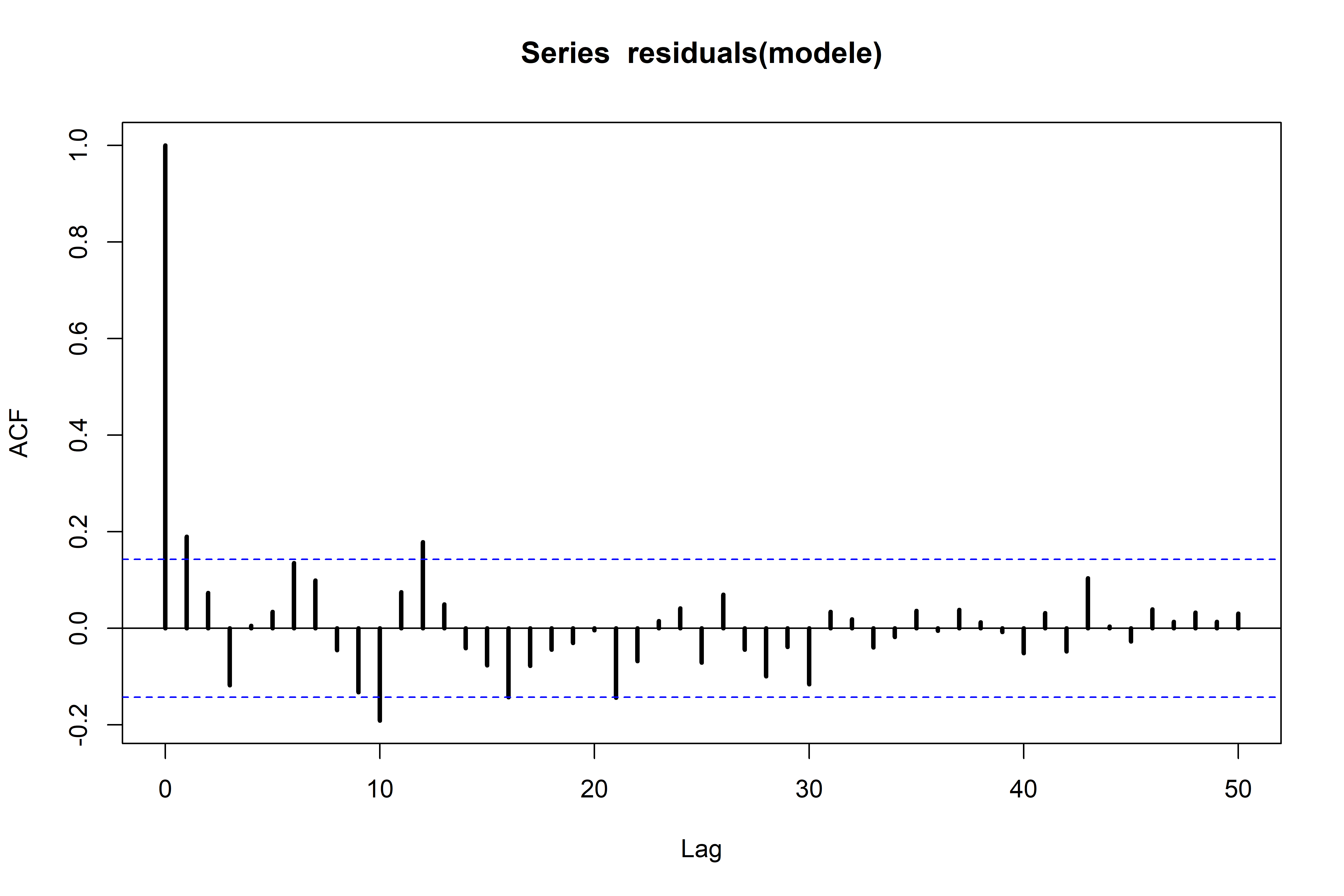
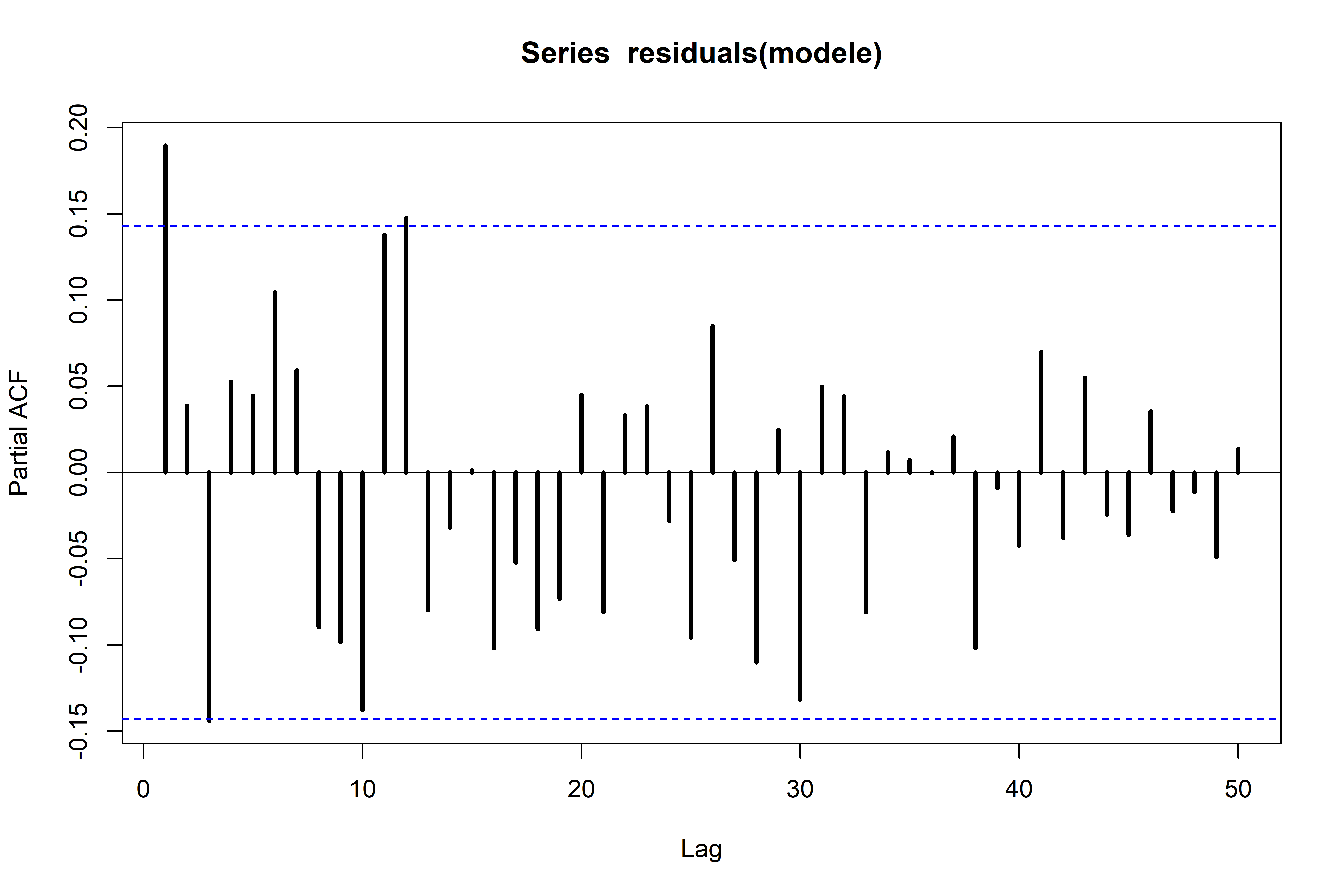









 Soucoupe Volante
Soucoupe Volante